Trie树 -- 高效的字典树

简介

Trie树是一种数据结构,它有一个好听的中文名字,叫"字典树".顾名思义,字典嘛,就是用来查单词的咯.因此Trie树的一大作用,就是在给定的字符串集合中(又称字典),查找给定的模式串(集合).相较于KMP算法,Trie树最大的特点在于,它是一种多对多的匹配算法,对于每一个给定的模式串,其效率可以压缩到O(n),是一种非常高效的算法.

原理

构造一棵Trie树

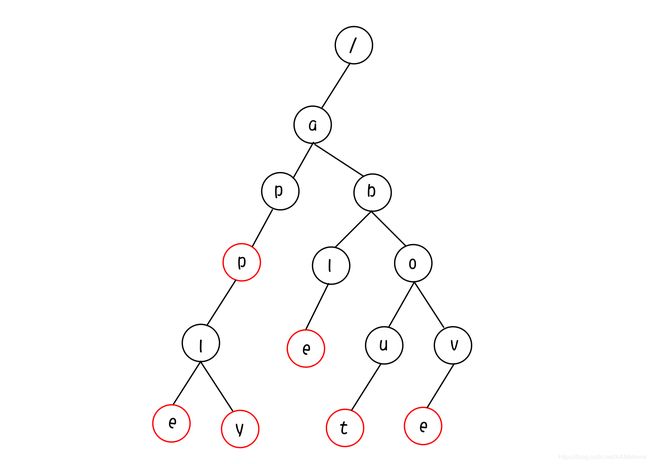
Trie树是一棵多叉树,而不是我们常用的二叉树,准确地说,它的最大分支数由字典的字符集含有的字符数决定,比如:若给定字典都是小写英文字母,则Trie树是一棵26叉树.至于为什么,我们画个图生成一下Trie树即可:

图1: 假设我们有一个字典为: apple,apply,app,那么Trie树应该长这样:

图2: 我们往字典里追加三个单词: able,about,above,那么Trie树就变成了这样:

图3: 我们往字典里追加不是以'a'开头的单词: be,beat,那么Trie树就变成了这样:

根据以上的图,我们可以总结Trie树的基本性质:

• 求一条公共路径,使得其覆盖的字符串尽可能多.
• 若无法将字符串全部字符都覆盖在这条公共路径中,则为多余的字符新建一条分支路径.
• 对于每一个字符串的结束,做一个标记.
• 根节点不包含任何字符.

将以上性质对应到我们的图中,不难发现:

• / 表示根节点,该节点不代表任何字符.
• 红圈表示一个字符串的结束,查询进行到红圈部分结束,则查询成功,否则失败.

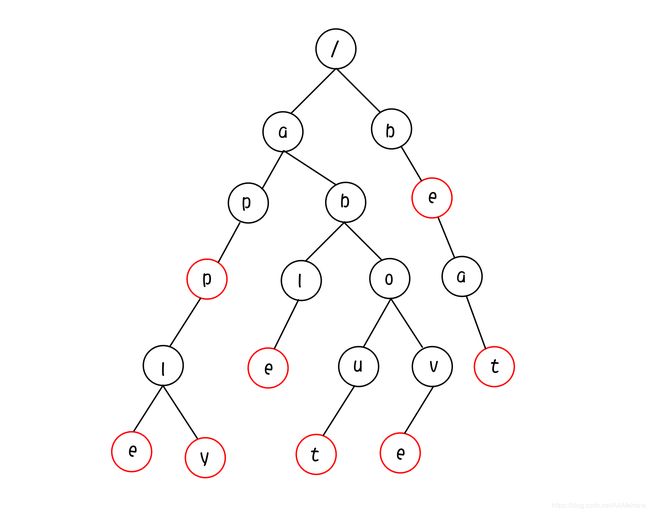
一般的Trie树可以这么画( / 表示根节点):

图4: 字符集含有n个字符,字符串数量不定的Trie树:

使用Trie树进行查询

对于图3中的Trie,我们查询以下集合的字符串: {“app”,“ab”,“back”},查询的过程和结果如下:

图5: 在Trie树中查询一个字符串集合{"app","ab","back"}的过程:

上图完全地涵盖了Trie查询可能出现的情况,一共有三种情况,两种状态:

• 情况一: 查询成功,如查询"app",沿着路径一路下来,每一个都匹配上,且正好字符串最后一个字符是结束标记.
• 情况二: 查询失败,如查询"ab",沿着路径一路下来,每一个都匹配上,但字符串最后一个字符不是结束标记.
• 情况三: 查询失败,如查询"back",沿着路径一路下来,在中途有字符无法匹配上(不在字典里),因而终止查询.

这就是说,要想在Trie树中查询成功,则应该同时满足两个条件:

1. 被匹配的字符串每一个字符都在字典中出现过.
2. 被匹配的字符串最后一个字符在字典中为结束标记.

实现

模拟(瞎暴力)实现

我们可以根据上面的原理,直接使用模拟的方式实现Trie树:

#include
#include
#define maxn 26         //字符集所含字符个数大小;
using namespace std;

struct Trie {
    char data;          //该位置的字符;
    int num;            //统计有多少单词经过该节点;
    Trie **son;       //该位置所有的子节点的根;
    bool isNull;        //判断此处是否为最后节点;
    Trie() {
        num = 1;
        son = new Trie*[26];
        for(int i = 0; i < maxn; i++)
            son[i] = nullptr;
        isNull = 0;
    }
    ~Trie() {
        for(int i = 0; i < maxn; i++) {
            delete[] son[i];
            son[i] = nullptr;
        }
        delete[] son;
        son = nullptr;
    }
};

void insertNode(Trie *&T,string str) {  //插入字典树;
    Trie *Temp = T;
    for(int i = 0; i < str.size(); i++) {
        int pos = str[i]-'a';
        if(!Temp->son[pos]) {       //不存在该分支,创建新分支;
            Temp->son[pos] = new Trie;
            Temp->son[pos]->data = str[i];
        }
        else Temp->num++;
        Temp = Temp->son[pos];
    }
    Temp->isNull = 1;
}

bool Trie_search(Trie *T,string str) {
    for(int i = 0; i < str.size(); i++) {
        int pos = str[i]-'a';
        if(!T->son[pos]) return 0;
        T = T->son[pos];
    }
    if(T->isNull)   return 1;   //此节点是单词结束,查找成功;
    return 0;
}

int main() {	//测试标程;
    int n;
    cin>>n;
    string str;
    Trie *T = new Trie;
    for(int i = 0; i < n; i++) {
        cin>>str;
        insertNode(T,str);
    }
    for(int i = 0; i < n; i++) {
        cin>>str;
        if(Trie_search(T,str))
            cout<<"Yes!"<<endl;
        else
            cout<<"No!"<<endl;
    }
    return 0;
}

显然,以上的实现是和原理一一对应的,其好处是代码实现好理解,但是相应的,也有以下不足之处:

• Trie树结构复杂,使用了双层指针,插入查询的实现涉及到指针,不易实现.
• 灵活度不高,不能很好地适应比赛千变万化的题目.

那么能不能对这种实现进行优化呢?答案是显然且必要的,下面我们来看看优化的算法.

空间优化

优化主要是对空间方面的优化,我们可以使用ACM(更加巧妙)的方式,来实现Trie树:

#include
#include
#include
using namespace std;

const int maxn = 2e+5;  //maxn近似为单词所有的结点数,尽可能开大;
int sc = 'a',cnt = 0,trie[maxn][26]; //字典树;
bool flag [maxn];   //判定是否是单词结束;

void init() {
    cnt = 0;
    memset(trie[0],0,sizeof trie[0]);
}

void insert_(string str) {
    int root = 0;
    for(int i = 0; i < str.size(); i++) {
        int id = str[i] - sc;
        if(!trie[root][id])
            trie[root][id] = ++cnt;
        root = trie[root][id];
    }
    flag[root] = true;
}

bool search_(string str) {
    int root = 0;
    for(int i = 0; i < str.size(); i++) {
        int id = str[i] - sc;
        if(!trie[root][id])
            return false;
        root = trie[root][id];
    }
    if(flag[root] == true)
        return true;
    return false;
}

int main() {	//测试标程;
    int n;
    init();
    cin>>n;
    string str;
    for(int i = 0; i < n; i++) {
        cin>>str;
        insert_(str);
    }
    for(int i = 0; i < n; i++) {
        cin>>str;
        if(search_(str)) cout<<"Yes!"<<endl;
        else cout<<"No!"<<endl;
    }
    return 0;
}

以上就是一个Trie树的模板,它和模拟实现的最大区别在于: 使用横向空间代替纵向空间,减少Trie树的层数.

上述模板是二维数组存储Trie树,其含义如下:

• Trie[][]第一维表示字符串的路径,按照路径可匹配一个字符串.
• Trie[][]第二维表示某个字符,即对于当前路径下,是否存在一个分支,包含该字符.

Trie[][]存储字符串时,其原理如下:

将字符串的每一个字符映射为对应的id,cnt用来记录当前插入到Trie树中的字符总数.

Trie[root][id]的值有两层含义:

1. 若Trie[root][id] > 0,则说明当前映射值为id的字符已经存在Trie树.
2. 在1成立的条件下,Trie[root][id]的值表示当前映射值为id的字符的下一个字符在Trie树中的位置.

依据上述原理,可以得到插入Trie树的算法:

1. 初始化root = 0,遍历字符串,对于其每一个字符,计算其映射值id,检查:
2. Trie[root][id] == 0是否成立,若成立,则进行插入,Trie[root][id] = ++cnt.
3. 若不成立,说明该位置已经有该字符,直接找到下一个字符应插入的位置: root = trie[root][id].
4. 重复上述步骤,直到字符串完全插入Trie树.

同理,可以得到从Trie树匹配字符串的算法:

1. 初始化root = 0,遍历字符串,对于其每一个字符,计算其映射值id,检查:
2. Trie[root][id] == 0是否成立,若成立,则说明Trie树当前路径不存在该字符,返回匹配失败.
3. 若成立,则说明当前路径存在该字符,找到下一个字符的位置: root = trie[root][id],重复2-3步.
4. 若顺利匹配完整个字符串,则应该检查字符串结束的位置在Trie树中是否是结束标志:
5. 若flag[root] == true成立,表明是结束标志,则返回匹配成功,否则返回匹配失败.

---

以上,就是Trie的入门讲解,有兴趣的话可以去其他地方看看进阶用法.