图的DFS和BFS算法解析

图是一种灵活的数据结构，一般作为一种模型用来定义对象之间的关系或联系。对象由顶点（V）表示，而对象之间的关系或者关联则通过图的边（E）来表示。

---

在图的基本算法中，最初需要接触的就是图的遍历算法，根据访问节点的顺序，可分为广度优先搜索（BFS）和深度优先搜索（DFS）。

本文将给出给出BFS和DFS的以下几种实现方式：
1、使用队列Queue实现图的BFS遍历
2、递归实现图的DFS遍历
3、使用栈Stack迭代实现图的DFS遍历

一、BFS（广度优先搜索算法）

BFS算法之所以叫做广度优先搜索，是因为它始终将已发现的顶点和未发现的之间的边界，沿其广度方向向外扩展。亦即，算法首先会发现和s距离为k的所有顶点，然后才会发现和s距离为k+1的其他顶点。

同深度优先搜索相反，BFS宽度优先搜索每次选择深度最浅的节点优先扩展。并且当问题有解时，宽度优先算法一定能够找到解，并且在单位耗散时间的情况下，可以保证找到最优解。

Java代码实现：

class Node1 {
    int x;
    Node1 next;
    public Node1(int x) {
        this.x = x;
        this.next = null;
    }
}
public class BFS {
    public Node1 first;
    public Node1 last;

    public static int run[] = new int[9];
    public static BFS head[] = new BFS[9];
    public final static int MAXSIZE = 10;
    static int[] queue = new int[MAXSIZE];
    static int front = -1;
    static int rear = -1;

    public static void enqueue(int value) {
        if(rear>=MAXSIZE) return;
        rear++;
        queue[rear] = value;
    }

    public static int dequeue() {
        if(front == rear) return -1;
        front++;
        return queue[front];
    }

    public static void bfs(int current) {
        Node1 tempNode1;
        enqueue(current);
        run[current] = 1;
        System.out.print("[" + current + "]");
        while (front != rear) {
            current = dequeue();
            tempNode1 = head[current].first;
            while (tempNode1 != null) {
                if(run[tempNode1.x] == 0) {
                    enqueue(tempNode1.x);
                    run[tempNode1.x] = 1;
                    System.out.print("[" + tempNode1.x + "]");
                }
                tempNode1 = tempNode1.next;
            }
        }
    }

    public boolean isEmpty() {
        return first == null;
    }

    public void print() {
        Node1 current = first;
        while(current != null) {
            System.out.print("[" + current.x + "]");
            current = current.next;
        }
        System.out.println();
    }
    public void insert(int x) {
        Node1 newNode1 = new Node1(x);
        if(this.isEmpty()) {
            first = newNode1;
            last = newNode1;
        }
        else {
            last.next = newNode1;
            last = newNode1;
        }
    }

    public static void main(String[] args) {
        int Data[][] = { {1,2}, {2,1}, {1,3}, {3,1}, {2,4}, {4,2},
                {2,5}, {5,2}, {3,6}, {6,3}, {3,7}, {7,3}, {4,5}, {5,4},
                {6,7}, {7,6}, {5,8}, {8,5}, {6,8}, {8,6} };
        int DataNum;
        int i,j;
        System.out.println("图形的邻接表内容为：");
        for(i=1;i<9;i++) {
            run[i] = 0;
            head[i] = new BFS();
            System.out.print("顶点" + i + "=>");
            for (j=0;j<20;j++) {
                if(Data[j][0] == i) {
                    DataNum = Data[j][1];
                    head[i].insert(DataNum);
                }
            }
            head[i].print();
        }
        System.out.println("深度优先遍历顶点：");
        bfs(1);
        System.out.println("");
    }

}

二、DFS（深度优先搜索算法）

DFS算法利用递归方式实现，和BFS不同的是BFS搜索产生的始终是一棵树，而DFS产生的可能会使一个森林。

对于深度优先搜索算法的思想。在一般情况下，当问题有解时，深度优先搜索不但不能够保证找到最优解，也不能保证找到解。如果问题状态空间有限，则可以保证找到解；但是当问题的状态空间无限时，则可能陷入“深渊”而找不到解。为此我们可以利用回溯算法中的思想，可以加上对搜索的深度限制。从而实现对于搜索深度的限制。当然深度限制设置必须合理，深度过深则影响搜索的效率，深度过浅时，则可能影响找到问题的解。

使用栈实现DFS思路关键点：

1、首先明确整个DFS主要便是对于栈进行操作，就是在顶点压栈和弹栈过程中我们需要进行的操作；

2、利用DFS的思想，深度遍历节点。直到栈内元素为空位置；

3、何时进行压栈：对于栈顶顶点，看其邻接顶点中是够存在未被遍历过得白色顶点，若有则对将其压栈，然后再对栈顶元素进行操作；

4、如果栈顶顶点的所有邻接顶点都是被遍历过的灰色顶点，则将栈顶元素弹栈，然后再对现在的栈顶元素进行操作；

5、算法结束时，所有元素均被遍历过即为灰色，并且栈已经为空。

DFS的思想是从一个顶点V0开始，沿着一条路一直走到底，如果发现不能到达目标解，那就返回到上一个节点，然后从另一条路开始走到底。
DFS适合此类题目：给定初始状态跟目标状态，要求判断从初始状态到目标状态是否有解

Java代码实现：

class Node {
    int x;
    Node next;
    public Node(int x) {
        this.x = x;
        this.next = null;
    }
}
public class DFS {
    public Node first;
    public Node last;

    public static int run[] = new int[9];
    public static DFS head[] = new DFS[9];

    public static void dfs(int current) {
        run[current] = 1;
        System.out.print("[" + current + "]");

        while (head[current].first != null) {
            if (run[head[current].first.x] == 0) { //如果顶点尚未遍历，就进行dfs递归
                dfs(head[current].first.x);
            }
            head[current].first = head[current].first.next;
        }
    }

    public boolean isEmpty() {
        return first == null;
    }

    public void print() {
        Node current = first;
        while (current != null) {
            System.out.print("[" + current.x + "]");
            current = current.next;
        }
        System.out.println();
    }

    public void insert(int x) {
        Node newNode = new Node(x);
        if (this.isEmpty()) {
            first = newNode;
            last = newNode;
        } else {
            last.next = newNode;
            last = newNode;
        }
    }

    public static void main(String[] args) {
        int Data[][] = {{1, 2}, {2, 1}, {1, 3}, {3, 1}, {2, 4}, {4, 2},
                {2, 5}, {5, 2}, {3, 6}, {6, 3}, {3, 7}, {7, 3}, {4, 5}, {5, 4},
                {6, 7}, {7, 6}, {5, 8}, {8, 5}, {6, 8}, {8, 6}};
        int DataNum;
        int i, j;
        System.out.println("图形的邻接表内容为：");
        for (i = 1; i < 9; i++) {
            run[i] = 0;
            head[i] = new DFS();
            System.out.print("顶点" + i + "=>");
            for (j = 0; j < 20; j++) {
                if (Data[j][0] == i) {
                    DataNum = Data[j][1];
                    head[i].insert(DataNum);
                }
            }
            head[i].print();
        }
        System.out.println("深度优先遍历顶点：");
        dfs(1);
        System.out.println("");
    }
}

图的两种存储方式：

要存储一个图，我们知道图既有结点，又有边，对于有权图来说，每条边上还带有权值。常用的图的存储结构主要有以下二种：

1.邻接矩阵

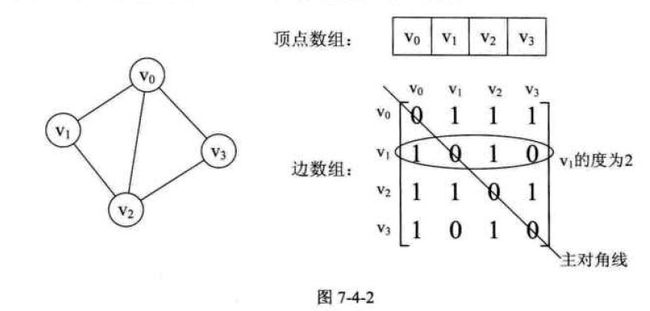
图的邻接矩阵（Adjacency Matrix)存储方式是用两个数组来表示图。一个一维的数组存储图中顶点信息，一个二维数组（称为邻接矩阵）存储图中的边或弧的信息。

设图G有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：
无向图：

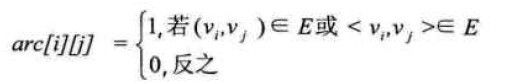
解释：若Vi和Vj之间有连接为1，没有连接为0

有向图：

在图的术语中，我们提到了网的概念，也就是每条边上都带有权的图叫做网。那些这些权值就需要保存下来。

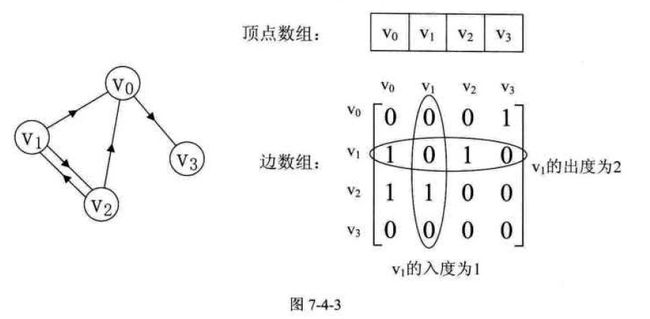
设图G是网图，有n个顶点，则邻接矩阵是一个n*n的方阵，定义为：

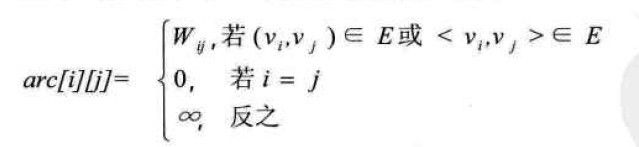
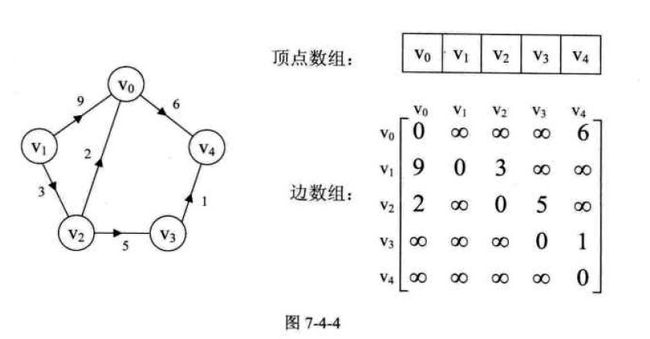
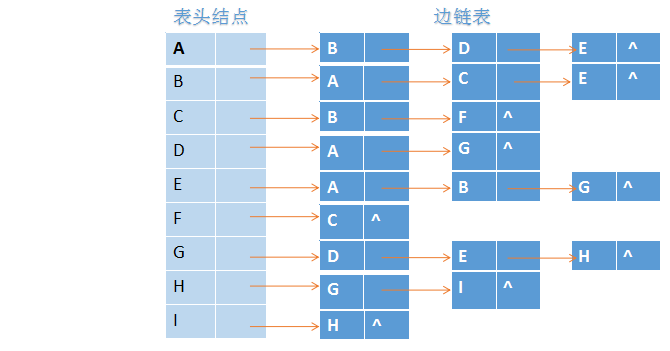
2.邻接表

邻接链表表示法对图中的每个顶点建立一个带头的边链表；第i条链表代表依附于顶点vivi所有边信息，若为有向图，则表示以顶点vivi为弧尾的边信息。邻接链接可以分为两部分，表头结点定义了顶点信息，随后的边链表表达了关于此顶点边信息。

所有表头结点以顺序结构的形式存储，以便可以随机访问任一顶点的边链表。上图的邻接链表表示法如下：