Top mAP and mAP

Top mAP and mAP

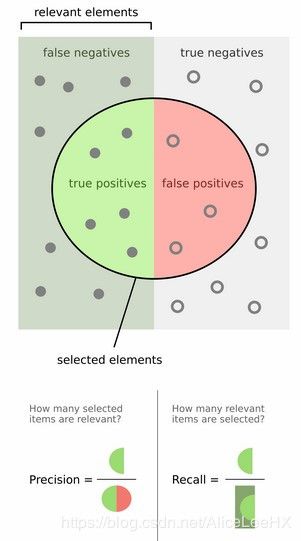
预备知识——Precision§ & Recall®

	Relevant	Non Relevant
Retrieved	True Positives (tp)	False Positives (fp)
Not Retrieved	False Negatives (fn)	True Negatives (tn)

则：
$$\begin{gathered} P=\frac{tp}{tp+fp} \\ R=\frac{tp}{tp+fn} \end{gathered}$$
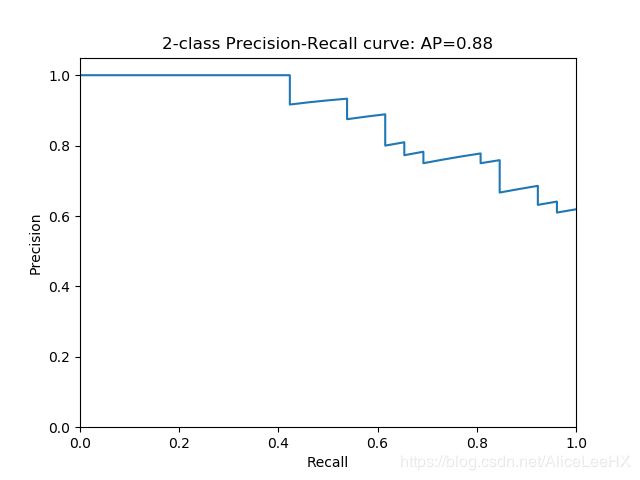
如下图所示，P和R的定义会更清楚一些：

• F1 Measurement：

  因为 $P$ 和 $R$ 是此消彼长的关系，在某些情况下，两者是矛盾的，因此为了综合考量两种因素，提出了F1 Measurement，其是Precision和Recall的加权调和平均：
  $$\begin{gathered} F=\frac{(a^2+1)P\ast R}{a^2(P+R)} \\ 当参数a=1时，就是常见的F_1: \\ {F}_1=\frac{2PR}{P+R} \end{gathered}$$
  $F_1$综合考量了 $P$ 和 $R$ 的结果，当$F_1$的结果比较高时，说明实验方法是比较理想的

• Average Precision:

  AP是为解决$P,R,F-measure$的单点值局限性的。为了得到一个能够反映全局性能的指标,其计算公式如下：
  $$AP={\int }_0^{1}P(R)dR$$
  也即：在准确率-召回率曲线中，曲线与坐标轴之间所形成的面积越大，代表性能越好，同时，在工业界，曲线应当尽可能向上突出

• mean Average Precision(mAP):

  对应于AP，mAP可以看作是AP在数据集上的平均值：
  $$\begin{gathered} mAP=\frac{{\sum }_{q=1}^{Q}AP(q)}{Q} \\ 其中Q是任务的数量 \end{gathered}$$

---

Example

Data

首先利用自己已经训练好的模型，得到所有测试样本的Confidence Score，假设共有20个测试样本，每个ID对应的Confidence Score 和Ground Truth Label如下表所示。

ID	Score	Label
1	0.23	0
2	0.76	1
3	0.01	0
4	0.91	1
5	0.13	0
6	0.45	0
7	0.12	1
8	0.03	0
9	0.38	1
10	0.11	0
11	0.03	0
12	0.09	0
13	0.65	0
14	0.07	0
15	0.12	0
16	0.24	1
17	0.1	0
18	0.23	0
19	0.46	0
20	0.08	1

对所有的Confidence Score进行排序，得到:

ID	Score	Label
4	0.91	1
2	0.76	1
13	0.65	0
19	0.46	0
6	0.45	0
9	0.38	1
16	0.24	1
1	0.23	0
18	0.23	0
5	0.13	0
7	0.12	1
15	0.12	0
10	0.11	0
17	0.1	0
12	0.09	0
20	0.08	1
14	0.07	0
8	0.03	0
11	0.03	0
3	0.01	0

Top-K mAP

如上表所示，我们根据Confidence的值对数据进行了排序，如果我们想得到Top-K的mAP的值的话，就按照降序原则，提取前K个数据作为样本，而不考虑后续的样本所得到的结果，如我们想得到Top-5的结果，所以其子数据集就是：

ID	Score	Label
4	0.91	1
2	0.76	1
13	0.65	0
19	0.46	0
6	0.45	0

在这个例子中，True Positives就是指第4和第2个样本，False Positives就是指第13，19，6个样本

$Precision=2/5=40$：对于某一二分类问题，我们选定了5个样本，其中正确的有2个，即准确率为40%；

$Recall=2/6=30$：意思是在Top-K和测试样本中，共有6个样本，但是因为我们只召回了2个，所以召回率为30%

而在实际多类别分类任务中，我们通常不满足只通过top-K来衡量一个模型的好坏，而是需要知道从top-1到top-N（N是所有测试样本个数）对应的precision和recall。而当K取N时，即为mAP。

Demo

此处，我们是随机生成的数据，同时利用欧几里得距离来生成Confidence

import numpy as np
import sklearn
import matplotlib.pyplot as plt
from sklearn.metrics import average_precision_score
from sklearn.metrics import precision_recall_curve

def dist(a,b):
    dists= np.sqrt(np.sum(np.square(a-b)))
    return dists

def compute_distances(Q,E):
    num=E.shape[0]
    connum=E.shape[1]
    dists=[]
    for i in range(num):
        sum=0
        for j in range(connum):
            sum=sum+dist(Q[j],E[i,j])
        dists.append(sum)
    dists=np.array(dists)
    return dists

def topmAP(Q,TX,FX,topk):

    ###     label       ###
    Tnum=TX.shape[0]
    Fnum=FX.shape[0]
    Ta=np.ones((Tnum))
    Fa=np.zeros((Fnum))
    y_true=np.hstack((Ta,Fa))

    ###     score       ###
    dTX=compute_distances(Q,TX)
    dFX=compute_distances(Q,FX)
    y_score=np.hstack((dTX,dFX))

    ###     rank        ###
    data=zip(y_true,y_score)
    data=sorted(data,key=lambda l:(l[1],l[0]))
    data_true=[]
    data_score=[]
    con=0
    ###         mAP        ###
    for _,i in enumerate(data):
        if con != topk:
            data_true.append(i[0])
            data_score.append(i[1])
            con=con+1

    data_true=np.array(data_true)
    data_score=np.array(data_score)
    
    resmAP=average_precision_score(data_true,data_score)

    return resmAP

def mAP(Q,TX,FX):
    tnum=TX.shape[0]
    fnum=FX.shape[0]
    num=tnum+fnum

    resmAP=topmAP(Q,TX,FX,num)

    return resmAP

if __name__ == "__main__":

    a = np.random.randn(10)
    b = np.random.randn(20,10)
    c = np.random.randn(10,10)
    
    topk=5

    topmap=topmAP(a,b,c,topk=topk)

    mapall=mAP(a,b,c)

    print('The Value of the Top-%d mAP is %f '%(topk,topmap))
    print('The Value of the mAP is %f '%(mapall))

• Result:

The Value of the Top-5 mAP is 0.700000
The Value of the mAP is 0.558517

显然随着我们选定的样本越来也多，recall一定会越来越高，而precision整体上会呈下降趋势。把recall当成横坐标，precision当成纵坐标，即可得到常用的precision-recall曲线。