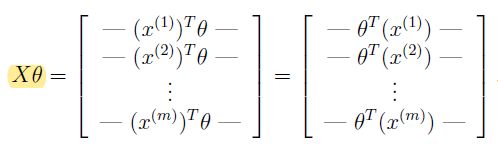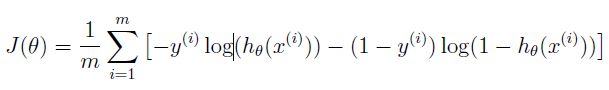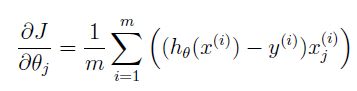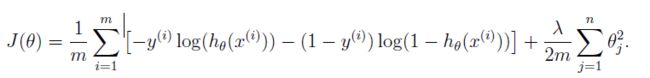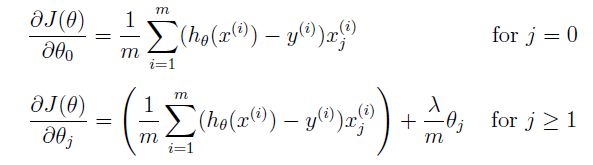吴恩达机器学习-——exercise3

Multi-class Classi cation and Neural Networks：

使用logistic回归和神经网络进行手写数字的识别分类（0-9）

已给脚本：

ex3.m - Octave/MATLAB 第一部分练习
ex3 nn.m - Octave/MATLAB 第二部分练习
ex3data1.mat - 手写数字的训练集
ex3weights.mat - 神经网络的初始quan'z
displayData.m - 数据可视化的函数
fmincg.m - 求解函数最优解的函数（类比fminunc）

编写脚本：

lrCostFunction.m - Logistic 回归的损失函数
oneVsAll.m - 训练一对多的分类器
predictOneVsAll.m - 预测一对多的分类
predict.m - 神经网络的预测函数

1 Multi-class Classi cation

1.1 Vectorizing the cost function:

使用logistic回归进行实现one-vs-all的分类：

训练集为5000个样本，每个样本有20pixel×20pixel共400个特征的图像信息

假设函数：

损失函数：

梯度：

正则化后的损失函数：

正则化后的梯度：

function [J, grad] = lrCostFunction(theta, X, y, lambda)
%LRCOSTFUNCTION Compute cost and gradient for logistic regression with 
%regularization
%   J = LRCOSTFUNCTION(theta, X, y, lambda) computes the cost of using
%   theta as the parameter for regularized logistic regression and the
%   gradient of the cost w.r.t. to the parameters. 

% Initialize some useful values
m = length(y); % number of training examples

% You need to return the following variables correctly 
J = 0;
grad = zeros(size(theta));

% ====================== YOUR CODE HERE ======================
% Instructions: Compute the cost of a particular choice of theta.
%               You should set J to the cost.
%               Compute the partial derivatives and set grad to the partial
%               derivatives of the cost w.r.t. each parameter in theta
%
% Hint: The computation of the cost function and gradients can be
%       efficiently vectorized. For example, consider the computation
%
%           sigmoid(X * theta)
%
%       Each row of the resulting matrix will contain the value of the
%       prediction for that example. You can make use of this to vectorize
%       the cost function and gradient computations. 
%
% Hint: When computing the gradient of the regularized cost function, 
%       there're many possible vectorized solutions, but one solution
%       looks like:
%           grad = (unregularized gradient for logistic regression)
%           temp = theta; 
%           temp(1) = 0;   % because we don't add anything for j = 0  
%           grad = grad + YOUR_CODE_HERE (using the temp variable)
%
%%
z = X * theta;
h = sigmoid(z); % 列向量m*1
J = ((y'*log(h))+(1-y')*log(1-h)) / (-m) + lambda*ones(size(theta'))*power(theta,2)/(2*m);

grad1 = ((h-y)'*X(:,1)) / m;
grad_other = ((h-y)'*X(:,2:end)) / m + lambda/m*theta(2:end)';
grad = [grad1 grad_other];
% =============================================================

grad = grad(:);

end

在第一次编写的时候出现了几个问题：

1. 对第一个参数也进行了正则化，实际是不需要的，所以第一个梯度值是不对的。所以进行了grad1 = ((h-y)'*X(:,1)) / m;这一步骤
2. 在进行求z的时候拘泥于公式，一直在套用theta'*X'的形式，最后换成了X*theta

1.2 one-vs-all :

function [all_theta] = oneVsAll(X, y, num_labels, lambda)
%ONEVSALL trains multiple logistic regression classifiers and returns all
%the classifiers in a matrix all_theta, where the i-th row of all_theta 
%corresponds to the classifier for label i
%   [all_theta] = ONEVSALL(X, y, num_labels, lambda) trains num_labels
%   logistic regression classifiers and returns each of these classifiers
%   in a matrix all_theta, where the i-th row of all_theta corresponds 
%   to the classifier for label i

% Some useful variables
m = size(X, 1);
n = size(X, 2);

% You need to return the following variables correctly 
all_theta = zeros(num_labels, n + 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];

% ====================== YOUR CODE HERE ======================
% Instructions: You should complete the following code to train num_labels
%               logistic regression classifiers with regularization
%               parameter lambda. 
%
% Hint: theta(:) will return a column vector.
%
% Hint: You can use y == c to obtain a vector of 1's and 0's that tell you
%       whether the ground truth is true/false for this class.
%
% Note: For this assignment, we recommend using fmincg to optimize the cost
%       function. It is okay to use a for-loop (for c = 1:num_labels) to
%       loop over the different classes.
%
%       fmincg works similarly to fminunc, but is more efficient when we
%       are dealing with large number of parameters.
%
% Example Code for fmincg:
%
%     % Set Initial theta
%     initial_theta = zeros(n + 1, 1);
%     
%     % Set options for fminunc
%     options = optimset('GradObj', 'on', 'MaxIter', 50);
% 
%     % Run fmincg to obtain the optimal theta
%     % This function will return theta and the cost 
%     [theta] = ...
%         fmincg (@(t)(lrCostFunction(t, X, (y == c), lambda)), ...
%                 initial_theta, options);
%
%%
options = optimset('GradObj', 'on', 'MaxIter', 50);

for iclass = 1:num_labels
    initial_theta = zeros(n+1, 1);
    [theta] = ...
        fmincg (@(t)(lrCostFunction(t, X, (y == iclass), lambda)), ...
        initial_theta, options);
    all_theta(iclass,:) = theta;
end

% =========================================================================
end

第一次的时候把事情想复杂了，想着先把训练集进行切片，然后分别训练模型，进行fmincg求最优化，得到每一种分类的theta，这种思路太过于复杂。

直接将y进行判断后传入lrCostFunction函数，然后将X的所有值传入即可，最后可得十种类别的401个特征的参数，然后可进行拟合函数，进而实行下一个测试集的判断

1.3 predictOneVsAll.m ：

通过上一个函数得到十种类别下的各种特征的参数，即一个10×401维数的矩阵

function p = predictOneVsAll(all_theta, X)
%PREDICT Predict the label for a trained one-vs-all classifier. The labels 
%are in the range 1..K, where K = size(all_theta, 1). 
%  p = PREDICTONEVSALL(all_theta, X) will return a vector of predictions
%  for each example in the matrix X. Note that X contains the examples in
%  rows. all_theta is a matrix where the i-th row is a trained logistic
%  regression theta vector for the i-th class. You should set p to a vector
%  of values from 1..K (e.g., p = [1; 3; 1; 2] predicts classes 1, 3, 1, 2
%  for 4 examples) 

m = size(X, 1);
num_labels = size(all_theta, 1);

% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

% Add ones to the X data matrix
X = [ones(m, 1) X];

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned logistic regression parameters (one-vs-all).
%               You should set p to a vector of predictions (from 1 to
%               num_labels).
%
% Hint: This code can be done all vectorized using the max function.
%       In particular, the max function can also return the index of the 
%       max element, for more information see 'help max'. If your examples 
%       are in rows, then, you can use max(A, [], 2) to obtain the max 
%       for each row.
%       
acc = X * all_theta';
[valu p] = max(acc, [], 2);
 

% =========================================================================
end

得到训练集的数据重新作为测试集来测试刚刚拟合的模型的准确率。

2  Neural Networks：

因为logistic回归只是一个线性分类器，所以不能得出较为复杂的假设函数，进而提出神经网络

神经网络适用于输入特征过于庞大的时候

2.1 predict.m：

function p = predict(Theta1, Theta2, X)
%PREDICT Predict the label of an input given a trained neural network
%   p = PREDICT(Theta1, Theta2, X) outputs the predicted label of X given the
%   trained weights of a neural network (Theta1, Theta2)

% Useful values
m = size(X, 1);
num_labels = size(Theta2, 1);
X = [ones(size(X,1),1) X];
% You need to return the following variables correctly 
p = zeros(size(X, 1), 1);

% ====================== YOUR CODE HERE ======================
% Instructions: Complete the following code to make predictions using
%               your learned neural network. You should set p to a 
%               vector containing labels between 1 to num_labels.
%
% Hint: The max function might come in useful. In particular, the max
%       function can also return the index of the max element, for more
%       information see 'help max'. If your examples are in rows, then, you
%       can use max(A, [], 2) to obtain the max for each row.
%
z2 = Theta1 * X';
a2_t = sigmoid(z2);
a2 = [ones(1,size(a2_t,2));a2_t];
z3 = Theta2 * a2;
h = sigmoid(z3');
[val, p] = max(h, [], 2);

% =========================================================================
end