回归分析（三）——多项式回归解决非线性问题

git源码：https://github.com/xuman-Amy/Regression-Analysis

【将线性回归模型转换为曲线——多项式回归】

之前都是将解释变量和目标值之间的关系假设为线性的，如果假设不成立，可以添加多项式选项，转换为多项式回归。

【sklearn实现多项式回归】

1、PoltnomialFeatures实现二项回归

# quadratic  二项回归
from sklearn.preprocessing import PolynomialFeatures
X = np.array([258.0, 270.0, 294.0, 
              320.0, 342.0, 368.0, 
              396.0, 446.0, 480.0, 586.0])\
             [:, np.newaxis]


y = np.array([236.4, 234.4, 252.8, 
              298.6, 314.2, 342.2, 
              360.8, 368.0, 391.2,
              390.8])
lr = LinearRegression()
pr = LinearRegression()
quadratic = PolynomialFeatures(degree=2) #二项式
X_quad = quadratic.fit_transform(X)

2、建立线性回归模型便于对比

# fit linear features
lr.fit(X, y)
X_fit = np.arange(250, 600, 10)[:, np.newaxis]
y_lin_fit = lr.predict(X_fit)

3、为多项式回归的transform特征fit 一个多变量回归模型

# fit quadratic features
pr.fit(X_quad, y )
y_quad_fit = pr.predict(quadratic.fit_transform(X_fit))

4、plot

#plot
plt.scatter(X,y, label = 'traing data')
plt.plot(X_fit, y_lin_fit, label = 'linear fit', linestyle = '--')
plt.plot(X_fit, y_quad_fit, label = 'quadratic fit')
plt.legend (loc = 'upper left')
plt.show()

 

5、模型评估

 

# MSE R^2
y_lin_pred = lr.predict(X)
y_quad_pred = pr.predict(X_quad)

print('Training MSE linear: %.3f, quadratic: %.3f' % (
        mean_squared_error(y, y_lin_pred),
        mean_squared_error(y, y_quad_pred)))
print('Training R^2 linear: %.3f, quadratic: %.3f' % (
        r2_score(y, y_lin_pred),
        r2_score(y, y_quad_pred)))

【housing data 建立非线性模型】

''# modeling nonlinear relationship in the housing dataset
X = df[['LSTAT']].values
y = df[['MEDV']].values

regr = LinearRegression()

#create quadratic and cubic features
quadratic = PolynomialFeatures(degree = 2)
cubic = PolynomialFeatures(degree = 3)
X_quad = quadratic.fit_transform(X)
X_cubic = cubic.fit_transform(X)

#fit features
X_fit = np.arange(X.min(), X.max(),1 )[:,np.newaxis]

#linear
regr = regr.fit(X, y)
y_lin_fit = regr.predict(X_fit)
linear_r2 = r2_score(y, regr.predict(X))

#quadratic
regr = regr.fit(X_quad, y)
y_quad_fit = regr.predict(quadratic.fit_transform(X_fit))
quadratic_r2 = r2_score(y, regr.predict(X_quad))

#cubic
regr = regr.fit(X_cubic, y)
y_cubic_fit = regr.predict(cubic.fit_transform(X_fit))
cubic_r2 = r2_score(y, regr.predict(X_cubic))

# plot results
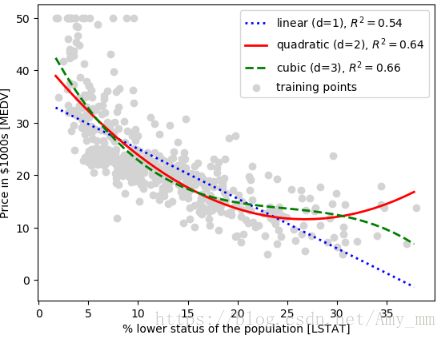
plt.scatter(X, y, label='training points', color='lightgray')

plt.plot(X_fit, y_lin_fit, 
         label='linear (d=1), $R^2=%.2f$' % linear_r2, 
         color='blue', 
         lw=2, 
         linestyle=':')

plt.plot(X_fit, y_quad_fit, 
         label='quadratic (d=2), $R^2=%.2f$' % quadratic_r2,
         color='red', 
         lw=2,
         linestyle='-')

plt.plot(X_fit, y_cubic_fit, 
         label='cubic (d=3), $R^2=%.2f$' % cubic_r2,
         color='green', 
         lw=2, 
         linestyle='--')

plt.xlabel('% lower status of the population [LSTAT]')
plt.ylabel('Price in $1000s [MEDV]')
plt.legend(loc='upper right')
plt.show()

 

图中可以看出三项式模型明显优于二项式和线性模型，但是三项式加大了模型的复杂度，容易导致过拟合。

 

在很多非线性问题中，可以考虑下log转换，将非线性问题变为线性问题。

      

在刚刚的问题中测试下log转换~~~

# log
#transform features
X_log = np.log(X)
y_sqrt = np.sqrt(y)

#fit features
X_fit = np.arange(X_log.min()-1, X_log.max()+1, 1)[:, np.newaxis]

#regr
regr = regr.fit(X_log, y_sqrt)
y_log_fit = regr.predict(X_fit)
linear_r2 = r2_score(y_sqrt, regr.predict(X_log))

# plot results
plt.scatter(X_log, y_sqrt, label='training points', color='lightgray')

plt.plot(X_fit, y_log_fit, 
         label='linear (d=1), $R^2=%.2f$' % linear_r2, 
         color='blue', 
         lw=2)

plt.xlabel('log(% lower status of the population [LSTAT])')
plt.ylabel('$\sqrt{Price \; in \; \$1000s \; [MEDV]}$')
plt.legend(loc='lower left')

plt.tight_layout()
#plt.savefig('images/10_12.png', dpi=300)
plt.show()

 = 0.69,比前文的三个回归模型都要精确啊~~~