示例程序:关于双目视觉,标定,立体匹配(视差算法),点云,双目三维重建的原理以及代码
Evision双目视觉
- 关于双目视觉的一些总结
- 相机模型
- 标定
- 视差算法:立体匹配
- 测量,三维重建
- 示例程序
- 参考文献
关于双目视觉的一些总结
笔者2013年进入吉林大学软件学院,2014年开始写自己的第一个完整的程序,期间受到过无数前辈的帮助,正是这个程序的完成给了我极大的信心,也让我喜欢上编程.这个程序是"基于OpenCV的双目测距",他的主要代码来自于邹宇华老师的OpenCV例程,我只不过进行了一些小小的修改,然后做了一个界面,在收获了许多经验的同时,也发现了双目视觉,乃至机器视觉的中文社区环境的一个问题,那就是有效资源非常少,很多人的博客只不过是互相转载,很多人提供的代码要么语焉不详,要么就是其他示例程序甚至是官方实例的修修补补,这对于初学者非常的不友好,一知半解的教程会让新手走很多弯路.在这期间,我的双目视觉程序仍然维持着更新,我决定把相关的资料全部公开,如果您发现错误,请及时留言评论,同时欢迎转载.文末附有程序代码链接,如果觉得有帮助,请加star,谢谢.
双目视觉程序: https://github.com/jiafeng5513/Evision
新版程序演示视频:https://www.bilibili.com/video/av46024738
旧版程序演示视频:https://www.bilibili.com/video/av8862669
相机模型
通常关于相机模型的文章只会提到小孔成像模型,这里要提醒的是,小孔成像模型并不能代表所有种类的相机,为了彻底搞清楚计算机视觉的基础,我们必须把相机模型弄明白.
1. 相机的投影模型
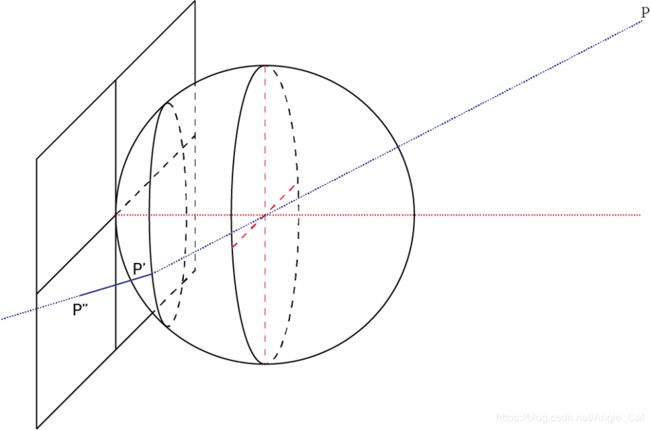
- 球面投影模型可以概括所有的相机模型,或者说所有的相机模型都是球面投影模型的一种特殊情况.
- 我们可以在光心和成像平面之间假想一个球面,物体先在球面上成像,再从球面上投影到成像平面上.
- 透镜的光学性质都是中心对称的,所以球面假设很合理.
- 穿过光心的光线是直线传播的,不同模型的角度差异的来源在于球面向平面投影的不同方法.
- 从球面向平面的投影,最常见的用处是绘制世界地图(可以百度:墨卡托投影,圆锥投影,等积投影等),
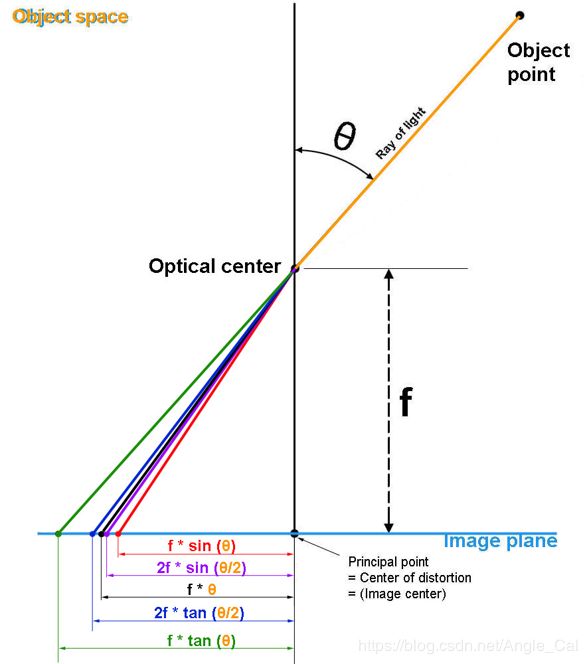
从球面向平面的投影有很多种方法,相机在制造时,镜头由很多片透镜组成,这些透镜的左右就是逼近某一种投影方法,使得透过镜头的光线直接透射在传感器平面上的情况等效于先投影在成像球面,再向成像平面投影,物体与光轴的夹角θ变化时,像点与图像中心的距离R也随之变化,按照变化关系的不同,经典相机模型被分为5类,其中透视投影模型又称为小孔模型.
| 计算公式 | 英文名 | 中文名 |
|---|---|---|
| R=f*tan(θ) | Perspective | 透射投影 |
| R=f*θ | Equidistant | 等距投影 |
| R=2fsin(θ/2) | Equisolid angle | 等立体角投影(等积投影) |
| R=f*sin(θ) | Orthographic | 正交投影 |
| R=2ftan(θ/2) | Stereographic | 球极投影(体视投影,保角投影) |
关于鱼眼镜头的投影特点,推荐大家看这篇知乎专栏,里面有一个视频直观的描述了这些投影的成像特点.
2. 不同类型的镜头
- 由于镜头制造上的限制,无法制造出满足理想情况的镜头,所以设计镜头时采用一个多项式逼近理想情况,其中K称为径向畸变系数.
- 由于实际镜头在拟合理想投影模型略有不同,这种性质是相机镜头的一种属性,用K描述.
- 径向畸变是最主要的畸变来源.此外,相机还有其他畸变,例如切向畸变,薄棱镜畸变,传感器倾斜畸变.
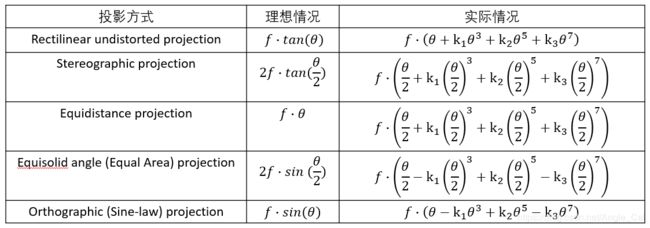
通过观察R和θ的曲线,我们能获知这些投影方式的一些性质:
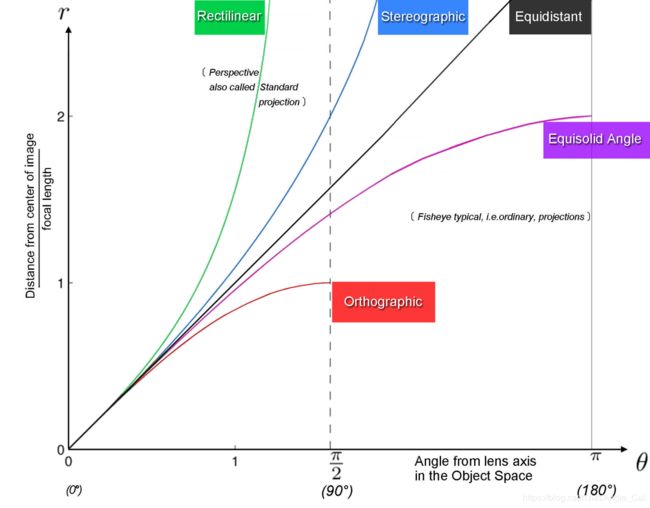
根据图像我们能得到一些结论: - 标准镜头(使用透射投影)的视角无法达到180°
- 鱼眼镜头能够实现180°的视角.
- 虽然理论上四种投影类型的鱼眼镜头都能实现180°视角,但是其最大视角对应的r是不同的,在传感器尺寸固定的情况下,不同的鱼眼相机实际能实现的最大视角不相同.
- 标准镜头在被摄物体到光心与光轴之间的夹角接近90°的过程中,单位角度变化所对应的成像点位移迅速增大,可以预见,图片边缘的情况一定和图片中心有所区别.
关于标准模型,这里提醒大家:
在一些涉及到相机模型的场景,要关注其中使用的相机模型是否符合预期,小孔模型使用的比较多,但是在使用广角相机和鱼眼相机时,小孔模型未必是有效的,此外在有些场景下,小孔模型过多的畸变系数可能会引起麻烦(例如训练深度神经网络时,过多的参数可能会引入复杂的可训练性的证明).
3. 小孔成像模型
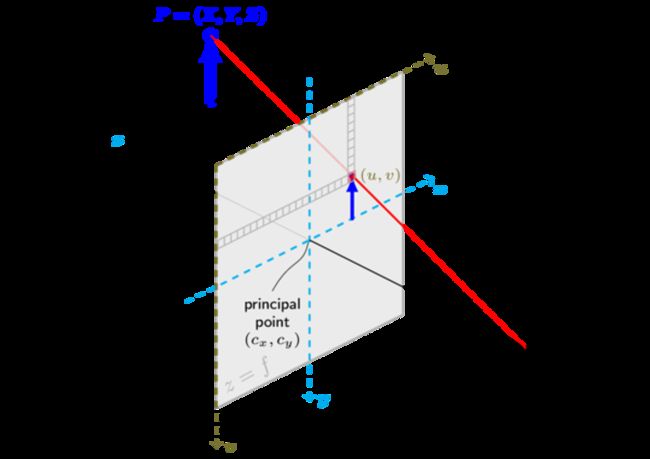
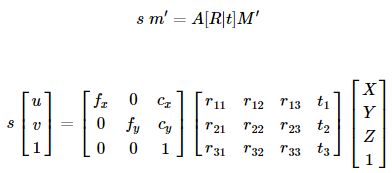
- (X,Y,Z) 是被摄物体的世界坐标
- (u,v) 是投影点在像素坐标系下的坐标
- A是相机矩阵,也叫内参矩阵,描述从相机坐标系到图像坐标系的变换
- (cx,cy)是主点坐标,通常位于图像中心
- fx,fy是以像素单位表示的焦距
- S是缩放系数
- [R|t] 也叫外参矩阵,描述由世界坐标系变换到相机坐标系
外参数把世界坐标变换到相机坐标,内参数把相机坐标变换到图像坐标
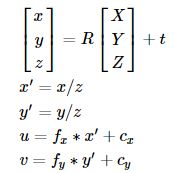
考虑一些畸变:
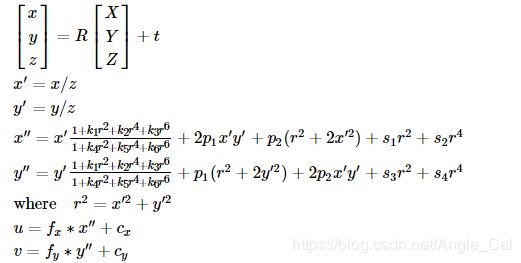
其中k是径向畸变系数,P是切向畸变系数,S是薄棱镜畸变系数,在大多数情况下,只考虑径向和切向畸变的低阶系数即可,在实验精度有限的前提下,使用高阶系数可能会引入很大的误差.此外,薄棱镜畸变和倾斜传感器畸变在大多数相机上都非常小

径向畸变K1的正负会影响畸变的视觉效果,负数时一般称为桶形畸变,正数时称为枕形畸变
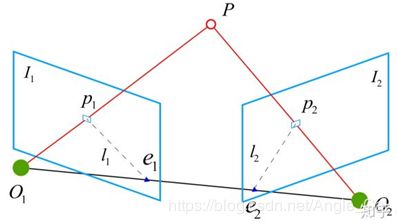
- 相机从两个位姿O1和O2拍摄同一个点P,分别成像p1和p2,这里p1和p2是相机坐标系下的坐标.PO1O2共面,两个位姿的成像面为
- I 1 I_1 I1和 I 2 I_2 I2,分别交平面 P O 1 O 2 PO_1O_2 PO1O2于交线 l 1 : p 1 e 1 l_1:p_1e_1 l1:p1e1和 l 2 : p 2 e 2 l_2:p_2e_2 l2:p2e2
- 把直线参数表示成: l = [ a b c ] T l=\begin{bmatrix}a & b & c\end{bmatrix}^{T} l=[abc]T
- 存在矩阵E,使得 E p 1 = l 2 Ep_1=l_2 Ep1=l2
- p 1 T l 1 = 0 , p 2 T l 2 = 0 p_{1}^{T}l_1=0,p_{2}^{T}l_2=0 p1Tl1=0,p2Tl2=0
- p 2 T E p 1 = 0 p_{2}^{T}Ep_1=0 p2TEp1=0
- 设 p 1 p_1 p1和 p 2 p_2 p2在图像坐标系下的坐标分别为 p 1 ′ p'_1 p1′和 p 2 ′ p'_2 p2′,K为相机矩阵
- K p 1 = p 1 ′ , K p 2 = p 2 ′ Kp_1= p'_1, Kp_2= p'_2 Kp1=p1′,Kp2=p2′.也就是 p 1 = K − 1 p 1 ′ , p 2 = K − 1 p 2 ′ p_1=K^{-1}p'_1, p_2=K^{-1}p'_2 p1=K−1p1′,p2=K−1p2′
- p 2 T E p 1 = 0 = ( K − 1 p 2 ′ ) T E K − 1 p 1 ′ = ( p 2 ′ ) T ( K − 1 ) T E K − 1 p 1 ′ p_2^{T} Ep_1=0=(K^{-1}p'_2)^{T}EK^{-1}p'_1=(p'_2)^{T}(K^{-1})^{T}EK^{-1}p'_1 p2TEp1=0=(K−1p2′)TEK−1p1′=(p2′)T(K−1)TEK−1p1′
- 令 ( K − 1 ) T E K − 1 = F (K^{-1})^{T}EK^{-1}=F (K−1)TEK−1=F,则有: ( p 2 ′ ) T F ( p 1 ′ ) = 0 (p'_2)^{T}F(p'_1)=0 (p2′)TF(p1′)=0
- 其中E为Essential Matrix(本质矩阵)
- F为Fundamental Matrix(基础矩阵)
- 本质矩阵和基础矩阵对于一对图片是固定值
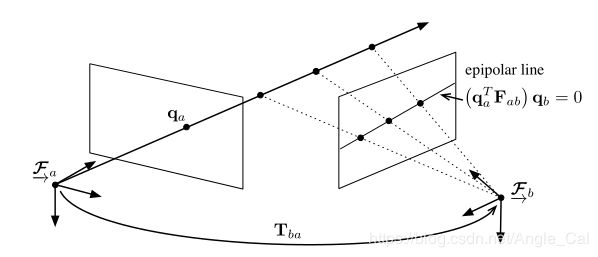
- 使用本质矩阵或者基础矩阵,可以从一个视角的一个像点确定另一个视角的一条线,所以这个性质被称为极限约束
- 从另一角度理解: P a c = O 1 P ⃗ P_{a}^{c}= \vec{O_1P} Pac=O1P
- 相机由 O 1 O_1 O1运行到 O 2 O_2 O2,相当于坐标系变换: T = O 1 O 2 ⟶ ⋅ P b c = O 2 P ⟶ = R P a c + t T=\stackrel{\longrightarrow}{O_1O_2}\cdot P_{b}^{c}= \stackrel{\longrightarrow}{O_2P}=RP_{a}^{c}+t T=O1O2⟶⋅Pbc=O2P⟶=RPac+t
- 由于空间中 O 1 O 2 P O_1O_2P O1O2P三点共面,所以 O 2 P ⟶ ⋅ ( O 1 O 2 ⟶ × O 1 P ⟶ ) = 0 \stackrel{\longrightarrow}{O_2P} \cdot(\stackrel{\longrightarrow}{O_1O_2}\times \stackrel{\longrightarrow}{O_1P})=0 O2P⟶⋅(O1O2⟶×O1P⟶)=0
- 在 O 2 O_2 O2的坐标系下可以表示为: P b c ⋅ ( T × ( R P a c ) ) = 0 P_{b}^{c} \cdot(T\times(RP_{a}^{c}))=0 Pbc⋅(T×(RPac))=0
5. 单应矩阵(Homography matrix)
- Homography matrix表达两个平面之间的投影关系,例如从三维空间中的实际平面到像平面,或者一个像平面到另一个像平面.
- 两张图片上的对应点的齐次坐标分别是(x’,y’,1)和(x,y,1),则有以下等式,其中H为单应矩阵:
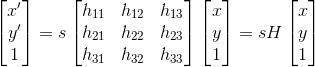
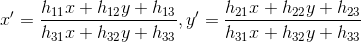
- 齐次化之后H中有8个自由量,至少需要8个方程也就是四对点来求解
- 实际平面到像平面的单应矩阵中包含了相机的内外参数和畸变
标定
相机的标定,目的是获取相机的参数和畸变系数,大致分为以下三类:
| 标定方法 | 优点 | 缺点 | 常用方法 |
|---|---|---|---|
| 传统相机标定法 | 可使用于任意的相机模型、 精度高 | 需要标定物 | Tsai两步法、张氏标定法 |
| 主动视觉相机标定法 | 不需要标定物、算法简单、鲁棒性高 | 成本高、设备昂贵 | 主动系统控制相机做特定运动 |
| 相机自标定法 | 灵活性强、可在线标定 | 精度低、鲁棒性差 | 分层逐步标定、基于Kruppa方程 |
视差算法:立体匹配
立体匹配算法也称为视差算法,目的是求解两幅图片之间的视差值.首先我们来定义视差值这个概念:
定义1:三维世界中有某一定点P,相机在两个位置对P成像,分别获取像点 p 1 p_1 p1和 p 2 p_2 p2,则称 p 1 p_1 p1和 p 2 p_2 p2为同名点
定义2:如果两张图片经过了畸变矫正,并且同名点的Y坐标在各自的像素坐标系下相等,我们称这两张图片为已校正图片对
定义3:在双目立体视觉中,两个相机的视角方向朝大致相同的方向,此时观察者站在相机的后方,视线方向与两台相机一致,他左手边的相机我们称之为 左相机,拍摄的图片称为 左视图
定义4:已校正图片对上,同名点的是X坐标之差,为视差值,逐像素计算式差值后组成的图片,称为 视差图 .特别地,在双目立体视觉中,以左视图为基准,通过同名点在右图上的坐标减去其在左图上的坐标得到的,称为左视差(图),相对应的称为右视差图
通过定义我们发现,立体匹配问题实际上是求同名点问题,因为只要找到准确的同名点,视差值不过是一个坐标差.可以说绝大多数视差算法的核心都是寻找同名点(一些基于深度学习的视差方法并不显式的求同名点).更具体点来说,当要求左视差图的时候,就是从左视图中依次取出每个像素,然后到右视图的某个范围内找 这个像素的同名点,这样当我们找完左视图上所有像素的同名点时,就得到了一张和左视图一样大的视差图了.
上面是通俗化的解释,接下来我们进行形式化的说明.视差算法是一个机器视觉的传统领域,经过多年的发展已经相当成熟,根据Schrstein和Szeliski的总结,双目立体匹配可划分为四个步骤:匹配代价计算、代价聚合、视差计算和视差优化。
-
匹配代价计算
匹配代价计算的目的是衡量待匹配像素与候选像素之间的相关性。两个像素无论是否为同名点,都可以通过匹配代价函数计算匹配代价,代价越小则说明相关性越大,是同名点的概率也越大。
每个像素在搜索同名点之前,往往会指定一个视差搜索范围D(Dmin ~ Dmax),视差搜索时将范围限定在D内,用一个大小为W×H×D(W为影像宽度,H为影像高度)的三维矩阵C来存储每个像素在视差范围内每个视差下的匹配代价值。矩阵C通常称为DSI(Disparity Space Image)。
匹配代价计算的方法有很多,传统的摄影测量中,使用灰度绝对值差(AD,Absolute Differences)[1]、灰度绝对值差之和(SAD,Sum of Absolute Differences)、归一化相关系数(NCC,Normalized Cross-correlation)等方法来计算两个像素的匹配代价;计算机视觉中,多使用互信息(MI,Mutual Information)法[2,3]、Census变换(CT,Census Transform)法[4,5]、Rank变换(RT, Rank Transform)法[6,7]、BT(Birchfield and Tomasi)法[8]等作为匹配代价的计算方法。不同的代价计算算法都有各自的特点,对各类数据的表现也不尽相同,选择合适的匹配代价计算函数是立体匹配中不可忽视的关键步骤。
无论是什么样的代价计算方法,都可以近似的看作这样的一个过程:首先在左图中确定一个像素或者一块像素区域,然后在右图中用某种形状的模板或者策略选定一块匹配区域,这个区域的大小和滑动步长都是超参数控制的,然后计算代价,移动模板窗口,再计算代价值,直到耗尽搜索范围,然后左图中选定第二块或者第二个像素,再重复这个过程。 -
代价聚合

代价聚合的根本目的是让代价值能够准确的反映像素之间的相关性。上一步匹配代价的计算往往只会考虑局部信息,通过两个像素邻域内一定大小的窗口内的像素信息来计算代价值,这很容易受到影像噪声的影响,而且当影像处于弱纹理或重复纹理区域,这个代价值极有可能无法准确的反映像素之间的相关性,直接表现就是真实同名点的代价值非最小。
而代价聚合则是建立邻接像素之间的联系,以一定的准则,如相邻像素应该具有连续的视差值,来对代价矩阵进行优化,这种优化往往是全局的,每个像素在某个视差下的新代价值都会根据其相邻像素在同一视差值或者附近视差值下的代价值来重新计算,得到新的DSI,用矩阵S来表示。
实际上代价聚合类似于一种视差传播步骤,信噪比高的区域匹配效果好,初始代价能够很好的反映相关性,可以更准确的得到最优视差值,通过代价聚合传播至信噪比低、匹配效果不好的区域,最终使所有影像的代价值都能够准确反映真实相关性。常用的代价聚合方法有扫描线法、动态规划法、SGM算法中的路径聚合法等。 -
视差计算
视差计算即通过代价聚合之后的代价矩阵S来确定每个像素的最优视差值,例如使用赢家通吃算法(WTA,Winner-Takes-All)来计算,如图2所示,即某个像素的所有视差下的代价值中,选择最小代价值所对应的视差作为最优视差。这一步非常简单,这意味着聚合代价矩阵S的值必须能够准确的反映像素之间的相关性,也表明上一步的代价聚合步骤是立体匹配中极为关键的步骤,直接决定了算法的准确性。
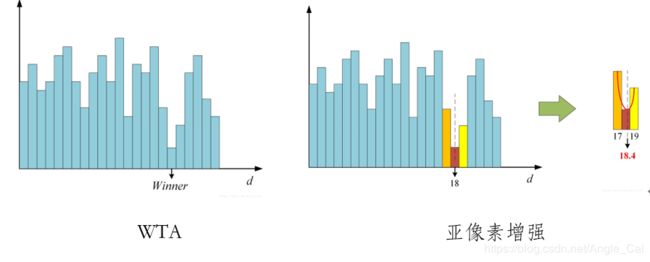
-
视差优化
视差优化的目的是对上一步得到的视差图进行进一步优化,是一些后处理方法的组合。改善视差图的质量,包括剔除错误视差、适当平滑以及子像素精度优化等步骤,一般采用左右一致性检查(Left-Right Check)算法剔除因为遮挡和噪声而导致的错误视差;采用剔除小连通区域算法来剔除孤立异常点;采用中值滤波(Median Filter)、双边滤波(Bilateral Filter)等平滑算法对视差图进行平滑;另外还有一些有效提高视差图质量的方法如鲁棒平面拟合(Robust Plane Fitting)、亮度一致性约束(Intensity Consistent)、局部一致性约束(Locally Consistent)等也常被使用。
由于WTA算法所得到的视差值是整像素精度,为了获得更高的子像素精度,需要对视差值进行进一步的子像素细化,常用的子像素细化方法是一元二次曲线拟合法,通过最优视差下的代价值以及左右两个视差下的代价值拟合一条一元二次曲线,取二次曲线的极小值点所代表的视差值为子像素视差值。如图3所示。
在编程实践中这里实际上最容易出现问题。OpenCV实现的BM和SGBM并没有亚像素增强的步骤,所以它输出的视差数据是CV8U也就是unsingned char类型的,他的视差等级非常有限,比如说设置的最大视差是50,那他的视差就是0-49这50个整数,精度就很差了;如果进行亚像素增强,输出的数据格式就是float或者double的,这是不能直接在屏幕上显示的,必须要进行归一化,所以如果视差数据只是整个程序的中间结果,那么就不可以保存成图片再读取,这样就会损失精度。 -
代价函数
代价函数的想法是,确定了同名点实际上视差就确定了,那么我们输入左点和视差,在给定的视差范围内计算代价值,代价最低的那个情况就最可能是同名点,此时的视差也最可信.下面列举几种常见的代价函数:
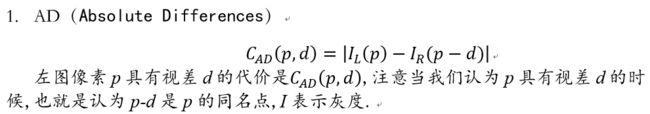

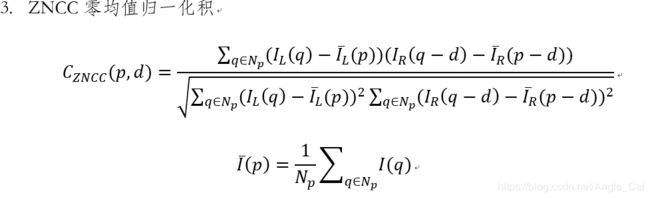
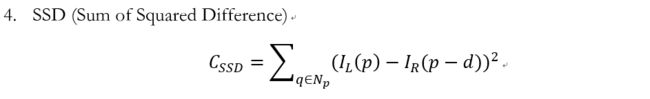

-
OpenCV-BM
OpenCV-BM算法使用SAD作为代价函数,在源码中我们看到该方法被称为“基于SAD的快速立体匹配算法”.根据对源码的解析,我把OpenCV-BM的流程分为四个部分:校验、预处理、视差计算和后处理.
校验:校验算法的输入和超参数的选取是否合理.左右视图大小相等,格式均为CV_8UC1,接收视差图的Mat为CV_16SC1或者CV_32FC1, preFilterSize是[5,255]之间的奇数, preFilterCap在[1,63], SADWindowSize是[5,255]之间的奇数且不能大于图片的宽或高, numDisparities必须能被16整除, textureThreshold必须是非负数, uniquenessRatio必须是非负数.
| 超参数 | 说明 | |
|---|---|---|
| 1 | preFilterType | 前处理可以是NORMALIZED或XSOBEL |
| 2 | preFilterSize | 归一化窗口大小,对于XSobel没有意义 |
| 3 | preFilterCap | 截断值.对于XSobel(X方向上的Sobel),如果滤波后结果在[-prefilterCap,preFilterCap]之间,对应取[0, 2*preFilterCap] |
| 4 | SADWindowSize | SAD窗口大小 |
| 5 | minDisparity | 视差搜索起点 |
| 6 | numDisparities | 视差窗口,一个推荐值是((width / 8) + 15) & (~0xfl) |
| 7 | textureThreshold | 低纹理区域的判断阈值. 如果当前 SAD 窗口内所有邻居像素点的 x-导数绝对值之和小于指定阈值,则意味着当前窗口内的图像变化率太低也就是纹理很差,则该窗口对应的像素点的视差值设为0. |
| 8 | uniquenessRatio | 视差唯一性百分比. 视差窗口范围内最低代价是次低代价的 (1 + uniquenessRatio / 100) 倍时,最低代价对应的视差值才是该像素点的视差, 否则该像素点的视差为 0 |
| 9 | speckleRange | 散斑窗口内允许的最大波动值 |
| 10 | speckleWindowSize | 散斑滤波窗口大小,<=0时不进行散斑滤波 |
| 11 | disp12MaxDiff | 左右视差图的最大容许差异,超标清零,左右一致性检查的目的是找到遮挡点,OpenCV默认的方法直接去除掉了遮挡点的视差,小于0时跳过 |
| 12 | dispType | 视差图数据类型 |
上表是OpenCV-BM的超参数,可以看到OpenCV实现的BM算法有很多地方还是很暴力的,它的前处理和后处理都很简单,再后来的很多论文中着墨甚多的后处理步骤例如遮挡点和miss点的处理在OpenCV中都极其简陋.然而OpenCV的源码水平非常高,对于内存的使用和优化,变量类型的使用等问题绝不含糊,非常值得学习.有人对源码进行了注释[26].
预处理:X方向的sobel边缘检测和归一化
视差计算:SAD带价函数
后处理:左右视差一致性检查,散斑滤波
- OpenCV-SGBM
也称为SGM、半全局匹配算法等[9]。
观察OpenCV-BM的实现可知,在计算某一点的视差(代价)时,只考虑一个窗口内的像素,窗口外面的图像还有很多像素,但是并不会参与到本点的视差计算当中.事实上有一些视差算法会考虑所有像素的影响,这种算法就叫全局算法,BM是局部算法,而SGM是半全局的.需要注意的是,OpenCV-SGBM(以下简称SGBM)对于原有的SGM(以下简称SGM)做出了一些调整.
首先看SGM算法.SGM使用分层互信息代价函数,基于动态规划的代价聚合,与OpenCV-BM类似的前处理和后处理.互信息的计算如下:
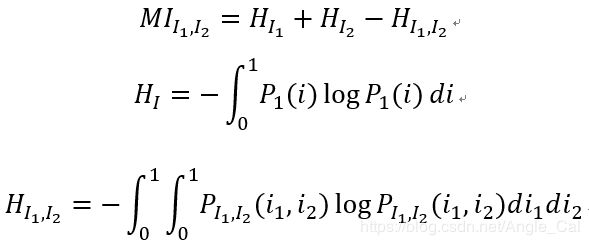
其中, M I I 1 , I 2 MI_{I_1,I_2} MII1,I2是互信息(Mutual Information), H I H_I HI是图 I I I的熵, P i P_i Pi代表某个点 i i i的概率分布,也就是灰度直方图为 i i i的点出现的概率;对应地, P I 1 , I 2 P_{I_1,I_2} PI1,I2就是两个图对应点 i 1 i_1 i1和 i 2 i_2 i2的联合概率分布,也就是:
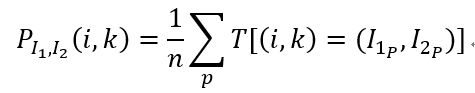
Kim等人[27]将 H I 1 , I 2 H_{I_1,I_2} HI1,I2的计算方法做了一个改进,利用泰勒展开转化为求和问题:
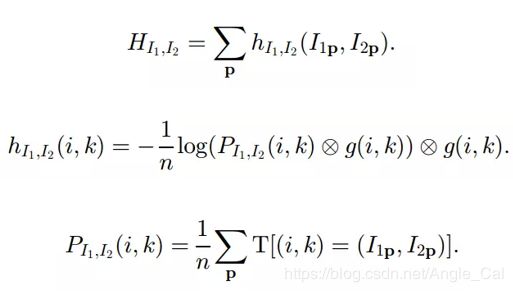
其中⨂表示卷积运算, g ( i , k ) g(i,k) g(i,k)为高斯卷积核。相应地,边缘熵以及边缘概率的计算如下:
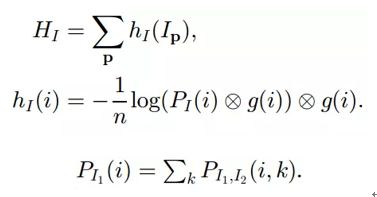
这样,互信息的定义更改为:
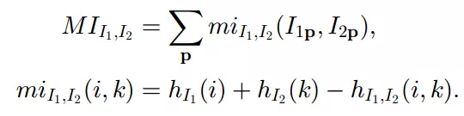
代价函数 C M I C_{MI} CMI定义为:
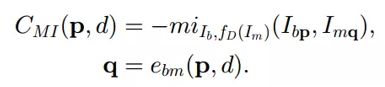
其中 q q q是点 p p p在视差为 d d d的情况下的对应校正点。原作者使用分层互信息 ( H M I ) (HMI) (HMI)进行计算,每一层尺寸减少一半。单次计算的时间复杂度是 O ( W H D ) O(WHD) O(WHD),即 w i d t h × h e i g h t × D i s p a r i t y R a n g e width×height×DisparityRange width×height×DisparityRange,所以上次迭代将会是当前迭代速度的 1 8 \frac{1}{8} 81。
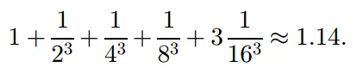
这里 1 1 6 3 \frac{1}{16^{3}} 1631 要乘3的原因是小尺寸的随机视差图不靠谱,需要迭代3次。我们可以看到,相比于后文的BT方法仅仅慢了14%.
以上是使用互信息熵代价函数的SGM,下面介绍SGBM中使用的BT方法,该方法由Birchfield和Tomasi[28]提供.
对于一个匹配序列 M M M,其代价函数 γ ( M ) γ(M) γ(M)表示匹配结果不准确的程度,其值越小越好。
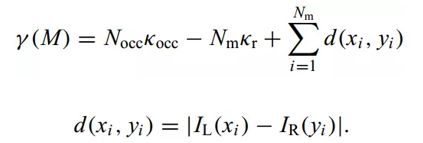
其中, k o c c k_{occ} kocc表示未匹配的惩罚项(constant occlusion penalty), k r k_r kr表示匹配的奖励项, N o c c N_{occ} Nocc和 N r N_r Nr分别表示未匹配和匹配的点数。
代价聚合:使用动态规划计算[30].设置能量函数E(D):
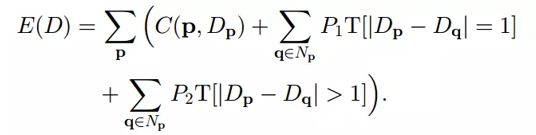
其中P1和P2分别表示视差差值为1和视差差值大于1的惩罚系数,一般P1
代价聚合公式:
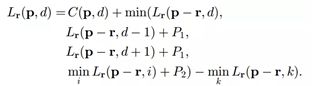
图片的代价聚合是各个像素点代价聚合之和:
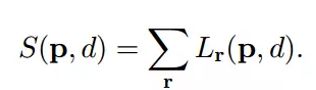
选取使代价聚合最小的视差值 m i n d S [ e m b ( q , d ) , d ] min_dS[e_{mb}(q,d),d] mindS[emb(q,d),d]即可.
OpenCV-SGBM的参数如下:
| 参数 | 参数含义 | |
|---|---|---|
| 1 | minDisparity | 最小视差值 |
| 2 | numDisparities | 视差范围 |
| 3 | blockSize | 匹配块大小,奇数,一般在[3,11] |
| 4 | P1 | P1是相邻像素视差变化±1的惩罚项 |
| 5 | P2 | P2是视差变化超过1的惩罚项,P2要大于P1 |
| 6 | disp12MaxDiff | 左右一致性检查的最大容差,小于等于0禁用检查 |
| 7 | preFilterCap | 首先计算每个像素的x导数,并将其截断到 [-preFilterCap,preFilterCap],再将结果值传递给BT代价函数 |
| 8 | uniquenessRatio | 最小代价为次小代价的百分比,常取值为[5,15] |
| 9 | speckleWindowSize | 散斑滤波窗口大小,0禁用,取值[50,200] |
| 10 | speckleRange | 连通区域的最大容差,内部乘16起效,整数,常[1,2] |
| 11 | mode | MODE_SGBM_3WAY:据我观察是微软贡献的一种HAL硬件抽象层加速的SGBM计算方法[29],其他的几种模式都调用默认的计算函数computeDisparitySGBM,包括MODE_SGBM 和MODE_HH |
-
其他算法:OpenCV-GC,LibElas,ADCensus
GC首发于2012年的ICPR[10].OpenCV-GC算法在3.0以后已经彻底移除,此外,在OpenCV2.4.13中曾经有过一个OpenCV-VAR算法,后来也移除了,在3.4.11中又出现了binnary_bm和binnary_sgbm算法,由于3.4.11是3的最后一个版本,在4之后,这两个算法也移除了,在此不过多介绍.
然而不得不说的是,曾经出现的GC算法效果还是很不错的,能够生成非常接近Groundtruth的边缘锐利且平直的视差图,Var算法生成的的视差图很稀疏,不过其中的物体轮廓非常明显,效果类似于canny算子,这两个方法速度很慢且无法进行并行化.
LibElas效果很不错,由于提供了编写良好的代码[12],应用极其广泛.首发于2011年ACCV[13].LibElas使用了自适应视差范围和基于稳健匹配点的先验知识,且易于并行化,作者给出的实现的确很快,然而效果却不尽如人意.我的观察是作者为了比赛效果使用了很多的后处理,似乎有一些填充过程造成了相反的效果.
首发于2011年ICCV[11],第三方代码[21]实现效率奇差.创新点是使用了组合的代价函数和cross-based代价聚合,代价函数本身并没有什么亮点,但是一个简单的归一化和权重处理却能优势互补;cross-based代价聚合非常利于GPU实现,整个方法基本没有什么复杂的计算,就效果来看ADCensus的效果非常好,而且参数的适应性很强. -
基于深度学习的视差算法
一些代表性成果:[14], AdaptWeight[15],次年稍加改动[16],深度学习[17],光流法[18], DERS[19],DERS in pndn[22].此外,在KITTI等比赛上,视差算法的竞争依然在进行着,目前比较多的工作集中在单目视差或深度预测上.
根据
测量,三维重建
此处我们仅在双目视觉的框架下讨论测量和三维重建的问题.
测量指的是通过双目系统获知图像上一点到相机的距离或者图像上两点之间的距离,三维重建指的获取三维点云.实际上,当我们有了精确的视差值之后,这两个问题就变的容易了.
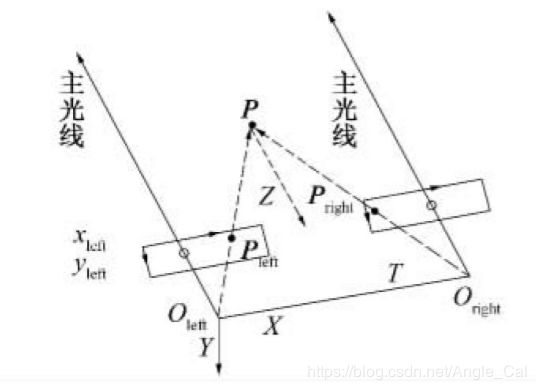
经过校正后的双目相机模型如上图,其中 P l e f t P_{left} Pleft的坐标是 ( x l , y l ) (x_l,y_l) (xl,yl), P r i g h t P_{right} Pright的坐标是 ( x r , y r ) (x_r,y_r) (xr,yr),视差定义为 d = x l − x r d=x_l-x_r d=xl−xr, f f f是焦距, T T T是基线长度,则有:
T Z = T − d Z − f \frac{T} {Z}=\frac{T-d}{Z-f} ZT=Z−fT−d,即 Z = f T d Z=\frac{fT}{d} Z=dfT
示例程序
双目视觉程序: https://github.com/jiafeng5513/Evision
新版程序演示视频:https://www.bilibili.com/video/av46024738
旧版程序演示视频:https://www.bilibili.com/video/av8862669
参考文献
- KANADE T, KANO H, KIMURA S, et al. Development of a video-rate stereo machine: Ieee/rsj International Conference on Intelligent Robots and Systems 95. ‘human Robot Interaction and Cooperative Robots’, Proceedings, 2002[C].
- KIM J, KOLMOGOROV V, ZABIH R. Visual Correspondence Using Energy Minimization and Mutual Information: IEEE International Conference on Computer Vision, 2003. Proceedings, 2008[C].
- EGNAL G. Mutual Information as a Stereo Correspondence Measure[J]. Technical Reports, 2000.
- MA L, LI J, MA J, et al. A Modified Census Transform Based on the Neighborhood Information for Stereo Matching Algorithm: Seventh International Conference on Image and Graphics, 2013[C].
- BAIK Y K, JO J H, LEE K M. Fast Census Transform-based Stereo Algorithm using SSE2: The 12th Korea-Japan Joint Workshop on Frontiers of Computer Vision, Tokushima, Japan, 2006[C].
- GU Z, SU X, LIU Y, et al. Local stereo matching with adaptive support-weight, rank transform and disparity calibration[J]. Pattern Recognition Letters, 2008,29(9):1230-1235.
- BANKS J, BENNAMOUN M, KUBIK K, et al. A constraint to improve the reliability of stereo matching using the rank transform: Acoustics, Speech, and Signal Processing, 1999. on 1999 IEEE International Conference, 1999[C].
- BIRCHFIELD S, TOMASI C. A Pixel Dissimilarity Measure That Is Insensitive to Image Sampling[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 1998,20(4):401-406.
- Stereo Processing by Semiglobal Matching and Mutual Information
- Realistic CG Stereo Image Dataset with Ground Truth Disparity Maps
- On Building an Accurate Stereo Matching System on Graphics Hardware
- http://www.cvlibs.net/software/libelas/
- Efficient Large-Scale Stereo Matching
- Cross-Scale Cost Aggregation for Stereo Matching, https://github.com/rookiepig/CrossScaleStereo#GF
- Locally Adaptive Support-Weight Approach for Visual Correspondence Search
- Adaptive Support-Weight Approach for Correspondence Search
- Improved Stereo Matching With Constant Highway Networksand Reflective Confidence Learning
- Secrets of optical flow estimation and their principles
- http://www.fujii.nuee.nagoya-u.ac.jp/multiview-data/mpeg/DE.htm
- Stereo Matching by Training a Convolutional Neural Network to Compare Image Patches
- https://github.com/DLuensch/StereoVision-ADCensus
- http://www.pudn.com/downloads532/sourcecode/graph/texture_mapping/detail2201211.html
- http://vision.middlebury.edu/flow/data/
- http://www.cvlibs.net/datasets/kitti/eval_object.php
- https://yuiwong.org/2017/12/29/ocvbm/
- https://zhuanlan.zhihu.com/p/50801189
- Visual Correspondence Using Energy Minimization and Mutual Information
- Stan Birchfield and Carlo Tomasi. A pixel dissimilarity measure that is insensitive to image sampling. Pattern Analysis and Machine Intelligence, IEEE Transactions on, 20(4):401–406, 1998.
- https://github.com/Microsoft/opencv/commit/aea4157340b3136e67c02a5565b152dbe5c73f2e
- https://blog.csdn.net/vampireshj/article/details/53813773
- 邹宇华StereoVision:https://blog.csdn.net/chenyusiyuan/article/details/8131496