Kalman Filter 学习笔记
Kalman Filter 学习笔记
Email: [email protected]
本文目的:结合代码和理论知识,较为清楚理解基础卡尔曼滤波的原理。文章如有侵权,请联系邮箱!
卡尔曼滤波是一种高效率的递归滤波器(自回归滤波器),它能够从一系列的不完全及包含噪声的测量中,估计动态系统的状态。卡尔曼滤波的一个典型实例是从一组有限的,包含噪声的,对物体位置的观察序列(可能有偏差)预测出物体的位置的坐标及速度。
1 基础知识回顾
1.1 正太分布
f(x∣μ, σ2)=12πσ2√e−(x−μ)22σ2 f ( x ∣ μ , σ 2 ) = 1 2 π σ 2 e − ( x − μ ) 2 2 σ 2
其中, μ μ 是分布的均值或期望; σ σ 是标准差; σ2 σ 2 是方差。
正太分布的性质:
经过线性变换高斯分布仍然为高斯分布
X∼N(μ,σ)Y=AX+B}⇒Y∼N(Aμ+B,AσAT) X ∼ N ( μ , σ ) Y = A X + B } ⇒ Y ∼ N ( A μ + B , A σ A T )高斯变量线性组合仍为高斯分布
X1∼N(μ1,σ21)X2∼N(μ2,σ22)}⇒p(X1+X2)∼N(μ1+μ2,σ21+σ22+2ρσ1σ2) X 1 ∼ N ( μ 1 , σ 1 2 ) X 2 ∼ N ( μ 2 , σ 2 2 ) } ⇒ p ( X 1 + X 2 ) ∼ N ( μ 1 + μ 2 , σ 1 2 + σ 2 2 + 2 ρ σ 1 σ 2 )两个相互独立的高斯变量的乘积,仍然为高斯分布
1.2 协方差
在概率论和统计学中,协方差是两个随机变量的联合变异性的量度。如果一个变量的较大值主要与另一个变量的较大值相对应,并且对于较小值也是如此,即变量倾向于显示相似的行为,则协方差是正的。在相反情况下,当一个变量的值越大,主要对应的更小的变量值,变量往往显示相反的行为,则协方差是负的。因此,协方差的符号显示了线性关系的趋势之间的变量。协方差的大小不容易解释,因为它不是标准化的,因此取决于变量的大小。
Covariance ( 协方差 ): 具有有限二阶矩的两个联合分布的 实值随机变量 X和Y之间的协方差被定义为它们与各个预期值的偏差的预期乘积 .
Formula: cov(X,Y)=E[(X−E[X])(Y−E(Y))] c o v ( X , Y ) = E [ ( X − E [ X ] ) ( Y − E ( Y ) ) ] , E[X] E [ X ] 为 X X 的期望值。协方差有时也表示为 σXY σ X Y 或者 σ(X,Y) σ ( X , Y ) 。
Simplify formula: cov(X,Y)=E[XY]−E[X]E[Y] c o v ( X , Y ) = E [ X Y ] − E [ X ] E [ Y ] 。
性质
- cov(X,a)=0 c o v ( X , a ) = 0
- cov(X,X)=var(X) c o v ( X , X ) = v a r ( X )
- cov(X,Y)=cov(Y,X) c o v ( X , Y ) = c o v ( Y , X )
- cov(aX,bY)=ab cov(X,Y) c o v ( a X , b Y ) = a b c o v ( X , Y )
- cov(X+a,Y+b)=cov(X,Y) c o v ( X + a , Y + b ) = c o v ( X , Y )
- cov(aX+bY,cW+dV)=ac cov(X,W)+ad cov(X,V)+bc cov(Y,W)+bd cov(Y,V) c o v ( a X + b Y , c W + d V ) = a c c o v ( X , W ) + a d c o v ( X , V ) + b c c o v ( Y , W ) + b d c o v ( Y , V )
- cov(AX, BX)=A cov(X, X) BT c o v ( A X , B X ) = A c o v ( X , X ) B T
意义
单个随机变量的方差表示它分布的分散程度,两个随机变量的协方差就可以理解成它们一致的分散程度有多大
1.3 状态向量
状态向量:是一组数据,用于准确描述对象在空间中的位置以及对象的移动方式。从状态向量和足够的数学条件,可以确定对象的过去和未来位置 。
2 Kalman Filter 简述
先看 Kalman Filter 5个标准公式:
时间更新方程
X(k∣k−1)=FkX(k−1∣k−1)+BkU(k) X ( k ∣ k − 1 ) = F k X ( k − 1 ∣ k − 1 ) + B k U ( k )
P(k∣k−1)=FkP(k−1∣k−1)FTk+Qk P ( k ∣ k − 1 ) = F k P ( k − 1 ∣ k − 1 ) F k T + Q k状态更新方程
K(k)=P(k∣k−1)HTk(HkP(k∣k−1)HTk+Rk)−1 K ( k ) = P ( k ∣ k − 1 ) H k T ( H k P ( k ∣ k − 1 ) H k T + R k ) − 1
X(k∣k)=X(k∣k−1)+K(k)(Z(k)−HkX(k∣k−1)) X ( k ∣ k ) = X ( k ∣ k − 1 ) + K ( k ) ( Z ( k ) − H k X ( k ∣ k − 1 ) )
P(k∣k)=(1−K(k)Hk)P(k∣k−1) P ( k ∣ k ) = ( 1 − K ( k ) H k ) P ( k ∣ k − 1 )参数说明
Parameter Table
Name Interpretation X(k∣k−1) X ( k ∣ k − 1 ) 前一时刻预测当前时刻的状态 X(k−1∣k−1) X ( k − 1 ∣ k − 1 ) 前一时刻校正后的状态(最佳估计) Fk F k 预测矩阵 Bk B k 控制矩阵 U(k) U ( k ) 控制向量(可理解为外部输入) Qk Q k 预测过程中噪声带来的协方差矩阵 P(k∣k−1) P ( k ∣ k − 1 ) 预测值和真实值之间误差的协方差矩阵 K(k) K ( k ) 卡尔曼增益洗漱矩阵 H(k) H ( k ) 传感器数据矩阵( 状态变量到测量的转换矩阵 ) R(k) R ( k ) 传感器噪声协方差 Z(k) Z ( k ) 传感器数据的期望矩阵
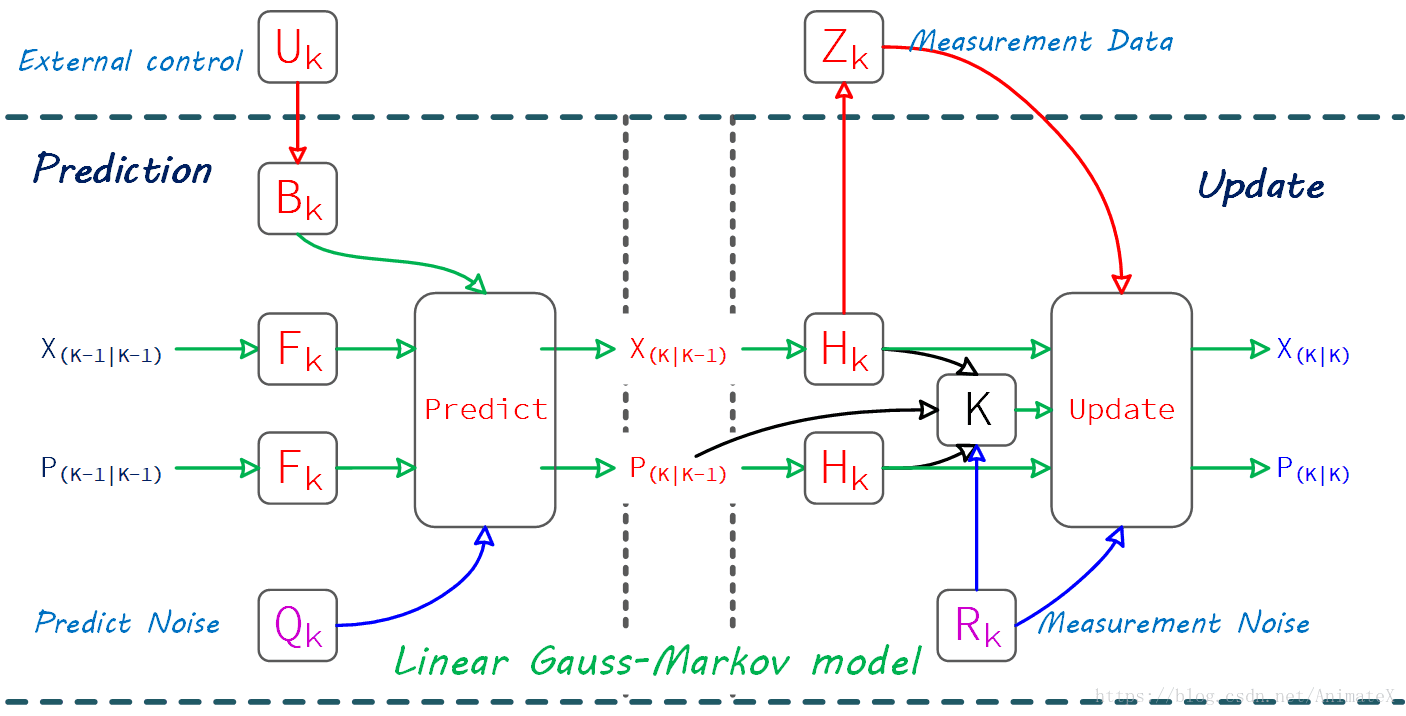
2.1 Kalman Filter 框架图
首先,注意 Kalman Filter 的模型前提:
- 系统的状态方程是线性的;
- 观测方程是线性的;
- 过程噪声符合零均值高斯分布;
- 观测噪声符合零均值高斯分布;
根据前面的公式结合隐马尔科夫链 (参考数学之美 第五章 隐含马尔可夫模型)的知识,我们可以作出对应的框图,如下图所示:
基本动态系统可以用一个马尔可夫链表示,该马尔可夫链建立在一个被高斯噪声干扰的线性算子上的。系统的状态可以用一个元素为实数的向量表示。 随着离散时间的每一次增加,这个线性算子就会作用在当前状态上,产生一个新的状态,并也会带入一些噪声,同时系统的一些已知的控制器的控制信息也会被加入。同时,另一个受噪声干扰的线性算子产生出这些隐含状态的可见输出。
其中,我们只能看见对系统施加的作用力(对于跟踪小车而言,如:加速,刹车等)的数据 Uk U k ,以及传感器回传的数据(这里需要注意:实际拿到的数据是传感器采集数据的均值(期望)) Zk Z k 。
上述框架的流程就是:通过前一时刻状态 X(k−1|k−1) X ( k − 1 | k − 1 ) 结合外在因素 Uk U k 预测出当前时刻状态 X(k|k−1) X ( k | k − 1 ) 。 再通过传感器的数据 Zk Z k 等校正当前时刻状态 X(k|k−1) X ( k | k − 1 ) 为 X(k|k) X ( k | k ) 。如此往复循环该过程。
2.2 对5个基本公式深入理解
这一节不对公式做详细的推导,仅仅进行功能上的理解。下面参考上述文章对基本的5个公式进行简单说明:
公式 1 :通过前一时刻的最佳估计值状态和外部施加的控制来预测当前时刻状态值
X(k∣k−1)=FkX(k−1∣k−1)+BkU(k) X ( k ∣ k − 1 ) = F k X ( k − 1 ∣ k − 1 ) + B k U ( k )公式 2 :结合测量噪声方差,计算预测值和真实值之间误差的协方差矩阵
P(k∣k−1)=FkP(k−1∣k−1)FTk+Qk P ( k ∣ k − 1 ) = F k P ( k − 1 ∣ k − 1 ) F k T + Q k公式 3 :结合公式2 和 Hk H k (状态变量到测量的转换矩阵),计算卡尔曼增益
K(k)=P(k∣k−1)HTk(HkP(k∣k−1)HTk+Rk)−1 K ( k ) = P ( k ∣ k − 1 ) H k T ( H k P ( k ∣ k − 1 ) H k T + R k ) − 1公式 4 :结合卡尔曼增益和传感器数据以及 Hk H k 计算更新后的状态(即校正后的状态)
X(k∣k)=X(k∣k−1)+K(k)(Z(k)−HkX(k∣k−1)) X ( k ∣ k ) = X ( k ∣ k − 1 ) + K ( k ) ( Z ( k ) − H k X ( k ∣ k − 1 ) )公式 5 :更新预测误差协方差矩阵
P(k∣k)=(1−K(k)Hk)P(k∣k−1) P ( k ∣ k ) = ( 1 − K ( k ) H k ) P ( k ∣ k − 1 )
已知一个线性系统的状态方程为:
Xk=FXK−1+BUk−1+wk−1 X k = F X K − 1 + B U k − 1 + w k − 1其中, X X 是系统的状态变量,其中,前一个状态是 X(k−1∣k−1) X ( k − 1 ∣ k − 1 ) , F F 为转换矩阵, Uk−1 U k − 1 为系统输入, B B 是将输入转换为状态变量的矩阵 ,随机变量 wk−1 w k − 1 为该线性系统的高斯噪声。注意各个矩阵的大小。这里用代码表示,如下:
% x, F, B, U, w 的矩阵大小说明
% [row, col] = size(Matrix);
% [n, 1] = size(x);
% [n, n] = size(F);
% [n, k] = size(B);
% [k, 1] = size(U);这里用一个小车运动(匀加速),简单描述5个标准公式怎么得来。假设小车收到的外力为 f f ,这里用 S S 和 v v 分别表示小车运动的路程和速度。则有:
进一步化简:
即:
这里我们得到了对应的预测方程(需要注意这里的矩阵大小)。由前面可将该过程看作高斯噪声+线性马尔可夫模型,那仅靠预测方程无法实现正确的预测。那加一个(负)反馈吧,如果预测错了就通过反馈进行校正。实际上则是通过各种传感器等回传给我们数据(服从高斯分布)进行校正。
由于传感器反馈的数据不同于我们跟踪的 ‘状态’ 的单位和尺度。我们需要转换矩阵 Hk H k 来表示传感器反馈的数据。
其中, zk z k 是测量值,大小是 m×1 m × 1 , Hk H k 大小是 m×n m × n , vk v k 是测量噪声。
对于状态方程中的系统噪声 w w 和测量噪声 v v ,假设服从如下多元高斯分布,并且 w,v w , v 是相互独立的。则:
其中, Q,R Q , R 为噪声变量的协方差矩阵。
结合前面的预测和后面的测量,我们是不是能得出实际小车的位置。则能通过当前时刻预测的的状态 x(k∣k−1) x ( k ∣ k − 1 ) 结合当前时刻的测量 z(k∣k) z ( k ∣ k ) 得到真正小车位置和速度的估计值: x(k∣k) x ( k ∣ k )
其中, z(k∣k−1) z ( k ∣ k − 1 ) 为测量值 zk z k 的预测,则 zk−Hx(k∣k−1) z k − H x ( k ∣ k − 1 ) 越小则预测值和实际测量值越接近,即预测越准确。 zk−Hx(k∣k−1) z k − H x ( k ∣ k − 1 ) 即为测量残差。上述公式中出现的 Kk K k 如何计算?
先看误差协方差矩阵:
对于小车运动的模型,我们可以得到:
对其进行简化:
即:
上式对K求导,
更完整更直观的描述参考这篇文章 :How a Kalman filter works 。
3 Kalman Filter 验证学习
3.1 房间温度预测示例
Kalman filter 用在一维温度数据测量系统中
function main
num_iter = 100; % Continus mesaure 100 time.
sz = [num_iter, 1]; % Create 'vector = [100, 1]'
x = 26; % The True tempture is 26
Q = 4e-4; % Variance of temperature Predicition
R = 0.25; % Measuring Variance, measurement accuracy of reaction Thermometer
T_start = 25; % Initial Temperature (Value) Estimate
delta_start = 1; % Initial Estimated Variance of temperature
% The temperature initial z is the measurement result of the thermometer,
% and a Gaussian noise with a variance of 0.25 is added to the true value.
z = x + sqrt(R) * randn(sz);
state_kalman = zeros(sz); % Initial array
% An estimate of the temperature. That is, at time k,
% combined with the current measured value of the thermometer and the predicted value at time k-1,
% the final estimated value is obtained.
variance_kalman = zeros(sz); % Estimate of Variance
state_pre = zeros(sz); % Prediction of temperature
variance_pre = zeros(sz); % Variance of predicted values
K = zeros(sz); % Kalman Gain
state_kalman(1) = T_start; % Temperature Estimate initialization
variance_kalman(1) = delta_start; % Estimation value Variance initialization
%% Part 2
% loop Test
for k = 2 : num_iter
% Use the best estimate of the previous moment
% as the prediction of the temperature at the current moment
state_pre(k) = state_kalman(k - 1);
% The predicted variance is the sum of the variance of the temperature optimal estimate
% and the Gaussian noise variance at the previous moment.
variance_pre(k) = variance_kalman(k - 1) + Q;
% Compute Kalman Gain
K(k) = variance_pre(k) / ( variance_pre(k) + R );
% Combined with the measured value of the current time thermometer,
% the prediction of the previous moment is corrected to obtain the corrected optimal estimate.
% Since it is a direct measurement, C is 1.
state_kalman(k) = state_pre(k) + K(k) * (z(k) - state_pre(k));
% Calculate the variance of the final estimate for the next iteration
variance_kalman(k) = (1 - K(k)) * variance_pre(k);
end
%% Part 3
% Plot Figure
FontSize = 14;
LineWidth = 3;
figure( ), plot( z, 'k+' ); % Plot temperature measure Value.
hold on;
plot( state_kalman, 'b-', 'LineWidth', LineWidth ) % Plot the best estimate Value
hold on;
plot( x * ones(sz), 'g-', 'LineWidth', LineWidth ); % Plot the True Temperqture Value
legend( 'Measure Value', 'Kalman Estimate', 'True Value');
xl=xlabel( 'Time(min)' );
yl=ylabel( 'Tempture' );
set( xl, 'fontsize', FontSize );
set( yl, 'fontsize', FontSize );
hold off;
set( gca, 'FontSize', FontSize );
figure( );
valid_iter = 2 : num_iter; % variance_pre not valid at step 1
% Plot the variance of the optimal estimate
plot( valid_iter, variance_kalman( valid_iter ), 'LineWidth', LineWidth );
legend( 'Kalman Estimate error estimate' );
xl=xlabel( 'Time(min)' );
yl=ylabel( 'C^2' );
set( xl, 'fontsize', FontSize );
set( yl, 'fontsize', FontSize );
set( gca,'FontSize', FontSize );3.2 根据GPS预测船的位置
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% Kalman滤波在船舶GPS导航定位系统中的应用
% 原作: 黄小平
% Revised: AnimateX
% Date: 2018-08-20
% Note: 船在水面(斜线运动);
% 初始位置(-100m, 200m);
% x方向(水平)运动速度v_x为: 2m/s
% y方向(垂直)运动速度v_y为: 20m/s
% GPS接收机的扫描周期T: 1s
% 观测噪声的均值为0,方差为100
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function main
clc; clear;
%% Part 1: Para Initialization
T = 1; % 雷达扫描周期
N = 80 / T; % 总的采样次数
X = zeros(4, N); % 目标的真实位置和速度, X = [S_x, v_x, S_y, v_y]^T
X(:, 1) = [-100, 2, 200, 20]; % 初始化船的位置和速度
Z = zeros(2, N); % 传感器对位置的预测
Z(:, 1) = [X(1, 1), X(3, 1)]; % 观测值初始化
delta_w = 1e-2; % 过程噪声相关参数,如果增大,曲线会明显变化。
Q = delta_w * diag([0.5, 1, 0.5, 1]); % 过程(预测状态过程)噪声方差
R = 100 * eye(2); % 观测噪声方差
F = [1, T, 0, 0; 0, 1, 0, 0; 0, 0, 1, T; 0, 0, 0, 1]; % 预测矩阵 F
H = [1, 0, 0, 0; 0, 0, 1, 0]; % 观测矩阵 H
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%% Part 2: Kalman Filter
for t = 2 : N
X(:, t) = F * X(:, t - 1) + sqrtm(Q) * randn(4, 1); % 目标真实轨迹
Z(:, t) = H * X(:, t) + sqrtm(R) * randn(2, 1); % 对目标进行观测
end
Xkf = zeros(4, N);
Xkf(:, 1) = X(:, 1); % Kalman filter 滤波初始化
P0 = eye(4); % 协方差矩阵初始化
for i = 2 : N
Xn = F * Xkf(:, i - 1); % 预测
P1 = F * P0 * F' + Q; % 预测误差协方差
K = P1 * H' * inv(H * P1 * H' + R); % 计算kalman 增益
Xkf(:, i) = Xn + K * (Z(:, i) - H * Xn); % 状态更新
P0 = (eye(4) - K * H) * P1; % 滤波误差协方差 更新
end
for i = 1 : N
Err_Observation(i) = RMS(X(:, i), Z(:, i)); % 滤波前的误差
Err_KalmanFilter(i) = RMS(X(:, i), Xkf(:, i)); % 滤波后的误差
end
%% Part 3: Plot Result
figure
hold on; box on;
plot(X(1, :), X(3, :), '-k');
plot(Z(1, :), Z(2, :), '-b.');
plot(Xkf(1, :), Xkf(3, :), '-r+');
legend('Real track', 'Observe track', 'Kalman Filter track')
figure
hold on; box on;
plot(Err_Observation, '-ko', 'MarkerFace', 'g')
plot(Err_KalmanFilter, '-ks', 'MarkerFace', 'r')
legend('Error before filtering', 'Error after filtering')
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function dist = RMS(X1, X2);
if length(X2) <= 2
dist = sqrt( (X1(1) - X2(1))^2 + (X1(3) - X2(2))^2 );
else
dist = sqrt( (X1(1) - X2(1))^2 + (X1(3) - X2(3))^2 );
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Reference
详细推导: CSND Blog 1
图文并茂: CSDN Blog 2
Code 出自 《卡尔曼滤波原理及应用 — MATLAB仿真》