运筹优化（十二）--带约束非线性规划（NLP）

线性约束的非线性规划

许多可以被有效解决的大型非线性规划中所有或者几乎所有的约束，都是线性的。只是将目标函数扩展为非线性。相对来说容易解决。

下面四种规划是特殊的NLP问题

凸规划

若最优化问题的目标函数为凸函数，不等式约束函数也为凸函数，等式约束函数是仿射的，则称该最优化问题为凸规划。凸规划的可行域为凸集，因而凸规划的局部最优解就是它的全局最优解。当凸规划的目标函数为严格凸函数时，若存在最优解，则这个最优解一定是唯一的最优解。

设f(x)是凸函数, gi(x)是凸函数, hj(x)是线性函数. 
那么这个问题的可行域S就是m+l个凸集的交, 还是凸集.

凸规划容易处理，是因为其局部最优解就是全局最优解这个特性决定的。

可分离规划

如果函数s(x) 可以表示为下列部分之和：

s(x1,x2,...,xn) 定义为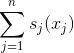：,其中每个sn(xn)都是单变量函数，则函数s(x)是可分离的，也就是说，可分离规划是指一个有约束的非线性规划满足目标函数和所有的约束函数都是可分离函数。

由于可分离规划的这种可分离性，使其容易处理，我们可以对目标函数或者约束函数，用线性函数分段近似。然后，一个可分离规划就符合凸规划的定义，可以用线性规划求解算法计算每个分段的线性规划问题，从而近似计算这个非线性规划问题。

二次规划

一类特殊的非线性规划。它的目标函数是二次函数，约束条件是线性的。求解二次规划的方法很多。较简便易行的是沃尔夫法。它是依据库恩·塔克条件，在线性规划单纯形法的基础上加以修正而成的。此外还有莱姆基法、毕尔法、凯勒法等。

正向几何规划

一类特殊的非线性规划。它的目标函数和约束函数都是正定多项式（或称正项式）。几何规划本身一般不是凸规划，但经适当变量替换，即可变为凸规划。几何规划的局部最优解必为整体最优解。求解几何规划的方法有两类。一类是通过对偶规划去求解；另一类是直接求解原规划，这类算法大多建立在根据几何不等式将多项式转化为单项式的思想上。

拉格朗日乘子法

在求取有约束条件的优化问题时，拉格朗日乘子法（Lagrange Multiplier) 和KKT条件是非常重要的两个求取方法，对于等式约束的优化问题，可以应用拉格朗日乘子法去求取最优值；如果含有不等式约束，可以应用KKT条件去求取。当然，这两个方法求得的结果只是必要条件，只有当是凸函数的情况下，才能保证是充分必要条件。KKT条件是拉格朗日乘子法的泛化。

一. 拉格朗日乘子法（Lagrange Multiplier) 和KKT条件

通常我们需要求解的最优化问题有如下几类：

(i) 无约束优化问题，可以写为:

                                      min f(x);  

(ii) 有等式约束的优化问题，可以写为:

                                       min f(x), 

                                            s.t. h_i(x) = 0; i =1, ..., n 

(iii) 有不等式约束的优化问题，可以写为：

                                      min f(x), 

                                            s.t. g_i(x) <= 0; i =1, ..., n

                                                  h_j(x) = 0; j =1, ..., m

对于第(i)类的优化问题，常常使用的方法就是Fermat定理，即使用求取f(x)的导数，然后令其为零，可以求得候选最优值，再在这些候选值中验证；如果是凸函数，可以保证是最优解。

对于第(ii)类的优化问题，常常使用的方法就是拉格朗日乘子法（Lagrange Multiplier) ，即把等式约束h_i(x)用一个系数与f(x)写为一个式子，称为拉格朗日函数，而系数称为拉格朗日乘子。通过拉格朗日函数对各个变量求导，令其为零，可以求得候选值集合，然后验证求得最优值。拉格朗日乘子法必须保证约束只含等式。

对于第(iii)类的优化问题，常常使用的方法就是KKT条件。同样地，我们把所有的等式、不等式约束与f(x)写为一个式子，也叫拉格朗日函数，系数也称拉格朗日乘子，通过一些条件，可以求出最优值的必要条件，这个条件称为KKT条件。

(a) 拉格朗日乘子法（Lagrange Multiplier)

对于等式约束，我们可以通过一个拉格朗日系数a 把等式约束和目标函数组合成为一个式子L(a, x) = f(x) + a*h(x), 这里把a和h(x)视为向量形式，a是横向量，h(x)为列向量，然后求取最优值，可以通过对L(a,x)对各个参数求导取零（拉格朗日函数的驻点），联立等式进行求取。

一开始，之所以构造拉格朗日函数，是因为它在所有的可行点上都和原始目标函数相同。对于任何固定的拉格朗日乘子v，松弛模型（就是带约束转换为无约束后的模型）的无约束最优解一定是一个驻点。如果x是拉格朗日函数L的一个驻点，而x又是L的无约束最优解，则x一定是原始带等式约束的NLP的最优解。

(b) KKT条件

对于含有不等式约束的优化问题，如何求取最优值呢？常用的方法是KKT条件，同样地，把所有的不等式约束、等式约束和目标函数全部写为一个式子L(a, b, x)= f(x) + a*g(x)+b*h(x)，KKT条件是说最优值必须满足以下条件：

1. L(a, b, x)对x求导为零；

2. h(x) =0;

3. a*g(x) = 0;

求取这三个等式之后就能得到候选最优值。其中第三个式子非常有趣，因为g(x)<=0，如果要满足这个等式，必须a=0或者g(x)=0. 这是SVM的很多重要性质的来源，如支持向量的概念。

也就是说，在局部最优点上，对于每条不等式约束，要么其作用，要么其对应的拉格朗日乘子为0

惩罚与障碍法

这部分与线性规划的内点法思想类似，将带约束问题，转换到无约束问题，通过惩罚函数的方式。

既约梯度法

既约梯度法(Reduced Gradient Method，1963)，将线性规划的单纯形法推广到具有非线性目标函数的问题.其基本思想是把变量分为基变量和非基变量，将基变量用非基变量表示，并从目标函数中消去基变量，得到以非基变量为自变量的简化的目标函数，进而利用此函数的负梯度构造下降可行方向。简化后的目标函数关于非基变量的梯度称为目标函数的既约梯度。