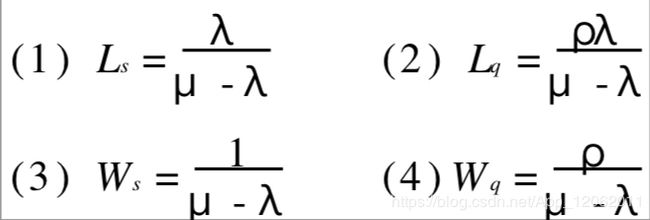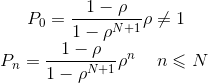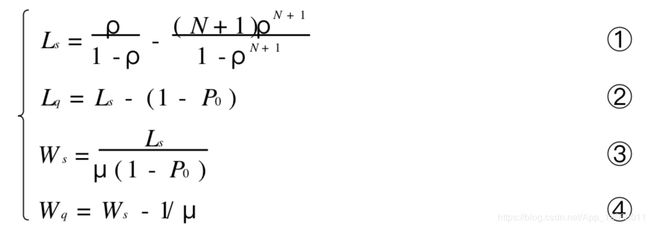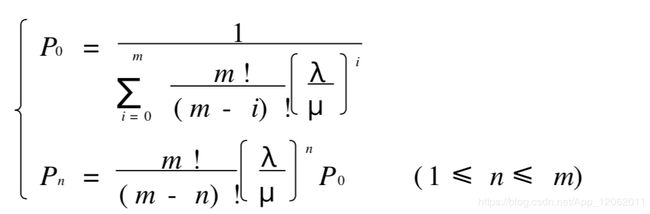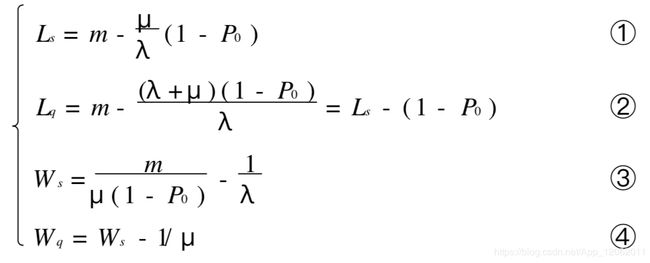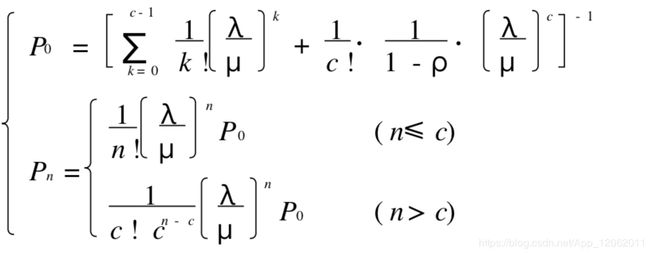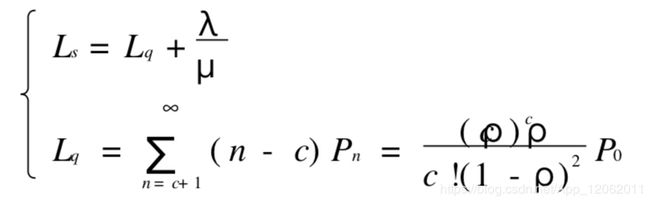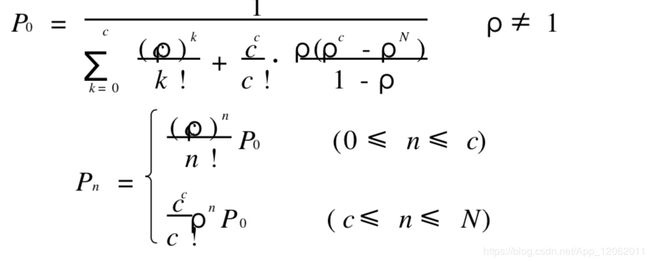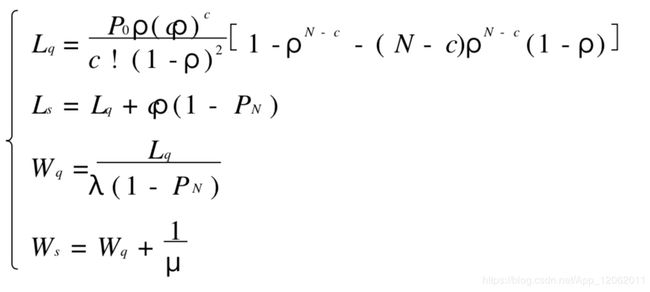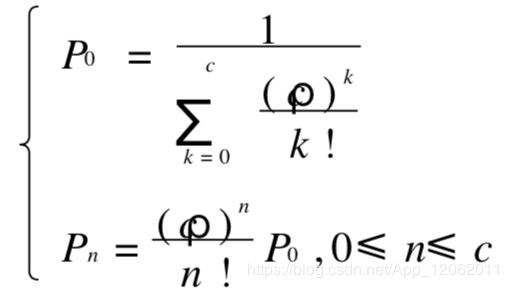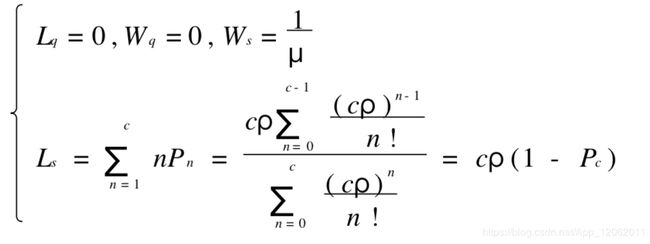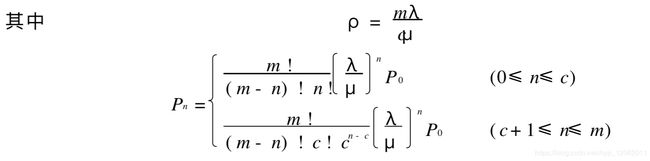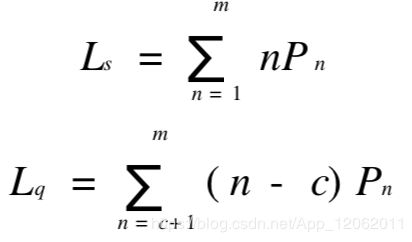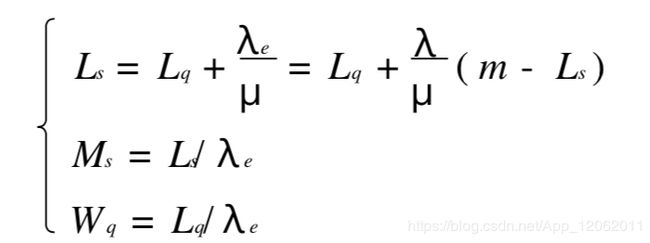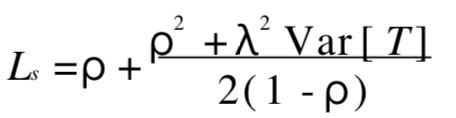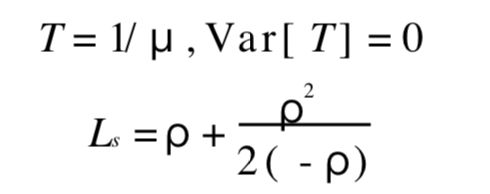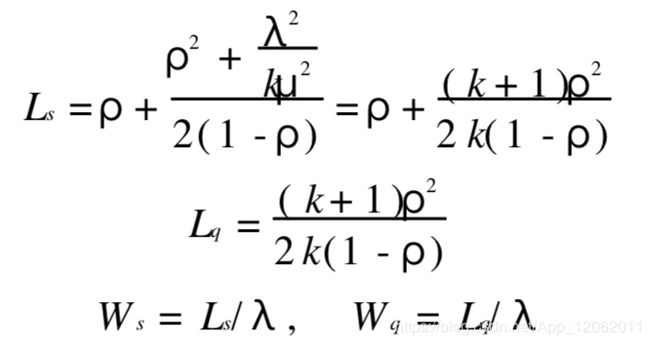运筹优化（十六）--排队论基础及其最优化求解

排队过程的一般表示

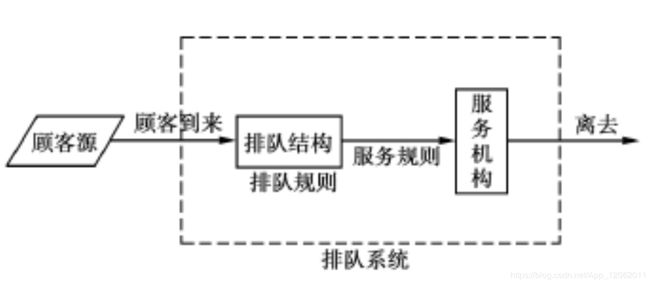
下图1就是排队过程的一般模型。各个顾客由顾客源(总体)出发,到达服务机构 (服务台、服务员)前排队等候接受服务, 服务完成后就离开。排队结构指队列的数目和排列方式 , 排队规则和服务规则是说明顾客在排队系统中按怎样的规 则、次序接受服务的。我们所说的排队系统就指图中虚线所包括的部分。

排队系统的组成和特征

一般的排队系统都有三个基本组成部分 : 1输入过程 ; 2排队规则 ; 3服务机构。

1. 输入过程

输入即指顾客到达排队系统 , 可能有下列各种不同情况 , 当然这些情况并不是彼此排斥的。

(1) 顾客的总体(称为顾客源)的组成可能是有限的,也可能是无限的。上游河水流入水库可以认为总体是无限的 , 工厂内停机待修的机器显然是有限的总体。

(2) 顾客到来的方式可能是一个一个的, 也可能是成批的。例如到餐厅就餐就有单个到来的顾客和受邀请来参加宴会的成批顾客，我们将只研究单个到来的情形。

(3) 顾客相继到达的间隔时间可以是确定型的, 也可以是随机型的。

(4) 顾客的到达可以是相互独立的,就是说,以前的到达情况对以后顾客的到来没有影响 , 否则就是有关联的 。

(5) 输入过程可以是平稳的,或称对时间是齐次的,是指描述相继到达的间隔时间分布和所含参数(如期望值、方差等)都是与时间无关的, 否则称为非平稳的。

2. 排队规则

(1) 顾客到达时, 如所有服务台都正被占用,在这种情形下顾客可以随即离去, 也可以排队等候。随即离去的称为即时制或称损失制 , 因为这将失掉许多顾客 ; 排队等候的称为等待制。普通市内电话的呼唤属于前者 , 而登记市外长途电话的呼唤属于后者。对于等待制,为顾客进行服务的次序可以采用下列各种规则: 先到先服务, 后到先服 务 , 随机服务 , 有优先权的服务等。

先到先服务 , 即按到达次序接受服务 , 这是最通常的情形。后到先服务,如乘用电梯的顾客常是后入先出的。仓库中存放的厚钢板也是如此。 在情报系统中 , 最后到达的信息往往是最有价值的 , 因而常采用后到先服务 ( 指被采用 ) 的 规则。

随机服务 , 指服务员从等待的顾客中随机地选取其一进行服务 , 而不管到达的先后 , 如电话交换台接通呼唤的电话就是如此。

有优先权的服务 , 如医院对于病情严重的患者将给予优先治疗。

(2) 从占有的空间来看,队列可以排在具体的处所(如售票处、候诊室等),也可以是抽象的 ( 如向电话交换台要求通话的呼唤 ) 。由 于空间的限制或其他原因 , 有的系统要规定容量(即允许进入排队系统的顾客数)的最大限;有的没有这种限制(即认为容量可以是无限的)。

(3) 从队列的数目看, 可以是单列, 也可以是多列。在多列的情形, 各列间的顾客有的可以互相转移,有的不能(如用绳子或栏杆隔开)。有的排队顾客因等候时间过长而中途退出 , 有的不能退出 ( 如高速公路上的汽车流 ) , 必须坚持到被服务为止。

3. 服务机构

从机构形式和工作情况来看有以下几种情况。

(1) 服务机构可以没有服务员,也可以有一个或多个服务员(服务台、通道、窗口等)。 例如 , 在敞架售书的书店 , 顾客选书时就没有服务员 , 但交款时可能有多个服务员。

(2) 在有多个服务台的情形中,它们可以是平行排列(并列)的,可以是前后排列(串 列)的, 也可以是混合的。

(3) 服务方式可以对单个顾客进行,也可以对成批顾客进行,公共汽车对在站台等候 的顾客就成批进行服务。

(4) 和输入过程一样, 服务时间也分确定型的和随机型的。自动冲洗汽车的装置对每辆汽车冲洗 ( 服务 ) 的时间就是确定型的 , 但大多数情形的服务时间是随机型的。对于随机型的服务时间 , 需要知道它的概率分布。如果输入过程 , 即相继到达的间隔时间和服务时间二者都是确定型的 , 那么问题就太 简单了。因此 , 在排队论中所讨论的是二者至少有一个是随机型的情形。

(5) 和输入过程一样, 服务时间的分布我们总假定是平稳的, 即分布的期望值、方差等参数都不受时间的影响。

排队模型的分类

D .G .Kendall 在 1953 年提出排队模型分类方法 , 影响最大的特征有三个, 即：

(1) 相继顾客到达间隔时间的分布;

(2) 服务时间的分布;

(3) 服务台的个数。

按照这三个特征分类 , 并用一定符号表示 , 称为 Kendall 记号。 这只对并列的服务台 (如果服务台是多于一个的话)的情形,他用的符号形式是:

X/ Y/ Z

其中 , X 处填写表示相继到达间隔时间的分布;

Y 处填写表示服务时间的分布;

Z 处填写并列的服务台的数目。

表示相继到达间隔时间和服务时间的各种分布的符号是:

M——负指数分布( M是 Markov的字头,因为负指数分布具有无记忆性,即 Markov性);
D——确定型(deterministic);
Ek ——k阶爱尔朗(erlang)分布;
GI—— 一般相互独立(general independent)的时间间隔的分布; G—— 一般(general)服务时间的分布。

例如, M/ M/ 1 表示相继到达间隔时间为负指数分布、服务时间为负指数分布、单服务台的模型; D/ M/ c 表示确定的到达间隔、服务时间为负指数分布、c个平行服务台(但顾客是一队)的模型。

以后 , 在 1971 年一次关于排队论符号标准化会议上决定 , 将 Kendall 符号扩充成为 : X/ Y/ Z/ A/ B/ C 形式 , 其中前三项意义不变 , 而后三项意义分别是 :

A 处填写系统容量限制N ;
B 处填写顾客源数目m;
C 处填写服务规则 , 如先到先服务( FCFS) , 后到后服务( LCFS)等。

并约定 , 如略去后三项 , 即指 X/ Y/ Z/ ∞/ ∞/ FCFS 的情形。这里只讨论先到先服务FCFS 的情形 , 所以略去第六项。

排队问题的求解

一个实际问题作为排队问题求解时 , 首先要研究它属于哪个模型 , 其中只有顾客到达的间隔时间分布和服务时间的分布需要实测的数据来确定 , 其他因素都是在问题提出时给定的。

解排队问题的目的,是研究排队系统运行的效率, 估计服务质量, 确定系统参数的最优值 , 以决定系统结构是否合理、研究设计改进措施等。所以必须确定用以判断系统运行优劣的基本数量指标 , 解排队问题就是首先求出这些数量指标的概率分布或特征数。 这 些指标通常是 :

(1) 队长,指在系统中的顾客数,它的期望值记作 Ls;

排队长(队列长),指在系统中排队等待服务的顾客数,它的期望值记作 Lq;

系统中顾客数 =  在队列中等待服务的顾客数 + 正被服务的顾客数

一般情形, Ls (或 Lq )越大,说明服务率越低,排队成龙,是顾客最厌烦的。

(2) 逗留时间,指一个顾客在系统中的停留时间,它的期望值记作 Ws;

等待时间, 指一个顾客在系统中排队等待的时间, 它的期望值记作 Wq ,

逗留时间 = 等待时间 + 服务时间

在机器故障问题中 , 无论是等待修理或正在修理都使工厂受到停工的损 失。所以逗留时间(停工时间)是主要的。但一般购物、诊病等问题中仅仅等待时间常是顾客们所关心的。

此外,还有忙期( busy period)指从顾客到达空闲服务机构起到服务机构再次为空闲止这段时间长度, 即服务机构连续繁忙的时间长度, 它关系到服务员的工作强度。忙期和一个忙期中平均完成服务顾客数都是衡量服务机构效率的指标。

在即时制或排队有限制的情形, 还有由于顾客被拒绝而使企业受到损失的损失率以及以后经常遇到的服务强度等 , 这些都是很重要的指标。

计算这些指标的基础是表达系统状态的概率。所谓系统的状态即指系统中顾客数 , 如果系统中有n个顾客就说系统的状态是 n,它的可能值是:

(1) 队长没有限制时,n=0,1,2,⋯
(2) 队长有限制,最大数为N时,n=0,1,2,⋯,N
(3) 即时制,服务台个数是 c时, n=0,1,2,⋯,c
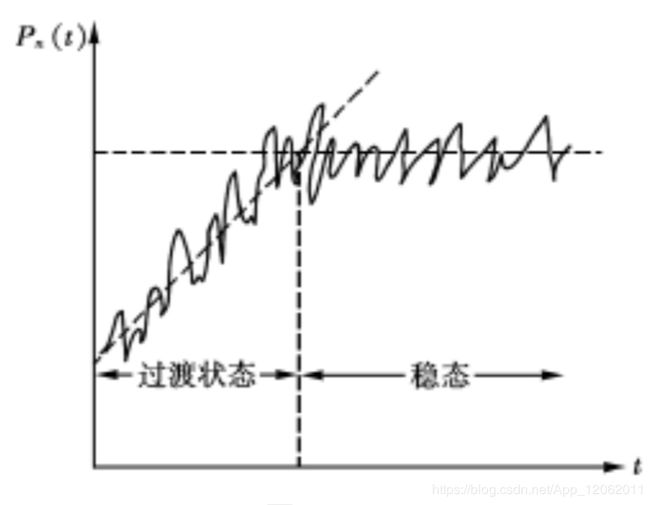
后者,状态n又表示正在工作(繁忙)的服务台数。这些状态的概率一般是随时刻t而变化, 所以在时刻t、系统状态为n的概率用Pn(t)表示。求状态概率 Pn (t)的方法,首先要建立含 Pn (t)的关系式见下图,因为t是连续变量,而n只取非负整数,所以建立的Pn(t)的关系式 一般是微分差分方程(关于t的微分方程,关于n的差分方程)。方程的解称为瞬态(或称过渡状态)(transient state)解。求瞬态解是不容易的, 一般地, 即使求出也很难利用, 因此我们常用它的极限(如果存在的话 )：

称为稳态(steady state) , 或称统计平衡状态(statistical equilibrium state)的解。

 

稳态的物理含义是, 当系统运行了无限长的时间之后 , 初始 ( t = 0 ) 出发状态的概率分布( Pn (0), n≥0)的影响将消失,而且系统的状态概率分布不再随时间变化。当然,在实际应用中大多数问题系统会很快趋于稳态, 而无需等到t→∞以后。但永远达不到稳态的情形也确实存在的。求稳态概率Pn时,并不一定求t→∞时Pn(t)的极限,而只需令导数P′n(t)=0即可。以下着重研究稳态的情形。

到达间隔的分布和服务时间的分布

解决排队问题首先要根据原始资料作出顾客到达间隔和服务时间的经验分布 , 然后按照统计学的方法(例如χ2检验法)以确定适合于哪种理论分布,并估计它的参数值。经验分布就是概率分布的半参估计或者无参估计，可以用直方图平滑，也可以用核函数平滑。常见的理论分布——泊松分布、负指数分布和 爱尔朗 (Erlang)分布。这里不再啰嗦了，下面直接说明输入过程是泊松过程，服务时间服从负指数分布，单服务台的排队系统。

单服务台负指数分布排队系统的分析

按以下三种情形讨论。

1. 标 准 的 M/ M/ 1 模 型 , 即 ( M/ M/ 1/ ∞/ ∞ ) ;
2. 系 统 的 容 量 有 限 制 , 即 ( M/ M/ 1/ N/ ∞ ) ;
3. 顾客源为有限,即(M/ M/ 1/ ∞/ m)。

标准的 M/ M/ 1模型(M/ M/ 1/ ∞/ ∞)

标准的 M/ M/ 1 模型是指适合下列条件的排队系统 :

(1) 输入过程——顾客源是无限的, 顾客单个到来, 相互独立, 一定时间的到达数服从泊松分布, 到达过程已是平稳的。

(2) 排队规则——单队,且对队长没有限制,先到先服务。

(3) 服务机构——单服务台, 各顾客的服务时间是相互独立的, 服从相同的负指数分布。

此外 , 还假定到达间隔时间和服务时间是相互独立的。

在分析标准的 M/ M/ 1 模型时, 首先要求出系统在任意时刻t的状态为n(系统中有n个顾客)的概率Pn(t) ,它决定了系统运行的特征。

因已知到达规律服从参数为λ的泊松过程, 服务时间服从参数为 μ的负指数分布 , 所以在[ t, t +Δt)时间区间内分为:

1. 有1个顾客到达的概率为 λΔt+o (Δt) ; 没有顾客到达的概率就是1-λΔt+o(Δt) 。
2. 当有顾客在接受服务时,1个顾客被服务完了(离去)的概率是μΔt+o(Δt),没有离去的概率就是1- μΔt+o(Δt) 。
3. 多于一个顾客的到达或离去的概率是 o(Δt),是可以忽略的。

略去中间计算状态概率的推导过程，计算得到系统状态为 n的概率：

上式的ρ有其实际意义。根据表达式的不同, 可以有不同的解释。当 ρ= λ/μ表达时, 它是平均到达率与平均服务率之比; 即在相同时区内顾客到达的平均数与被服务的平均数之比。若表示为 ρ= (1/μ)/(1/λ) , 它是为一个顾客的服务时间与到达间隔时间之比;称ρ为服务强度(traffic intensity) ,或称ρ为话务强度。这是因为早期排队论是爱尔朗等人在研究电话理论时用的术语,一直沿用至今，ρ= 1 - P0 ,它刻画了服务机构的繁忙程度 ; 所以又称服务机构的利用率。由此，我们得出系统的运行指标：

(1) 在系统中的平均顾客数(队长期望值)： 或者 

(2) 在队列中等待的平均顾客数(队列长期望值)

关于顾客在系统中逗留的时间W(随机变量),在 M/ M/ 1 情形下,它服从参数为μ-λ 的负指数分布1 ,即:

分布函数：

概率密度：，于是得到：

(3) 在系统中顾客逗留时间的期望值

(4) 在队列中顾客等待时间的期望值

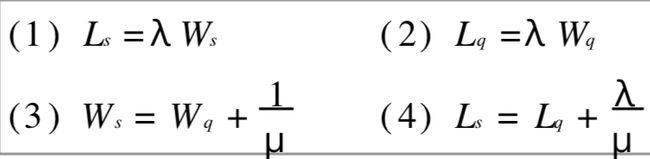
现将以上各式归纳如下 :

它们相互的关系如下 :

上式称为 Little 公式。

不同的服务规则 (先到先服务 , 后到先服务 , 随机服务 ) 它们的不同点主要反映在等待时间的分布函数的不同 , 而一些期望值是相同的。我们上面讨论的各种指标 , 因为都是期望值,所以这些指标的计算公式对三种服务规则都适用(但对有优先权的规则不适用)。

系统的容量有限制的情况( M/ M/ 1/ N/ ∞) 

如果系统的最大容量为 N,对于单服务台的情形,排队等待的顾客最多为 N - 1,在 某时刻一顾客到达时,如系统中已有 N 个顾客,那么这个顾客就被拒绝进入系统。

当 N=1时为即时制的情形;当 N→∞,为容量无限制的情形。我们仍只考虑稳态的情况（上面标准公式只考虑稳态情况）：

在对容量没有限制的情形 , 我们曾设 ρ<1, 这不仅是实际问题的需要, 也是无穷级数收敛所必需的。在容量为有限数N的情形下,这个条件就没有必要了。当ρ>1时, 表示损失率的PN(或表示被拒绝排队的顾客平均数λPN)将是很大的。

现 在 把 M/ M/ 1/ N/ ∞ 型 的 指 标 归 纳 如 下 ( 当 ρ≠ 1 时 )(计算过程略) :

顾客源为有限的情形(M/M/1/∞/m) 

 关于平均到达率 , 在无限源的情形是按全体顾客来考虑的; 在有限源的情形必须按每个顾客来考虑。为简单起见, 设各个顾客的到达率都是相同的λ, 这时在系统外的顾客平均数为m- Ls ,对系统的有效到达率λe应是λe =λ(m-Ls)

推导过程跟上面方法类似：

求得系统的各项指标为： 

多服务台负指数分布排队系统的分析 

现在讨论单队、并列的多服务台(服务台数 c)的情形,我们分以下三种情形讨论。

( 1 ) 标准的M/ M/ c 模型(M/ M/ c/ ∞/ ∞ ) ;
( 2 ) 系统容量有限制 ( M/ M/ c/ N/ ∞ ) ;
( 3 ) 有限顾客源 ( M/ M/ c/ ∞ / m ) 。

标准的M/M/c模型(M/M/c/∞/∞)

关于标准的 M/ M/ c模型各种特征的规定与标准的 M/ M/ 1 模型的规定相同。另外规定各服务台工作是相互独立(不搞协作)且平均服务率相同μ1 =μ2 =⋯=μc =μ。与标准的 M/ M/ 1推导类似：

系统的运行指标求得如下: 

平均等待时间和逗留时间仍由 Little 公式求得, 

\

系统的容量有限制的情形(M/M/c/N/∞)

设系统的容量最大限制为 N(≥c) , 当系统中顾客数n已达到N(即队列中顾客数已达N - c)时,再来的顾客即被拒绝,其他条件与标准的 M/ M/ c型相同。

系统的状态概率和运行指标如下 :

特别当 N = c(即时制)的情形, 例如在街头的停车场就不允许排队等待空位,这时:  

其中,当 n= c即关于 Pc 的公式,被称为爱尔朗呼唤损失公式,是 A. K. Erlang 早在1917年发现的, 并广泛应用于电话系统的设计中。 这时的运行指标如下:

它又是使用的服务台数(期望值) 。 

顾客源为有限的情形(M/M/c/∞/m)

设顾客总体(顾客源)为有限数m,且m>c,和单服务台情形一样,顾客到达率λ是按每个顾客来考虑的,在机器管理问题中, 就是共有m台机器, 有c个修理工人, 顾客到达就是机器出了故障, 而每个顾客的到达率λ是指每台机器每单位运转时间出故障的期望次数。系统中顾客数n就是出故障的机器台数,当n≤c时,所有的故障机器都在被修理, 有(c-n)个修理工人在空闲;当 c< n≤m时,有(n- c)台机器在停机等待修理,而修理工 人都在繁忙状态。假定这 c个工人修理技术相同,修理(服务)时间都服从参数为μ的负指数分布, 并假定故障的修复时间和正在生产的机器是否发生故障是相互独立的。

(2) 平均顾客数(即平均故障台数):

有效的到达率λe 应等于每个顾客的到达率λ乘以在系统外(即正常生产的)机器的期望数 : λe =λ(m-Ls)在机器故障问题中,它是每单位时间m台机器平均出现故障的次数。

其他指标：

由于 P0 , Pn 计算公式过于复杂 , 有专用图书列成表格可供使用。 

 一般服务时间M/G/1模型

前面我们研究了泊松输入和负指数的服务时间的模型。下面将讨论服务时间是任意分布的情形, 当然 , 对任何情形下面关系都是正确的。

E[系统中顾客数 ] = E[队列中顾客数] + E[服务机构中顾客数 ]

E[在系统中逗留时间 ] = E[排队等候时间] + E[服务时间 ]

Ls =λWs , Lq =λWq

Pollaczek-Khintchine( P-K) 公式

对于M/ G/ 1 模型 , 服务时间T的分布是一般的, (但要求期望值E[T]和方差Var[ T]都存在),其他条件和标准的 M/ M/ 1 型相同。为了达到稳态,ρ<1 这一条件还是必要的，其中ρ= λE[T] 。

在上述条件下 , 则有：

这就是 Pollaczek-Khintchine(P-K)公式。只要知道λ, E[ T]和Var[T] ,不管T是什么具体分布,就可求出 Ls。

由这公式还可注意到, 因为有方差项的存在 , 在研究各期望值( 各运行指标都是期望值)时,完全不考虑概率性质会得出错误结果,仅当 Var[ T] = 0 时,随机性的波动才不影响 Ls,所以要想改进各指标,除考虑期望值外,还可以从改变方差来考虑。

定长服务时间M/D/1模型

服务时间是确定的常数 , 例如在一条装配线上完成一件工作的时间就应是常数。 自动的汽车冲洗台, 冲洗一辆汽车的时间也是常数 , 这时：

注意 可以证明,在一般服务时间分布的Lq和Wq中以定长服务时间的为最小, 这符合我们通俗的理解——服务时间越有规律 , 等候 的时间就越短。 

爱尔朗服务时间M/Ek/1模型

如果顾客必须经过k个服务站, 在每个服务站的服务时间Ti相互独立 , 并服从相同的负指数分布，那么T=∑Ti 服从k阶爱尔朗分布.

对于 M/ Ek/ 1 模型(除服务时间外,其他条件与标准的 M/ M/ 1 型相同):

经济分析——系统的最优化 

排队系统的最优化问题

排队系统的最优化问题分为两类 : 系统设计的最优化和系统控制 优化。前者称为静态问题 , 从排队论一诞生起就成为人们研究的内容 , 目的在于使设备达到最大效益 , 或者说,在一定的质量指标下要求机构最为经济。后者称为动态问题, 是指一个给定的系统,如何运营可使某个目标函数得到最优,这是近10多年来排队论的研究重点之一。

在一般情形下 , 提高服务水平 (数量 , 质量 ) 自然会降低顾客的等待费用 (损失) , 但却常常增加了服务机构的成本, 我们最优化的目标之一是使二者费用之和为最小, 决定达到这个目标的最优的服务水平。另一个常用的目标函数是使纯收入或使利润(服务收入与 服务成本之差)为最大。

各种费用在稳态情形下, 都是按单位时间来考虑的。一般情形, 服务费用 (成本) 是可以确切计算或估计的。至于顾客的等待费用就有许多不同情况, 像机械故障问题中等待费用 ( 由于机器待修而使生产遭受的损失) 是可以确切估计的 , 但像病人就诊的等待费用(由于拖延治疗使病情恶化所受的损失 ) , 或由于队列过长而失掉潜在顾客所造成的营业损失，就只能根据统计的经验资料来估计。服务水平也可以由不同形式来表示, 主要的是平均服务率μ(代表服务机构的服务能力和经验等),其次是服务设备,如服务台的个数 c,以及由队列所占空间大小所决定的队列最大限制数N等,服务水平也可以通过服务强度ρ来表示。

我们常用的求解方法 , 对于离散变量常用边际分析法 , 对于连续变量常用经典的微分法, 对于复杂问题当然可以用非线性规划或动态规划的方法。

注意：

当排队系统的到达间隔时间和服务时间的概率分布很复杂时 , 或不能用公式给出时 , 那么就不能用解析法求解。