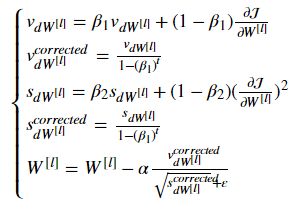吴恩达深度学习2-Week2课后作业-优化算法

一、Deeplearning-assignment

到目前为止，在之前的练习中我们一直使用梯度下降来更新参数并最小化成本函数。在本次作业中，将学习更先进的优化方法，它在加快学习速度的同时，甚至可以获得更好的最终值。一个好的优化算法可以让你几个小时内就获得一个结果，而不是等待几天。

1.Gradient Descent

在机器学习中，有一种优化方法叫梯度下降，当每次迭代使用m个样本时，它也叫批量梯度下降。

完成梯度下降的更新规则：

2.Mini-Batch Gradient descent

现在让我们学习如何从训练集(X, Y)中构建小批量数据集。

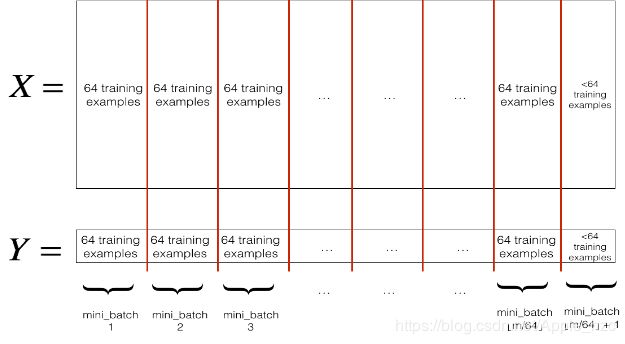
Shuffling：如下所示，将训练集(X, Y)的数据进行随机混洗. X 和 Y 的每一列代表一个训练样本. 请注意随机混洗是在X和Y之间同步完成的，这样才能保证X的第i个标签和Y的第i个标签相匹配。随机混洗是为了确保样本被随机的划分到不同的小批量集中。

Partitioning：将混洗的数据(X, Y)按固定大小(mini_batch_size这里是64)进行分区。请注意，训练样本的总数并不一定能被64整除。划分的最后一个小批量可能小于64，就像下面这样：

实现 random_mini_batches，随机混洗的代码我们已经实现了。为了进行分区，我们提供了以下代码用来索引某个特定的小批量集，比如第一个和第二个小批量集：

first_mini_batch_X = shuffled_X[:, 0 : mini_batch_size]
second_mini_batch_X = shuffled_X[:, mini_batch_size : 2 * mini_batch_size]
...

你应该记住的是：

• Shuffling and Partitioning 是构建小批量所需的两个步骤。
• mini-batch的大小通常选择的是2的幂次方, 比如 16, 32, 64, 128。

3.Momentum

由于小批量梯度下降是用整体样本的一个子集进行的参数更新，所以更新的方向会发生一定变化，小批量梯度下降会在不断摆动中趋于收敛。使用动量优化法可以减少这些振荡。

动量法会把过去的梯度变化考虑进来用来平滑更新。我们把以前梯度变化的“方向”存储在变量 vv 中。形式上，你可以把它看成前面步骤中梯度的指数加权平均值。你可以想象有一个球从上坡上滚下来，vv 就是它的“速度”，速度（和动量）的构建取决于山坡的坡度/方向。

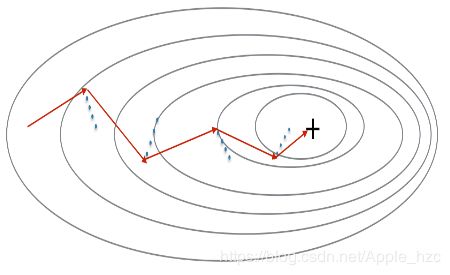
红色箭头表示采用动量优化法的小批量梯度下降每一步进行的方向. 蓝色的点表示的是每步的梯度（相对于当前小批量）方向。

momentum更新的规则是：for l = 1,...L：

β的常用值范围是从0.8到0.999。如果你不想调整它，β=0.9通常是一个合理的默认值。

4.Adam

Adam是训练神经网络最有效的优化算法之一。它结合了RMSProp（讲座中介绍）和Momentum。

Adam的更新规则是：for l = 1,...L：

5.Model with different optimization algorithms

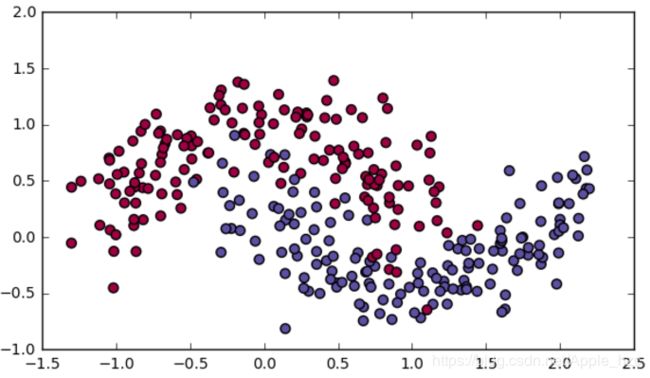
让我们使用下面的"moons"数据集来测试不同的优化方法。

现在将用3种优化方法依次运行这个3层的神经网络（详见代码中的model函数）。

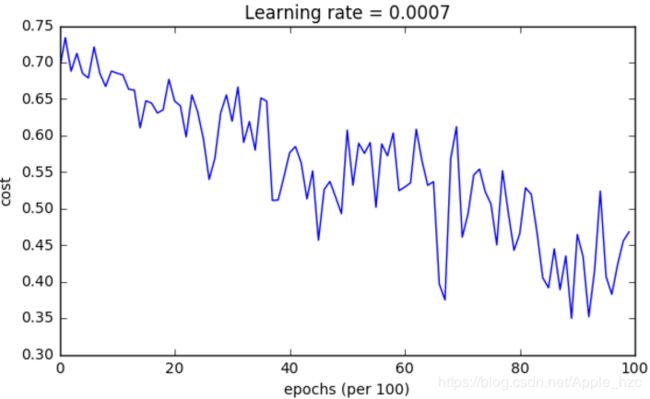
（1）Mini-batch Gradient descent

（2）Mini-batch gradient descent with momentum

由于这个例子比较简单，使用 momemtum 带来的收益较小；如果面对的是更复杂的问题，momemtum 带来的收益会更大。

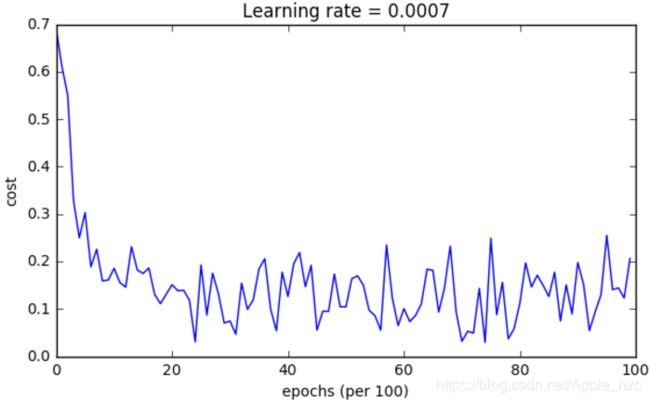
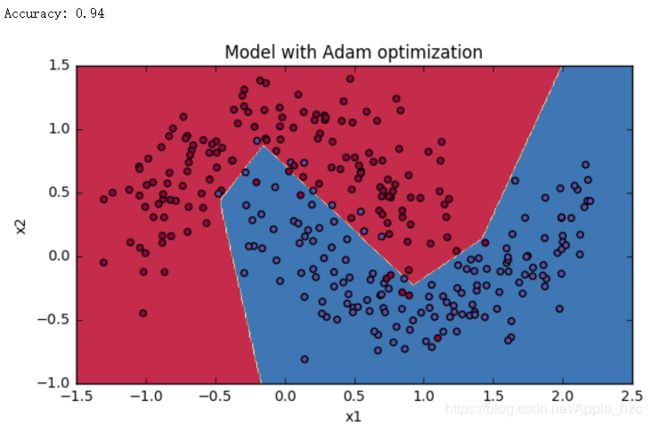
（3）Mini-batch with Adam mode

---

二、相关算法代码

import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets

from opt_utils import load_params_and_grads, initialize_parameters, forward_propagation, backward_propagation
from opt_utils import compute_cost, predict, predict_dec, plot_decision_boundary, load_dataset
from week2.testCases import *

plt.rcParams['figure.figsize'] = (7.0, 4.0)  # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'


def update_parameters_with_gd(parameters, grads, learning_rate):
    L = len(parameters) // 2
    for l in range(L):
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * grads["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * grads["db" + str(l + 1)]
        assert (parameters['W' + str(l + 1)].shape == grads["dW" + str(l + 1)].shape)
        assert (parameters['b' + str(l + 1)].shape == grads["db" + str(l + 1)].shape)

    return parameters


# parameters, grads, learning_rate = update_parameters_with_gd_test_case()
# parameters = update_parameters_with_gd(parameters, grads, learning_rate)
# print("W1 = " + str(parameters["W1"]))
# print("b1 = " + str(parameters["b1"]))
# print("W2 = " + str(parameters["W2"]))
# print("b2 = " + str(parameters["b2"]))


def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
    np.random.seed(seed)
    m = X.shape[1]
    mini_batches = []

    permutation = list(np.random.permutation(m))
    shuffled_X = X[:, permutation]
    shuffled_Y = Y[:, permutation].reshape((1, m))

    num_complete_minibatches = math.floor(m / mini_batch_size)
    for k in range(0, num_complete_minibatches):
        mini_batch_X = shuffled_X[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch_Y = shuffled_Y[:, k * mini_batch_size: (k + 1) * mini_batch_size]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    if m % mini_batch_size != 0:
        mini_batch_X = shuffled_X[:, num_complete_minibatches * mini_batch_size:]
        mini_batch_Y = shuffled_Y[:, num_complete_minibatches * mini_batch_size:]
        mini_batch = (mini_batch_X, mini_batch_Y)
        mini_batches.append(mini_batch)

    return mini_batches


# X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()
# mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
# print("shape of the 1st mini_batch_X: " + str(mini_batches[0][0].shape))
# print("shape of the 2nd mini_batch_X: " + str(mini_batches[1][0].shape))
# print("shape of the 3rd mini_batch_X: " + str(mini_batches[2][0].shape))
# print("shape of the 1st mini_batch_Y: " + str(mini_batches[0][1].shape))
# print("shape of the 2nd mini_batch_Y: " + str(mini_batches[1][1].shape))
# print("shape of the 3rd mini_batch_Y: " + str(mini_batches[2][1].shape))
# print("mini batch sanity check: " + str(mini_batches[0][0][0][0:3]))


def initialize_velocity(parameters):
    L = len(parameters) // 2
    v = {}

    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros_like(parameters['W' + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters['b' + str(l + 1)])

    return v


# parameters = initialize_velocity_test_case()
# v = initialize_velocity(parameters)
# print("v[\"dW1\"] = " + str(v["dW1"]))
# print("v[\"db1\"] = " + str(v["db1"]))
# print("v[\"dW2\"] = " + str(v["dW2"]))
# print("v[\"db2\"] = " + str(v["db2"]))


def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
    L = len(parameters) // 2
    for l in range(L):
        v["dW" + str(l + 1)] = beta * v["dW" + str(l + 1)] + (1 - beta) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta * v["db" + str(l + 1)] + (1 - beta) * grads['db' + str(l + 1)]
        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v["dW" + str(l + 1)]
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v["db" + str(l + 1)]

    return parameters, v


# parameters, grads, v = update_parameters_with_momentum_test_case()
# parameters, v = update_parameters_with_momentum(parameters, grads, v, beta=0.9, learning_rate=0.01)
# print("W1 = " + str(parameters["W1"]))
# print("b1 = " + str(parameters["b1"]))
# print("W2 = " + str(parameters["W2"]))
# print("b2 = " + str(parameters["b2"]))
# print("v[\"dW1\"] = " + str(v["dW1"]))
# print("v[\"db1\"] = " + str(v["db1"]))
# print("v[\"dW2\"] = " + str(v["dW2"]))
# print("v[\"db2\"] = " + str(v["db2"]))


def initialize_adam(parameters):
    L = len(parameters) // 2
    v = {}
    s = {}

    for l in range(L):
        v["dW" + str(l + 1)] = np.zeros_like(parameters['W' + str(l + 1)])
        v["db" + str(l + 1)] = np.zeros_like(parameters['b' + str(l + 1)])
        s["dW" + str(l + 1)] = np.zeros_like(parameters['W' + str(l + 1)])
        s["db" + str(l + 1)] = np.zeros_like(parameters['b' + str(l + 1)])

    return v, s


# parameters = initialize_adam_test_case()
# v, s = initialize_adam(parameters)
# print("v[\"dW1\"] = " + str(v["dW1"]))
# print("v[\"db1\"] = " + str(v["db1"]))
# print("v[\"dW2\"] = " + str(v["dW2"]))
# print("v[\"db2\"] = " + str(v["db2"]))
# print("s[\"dW1\"] = " + str(s["dW1"]))
# print("s[\"db1\"] = " + str(s["db1"]))
# print("s[\"dW2\"] = " + str(s["dW2"]))
# print("s[\"db2\"] = " + str(s["db2"]))


def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01,
                                beta1=0.9, beta2=0.999, epsilon=1e-8):
    L = len(parameters) // 2
    v_corrected = {}
    s_corrected = {}

    for l in range(L):
        v["dW" + str(l + 1)] = beta1 * v["dW" + str(l + 1)] + (1 - beta1) * grads['dW' + str(l + 1)]
        v["db" + str(l + 1)] = beta1 * v["db" + str(l + 1)] + (1 - beta1) * grads['db' + str(l + 1)]

        v_corrected["dW" + str(l + 1)] = v["dW" + str(l + 1)] / (1 - beta1 ** t)
        v_corrected["db" + str(l + 1)] = v["db" + str(l + 1)] / (1 - beta1 ** t)

        s["dW" + str(l + 1)] = beta2 * s["dW" + str(l + 1)] + (1 - beta2) * (grads["dW" + str(l + 1)]) ** 2
        s["db" + str(l + 1)] = beta2 * s["db" + str(l + 1)] + (1 - beta2) * (grads["db" + str(l + 1)]) ** 2

        s_corrected["dW" + str(l + 1)] = s["dW" + str(l + 1)] / (1 - beta2 ** t)
        s_corrected["db" + str(l + 1)] = s["db" + str(l + 1)] / (1 - beta2 ** t)

        parameters["W" + str(l + 1)] = parameters["W" + str(l + 1)] - learning_rate * v_corrected["dW" + str(l + 1)] / (
                np.sqrt(s_corrected["dW" + str(l + 1)]) + epsilon)
        parameters["b" + str(l + 1)] = parameters["b" + str(l + 1)] - learning_rate * v_corrected["db" + str(l + 1)] / (
                np.sqrt(s_corrected["db" + str(l + 1)]) + epsilon)

    return parameters, v, s


# parameters, grads, v, s = update_parameters_with_adam_test_case()
# parameters, v, s = update_parameters_with_adam(parameters, grads, v, s, t=2)
# print("W1 = " + str(parameters["W1"]))
# print("b1 = " + str(parameters["b1"]))
# print("W2 = " + str(parameters["W2"]))
# print("b2 = " + str(parameters["b2"]))
# print("v[\"dW1\"] = " + str(v["dW1"]))
# print("v[\"db1\"] = " + str(v["db1"]))
# print("v[\"dW2\"] = " + str(v["dW2"]))
# print("v[\"db2\"] = " + str(v["db2"]))
# print("s[\"dW1\"] = " + str(s["dW1"]))
# print("s[\"db1\"] = " + str(s["db1"]))
# print("s[\"dW2\"] = " + str(s["dW2"]))
# print("s[\"db2\"] = " + str(s["db2"]))


train_X, train_Y = load_dataset()


# print(train_X.shape)
# print(train_Y.shape)


def model(X, Y, layers_dims, optimizer, learning_rate=0.0007, mini_batch_size=64, beta=0.9,
          beta1=0.9, beta2=0.999, epsilon=1e-8, num_epochs=10000, print_cost=True):
    L = len(layers_dims)
    costs = []
    t = 0
    seed = 10

    parameters = initialize_parameters(layers_dims)

    if optimizer == "gd":
        pass
    elif optimizer == "momentum":
        v = initialize_velocity(parameters)
    elif optimizer == "adam":
        v, s = initialize_adam(parameters)

    for i in range(num_epochs):
        seed = seed + 1
        minibatches = random_mini_batches(X, Y, mini_batch_size, seed)

        for minibatch in minibatches:
            (minibatch_X, minibatch_Y) = minibatch

            # Forward propagation
            a3, caches = forward_propagation(minibatch_X, parameters)

            # Compute cost
            cost = compute_cost(a3, minibatch_Y)

            # Backward propagation
            grads = backward_propagation(minibatch_X, minibatch_Y, caches)

            # Update parameters
            if optimizer == "gd":
                parameters = update_parameters_with_gd(parameters, grads, learning_rate)
            elif optimizer == "momentum":
                parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
            elif optimizer == "adam":
                t = t + 1  # Adam counter
                parameters, v, s = update_parameters_with_adam(parameters, grads, v, s,
                                                               t, learning_rate, beta1, beta2, epsilon)

        if print_cost and i % 1000 == 0:
            print("Cost after epoch %i: %f" % (i, cost))
        if print_cost and i % 100 == 0:
            costs.append(cost)

    plt.plot(costs)
    plt.ylabel('cost')
    plt.xlabel('epochs (per 100)')
    plt.title("Learning rate = " + str(learning_rate))
    plt.show()

    return parameters


# layers_dims = [train_X.shape[0], 5, 2, 1]
# parameters = model(train_X, train_Y, layers_dims, optimizer="gd")
# predictions = predict(train_X, train_Y, parameters)
# plt.title("Model with Gradient Descent optimization")
# axes = plt.gca()
# axes.set_xlim([-1.5, 2.5])
# axes.set_ylim([-1, 1.5])
# plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

# layers_dims = [train_X.shape[0], 5, 2, 1]
# parameters = model(train_X, train_Y, layers_dims, beta=0.9, optimizer="momentum")
# predictions = predict(train_X, train_Y, parameters)
# plt.title("Model with Momentum optimization")
# axes = plt.gca()
# axes.set_xlim([-1.5, 2.5])
# axes.set_ylim([-1, 1.5])
# plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

layers_dims = [train_X.shape[0], 5, 2, 1]
parameters = model(train_X, train_Y, layers_dims, optimizer="adam")
predictions = predict(train_X, train_Y, parameters)
plt.title("Model with Adam optimization")
axes = plt.gca()
axes.set_xlim([-1.5, 2.5])
axes.set_ylim([-1, 1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)

---

三、总结

动量梯度下降通常是有用的，但由于给的是一个较小的学习率，并且数据集简单，它的影响几乎可以忽略不计。

再来看Adam，它的表现明显胜过小批量梯度下降和动量梯度下降。如果你在这个简单的数据集上运行更多次epochs，这三种方法都会带来非常好的结果。不过，你现在已经看到Adam更快地收敛了。

Adam的优势:

• 相对较低的内存需求（尽管高于梯度下降和动量梯度下降）。
• 即使是没有调优的超参数，该算法也能有比较好的结果。

各种优化算法比较：