【算法与数据结构】Python实现十三大查找和排序算法

本文讲解了十三个查找和排序算法的原理以及实现。码字不易，喜欢请点赞！！！有问题请留言，看到会回复，谢谢！！！

1.顺序查找
按照列表顺序挨个对比是否为目标值，知道找到，时间复杂度O(N)

nums = [4,7,12,20,36,48,50,77,90]
n = 36
for i in nums:
    if(i == n):
        print(i)
        break
#输出36

2.二分查找
列表是顺序列表，每次从中间值开始搜索，筛除一般，时间复杂度O(logN)

nums = [4,7,12,20,36,48,50,77,90]
n = 36
i = 0
j = len(nums)-1
while(i < j):
    mid = (i+j)//2
    if(nums[mid] == n):
        print(nums[mid])
        break
    elif(nums[mid] > n):
        j = mid - 1
    else:
        i = mid + 1
#输出36

3.Hash查找
根据索引直接查找，时间复杂度为O(1)
问题：Hash查找会出现冲突，解决方法线性探测法或其他方法

4.冒泡排序
每次比较临近两个值，互换位置，每次循环完最大值到最后位置。时间复杂度为O(n^2)。

nums = [77,4,20,90,36,12,7,50,48]
for i in range(len(nums)-1):
    for j in range(len(nums)-i-1):
        if(nums[j]>nums[j+1]):
            nums[j],nums[j+1] = nums[j+1],nums[j]
    print(nums)

从下面输出中可以看出后面几次都没有数据交换，因此可以改进。

[4, 20, 77, 36, 12, 7, 50, 48, 90]
[4, 20, 36, 12, 7, 50, 48, 77, 90]
[4, 20, 12, 7, 36, 48, 50, 77, 90]
[4, 12, 7, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]

5.短冒泡排序
冒泡排序的改进，当没有数据交换时，停止循环，方法也很简单，加一个Flag来判断是否进行了数据交换就行。时间复杂度小于O(n^2)。

nums = [77,4,20,90,36,12,7,50,48]
Flag = True
for i in range(len(nums)-1):
    Flag = False
    for j in range(len(nums)-i-1):
        if(nums[j]>nums[j+1]):
            nums[j],nums[j+1] = nums[j+1],nums[j]
            Flag = True
    print(nums)
    if(Flag == False):
        break

输出：

[4, 20, 77, 36, 12, 7, 50, 48, 90]
[4, 20, 36, 12, 7, 50, 48, 77, 90]
[4, 20, 12, 7, 36, 48, 50, 77, 90]
[4, 12, 7, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]

6.选择排序
冒泡排序中，每次发现相邻两个数据大小关系不对时，就进行数据交换，这样会带来很多数据交换的代价，因此可以减少交换次数，每次选择最大值，直接跟最后位置交换，从而减少数据交换。时间复杂度为O(n^2)。

nums = [77,4,20,90,36,12,7,50,48]
for i in range(len(nums)-1):
    k = 0
    for j in range(1,len(nums)-i):
        if(nums[k] < nums[j]):
            k = j
    nums[k],nums[j] = nums[j],nums[k]
    print(nums)

输出：

[77, 4, 20, 48, 36, 12, 7, 50, 90]
[50, 4, 20, 48, 36, 12, 7, 77, 90]
[7, 4, 20, 48, 36, 12, 50, 77, 90]
[7, 4, 20, 12, 36, 48, 50, 77, 90]
[7, 4, 20, 12, 36, 48, 50, 77, 90]
[7, 4, 12, 20, 36, 48, 50, 77, 90]
[7, 4, 12, 20, 36, 48, 50, 77, 90]
[4, 7, 12, 20, 36, 48, 50, 77, 90]

7.插入排序
插入排序的思想是在一个已经有序的数据序列上插入一个数，插入之后这个数据序列依旧有序。算法适用于少量数据的排序，时间复杂度为O(n^2)。

nums = [77,4,20,90,36,12,7,50,48]
for i in range(1,len(nums)):
    current = nums[i]
    j = i
    while(j>0 and current<nums[j-1]):
        nums[j] = nums[j-1]
        j = j -1
    nums[j] = current
    print(nums)

输出：

[4, 77, 20, 90, 36, 12, 7, 50, 48]
[4, 20, 77, 90, 36, 12, 7, 50, 48]
[4, 20, 77, 90, 36, 12, 7, 50, 48]
[4, 20, 36, 77, 90, 12, 7, 50, 48]
[4, 12, 20, 36, 77, 90, 7, 50, 48]
[4, 7, 12, 20, 36, 77, 90, 50, 48]
[4, 7, 12, 20, 36, 50, 77, 90, 48]
[4, 7, 12, 20, 36, 48, 50, 77, 90]

8.希尔排序
插入排序的改进，也称为“递增递减排序”，将原始列表分解为多个较小的子列表来改进插入排序，每个子列表使用插入排序进行排序。
网络上有个描述这个过程的图，很形象：

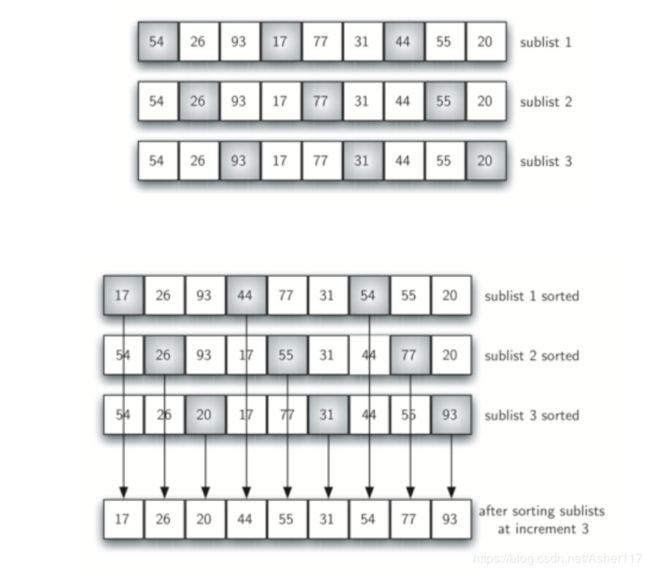
9.归并排序
将列表拆分成左右两边，然后将左右两边继续拆分，直至长度为1，然后合并。时间复杂度为O(nlogn)。问题：需要额外的空间来存储左右两边的列表

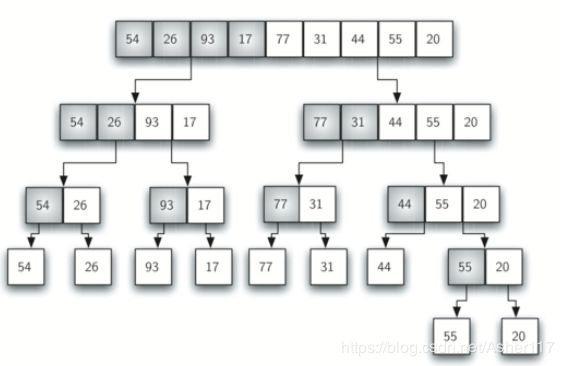
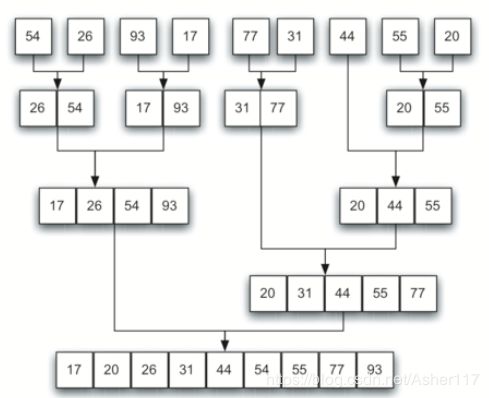
def mergeSort(alist):
    print("Splitting:",alist)
    if(len(alist)>1):
        mid = len(alist)//2
        lefthalf = alist[:mid]
        righthalf = alist[mid:]
        
        mergeSort(lefthalf)
        mergeSort(righthalf)
        
        i,j,k = 0,0,0
        while(i<len(lefthalf) and j < len(righthalf)):
            if(lefthalf[i]<righthalf[j]):
                alist[k] = lefthalf[i]
                i = i + 1
            else:
                alist[k] = righthalf[j]
                j = j + 1
            k = k + 1
        while(i<len(lefthalf)):
            alist[k] = lefthalf[i]
            i = i + 1
            k = k + 1
        while(j<len(righthalf)):
            alist[k] = righthalf[j]
            j = j + 1
            k = k + 1
    print("Merging ",alist)
 
alist = [54,26,93,17,77,31,44,55,20]
mergeSort(alist)

10.快速排序
归并排序的改进，不需要额外的空间。 O(nlogn），但如果分割点不在列表中间附近，可能会降级到O(n^2 )
它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。
过程如下如图：

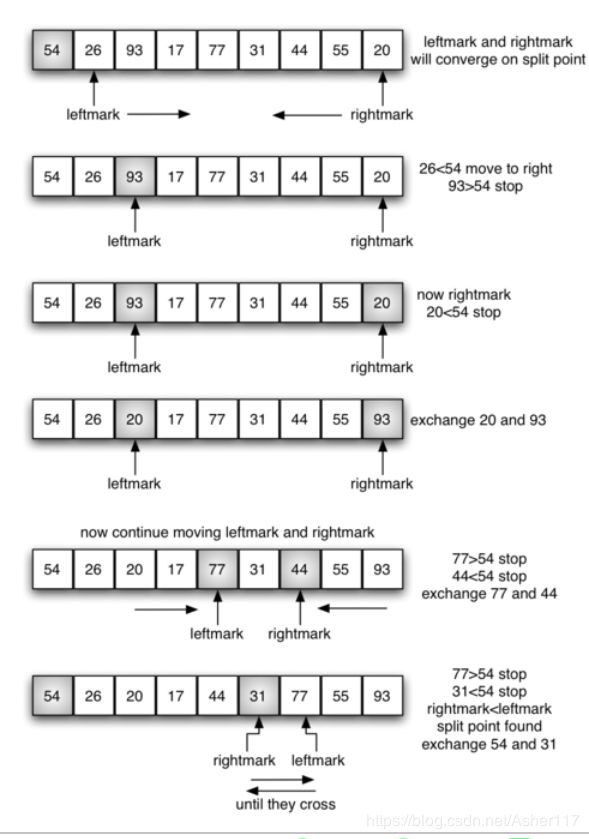
一次排序之后结果：

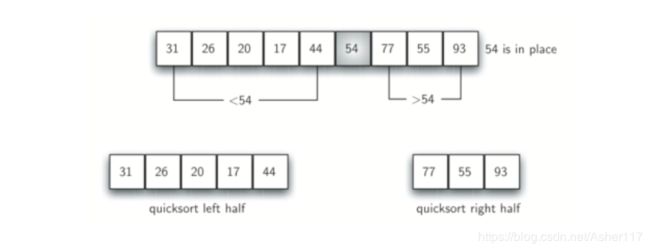
实现：递归+分而治之

def sort(nums):
    if(len(nums)<=1):
        return nums 
    else:
        mid = nums[0]
        left = []
        right = []
        for i in nums[1:]:
            if(i > mid):
                right.append(i)
            else:
                left.append(i)
        return sort(left) + [mid] + sort(right)
nums = [77,4,20,90,36,12,7,50,48]
sort(nums)

结果：

[4, 7, 12, 20, 36, 48, 50, 77, 90]

11.【其他】二叉排序树

12.【其他】堆排序

13.基数排序
基数排序属于分配排序，又称为桶子法。基数排序法是属于稳定性的排序，其时间复杂度为$O(nlo{g}_r^m)$，其中r为所采取的基数，而m为堆数。
【基本解法】
第一步
以LSD为例，假设原来有一串数值如下所示：
73, 22, 93, 43, 55, 14, 28, 65, 39, 81
首先根据个位数的数值，在走访数值时将它们分配至编号0到9的桶子中：
0
1 81
2 22
3 73 93 43
4 14
5 55 65
6
7
8 28
9 39
第二步
接下来将这些桶子中的数值重新串接起来，成为以下的数列：
81, 22, 73, 93, 43, 14, 55, 65, 28, 39
接着再进行一次分配，这次是根据十位数来分配：
0
1 14
2 22 28
3 39
4 43
5 55
6 65
7 73
8 81
9 93
第三步
接下来将这些桶子中的数值重新串接起来，成为以下的数列：
14, 22, 28, 39, 43, 55, 65, 73, 81, 93
这时候整个数列已经排序完毕；如果排序的对象有三位数以上，则持续进行以上的动作直至最高位数为止。
LSD的基数排序适用于位数小的数列，如果位数多的话，使用MSD的效率会比较好。MSD的方式与LSD相反，是由高位数为基底开始进行分配，但在分配之后并不马上合并回一个数组中，而是在每个“桶子”中建立“子桶”，将每个桶子中的数值按照下一数位的值分配到“子桶”中。在进行完最低位数的分配后再合并回单一的数组中。