NOIP2017赛前模拟（2017.10.20）Matrix （类似轮廓线DP）

题意：
　给一个N行M列的矩阵，挑出K个互不重叠的子矩阵，得分为这些子矩阵中的数值和，求这个数值的最大值。
题解：
　因为数据范围为：1<=N<=100,1<=M<=2,1<=K<=10,|数值|<=1000000;
　虽然有( n3 k)比较明显的DP，还是有(nk)的DP，类似于轮廓线DP；因为M<=2,所以我们每次DP是一共有五种状态：

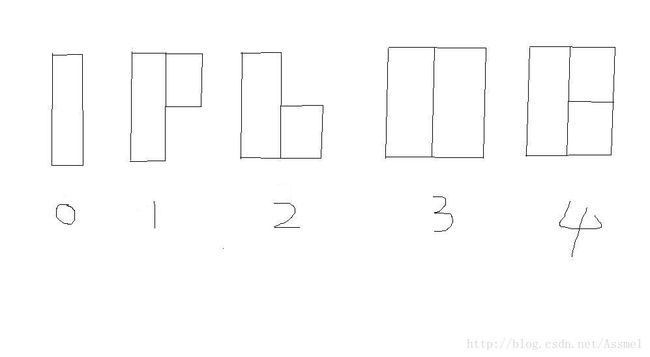
0—当前这一行不选；
1—当前这一行选第一列；
2—当前这一行选第二列；
3—当前这一行两个都选，而且属于同一矩阵；
4—当前这一行两个都选，但属于不同矩阵

由此我们就可以定义 f[ i ][ k ][ 5 ]表示前I行，选了K个矩阵，当前状态为0/1/2/3/4,就可以转移了

#include
#include
#include
#include
#include
#include
#include
#include
#include
using namespace std;
int n,m,k,ans,f=1,a[205][5];
inline int Readint(){
    int x=0,p=1;
    char c=getchar();
    while(!isdigit(c)){
        if(c=='-') p=-1;
        c=getchar();
    }
    while(isdigit(c)){
        x=(x<<1)+(x<<3)+(c^'0');
        c=getchar();
    }
    return x*p;
}

inline void work1(){
    static int f[205][20][5];
    memset(f,128,sizeof(f));
    f[0][0][0]=f[0][0][1]=0;
    for(int i=1;i<=n;i++){
        f[i][0][0]=0;
        for(int j=1;j<=k;j++){
            f[i][j][0]=max(f[i-1][j][0],f[i-1][j][1]);
            f[i][j][1]=max(f[i-1][j-1][0]+a[i][1],max(f[i-1][j][1]+a[i][1],f[i-1][j-1][1]+a[i][1]));
        }
    }
    ans=-0x3fffffff;
    for(int i=1;i<=n;i++)
      ans=max(ans,max(f[i][k][0],f[i][k][1]));
    cout<void work2(){
    static int f[205][20][8];
    memset(f,128,sizeof(f));
    f[0][0][0]=0;
    for(int i=1;i<=n;i++){
        f[i][0][0]=0;
        for(int j=1;j<=k;j++){
            f[i][j][0]=max(f[i-1][j][0],max(f[i-1][j][1],max(f[i-1][j][2],max(f[i-1][j][3],f[i-1][j][4])))); //当前这一行不选 

            f[i][j][1]=a[i][1]+max(f[i-1][j-1][0],max(f[i-1][j-1][1],max(f[i-1][j-1][2],max(f[i-1][j-1][3],f[i-1][j-1][4]))));//当前这一行单独开始一个矩阵
            f[i][j][1]=max(f[i][j][1],a[i][1]+max(f[i-1][j][1],f[i-1][j][4]));//与上一行接上成为一个矩阵

            f[i][j][2]=a[i][2]+max(f[i-1][j-1][0],max(f[i-1][j-1][1],max(f[i-1][j-1][2],max(f[i-1][j-1][3],f[i-1][j-1][4])))); 
            f[i][j][2]=max(f[i][j][2],a[i][2]+max(f[i-1][j][2],f[i-1][j][4]));

            f[i][j][3]=a[i][1]+a[i][2]+max(f[i-1][j-1][0],max(f[i-1][j-1][1],max(f[i-1][j-1][2],max(f[i-1][j-1][3],f[i-1][j-1][4]))));
            f[i][j][3]=max(f[i][j][3],a[i][1]+a[i][2]+f[i-1][j][3]);

            if(j>=2) f[i][j][4]=a[i][1]+a[i][2]+max(f[i-1][j-2][0],max(f[i-1][j-2][1],max(f[i-1][j-2][2],max(f[i-1][j-2][3],f[i-1][j-2][4]))));
            f[i][j][4]=max(f[i][j][4],a[i][1]+a[i][2]+max(f[i-1][j-1][1],max(f[i-1][j-1][2],f[i-1][j-1][4])));
            f[i][j][4]=max(f[i][j][4],a[i][1]+a[i][2]+f[i-1][j][4]);
        }
    }
    ans=-0x3fffffff;
    for(int i=1;i<=n;i++)
      ans=max(ans,max(f[i][k][0],max(f[i][k][1],max(f[i][k][1],max(f[i][k][2],max(f[i][k][3],f[i][k][4]))))));
    cout<int main(){
//  freopen("matrix.in","r",stdin);
    n=Readint(),m=Readint(),k=Readint();
    for(int i=1;i<=n;i++)
        for(int j=1;j<=m;j++){
            a[i][j]=Readint();
            if(a[i][j]<0) f=0;
            ans+=a[i][j];
        }
    if(f){
        cout<return 0;
    }
    if(m==1) work1();
    else work2();
    return 0;
}