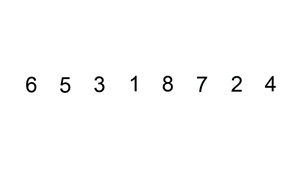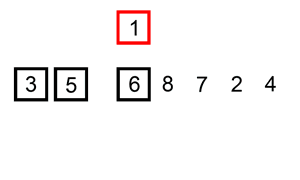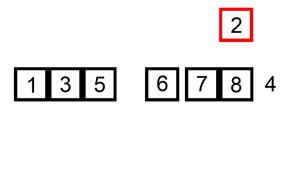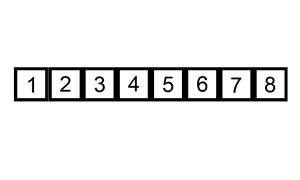8 大内部排序算法相关及其java实现

ps:本博文主要内容来自：www.cricode.com/3212.html，博主添加了算法的适用场景、分类、java实现相关模块，并对内容进行了一些修改。如有不足之处，请不吝指教。

首先，排序算法可以分为内部排序和外部排序，内部排序是数据记录在内存中进行排序，而外部排序是因排序的数据很大，一次不能容纳全部的排序记录，在排序过程中需要访问外存。

    常见的内部排序算法有：插入排序、希尔排序、选择排序、冒泡排序、归并排序、快速排序、堆排序、基数排序等。

    外部排序的算法有：常用多路归并排序等，在此不做介绍。

---

本文将依次介绍上述八大内部排序算法。

算法一：插入排序

插入排序是一种最简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

算法步骤：

1）将第一待排序序列第一个元素看做一个有序序列，把第二个元素到最后一个元素当成是未排序序列。

2）从头到尾依次扫描未排序序列，将扫描到的每个元素插入有序序列的适当位置。（如果待插入的元素与有序序列中的某个元素相等，则将待插入元素插入到相等元素的后面。）

适用场景：

    适用于小数据量并且已经基本有序的数据（此处基本有序代表正序，即想要递增的结果，则数组基本递增s有序），插入排序可以明显减少数据交换和数据移动次数，进而提升排序效率。

算法实现：

 

package arithmetic;

/**

* 插入排序java实现

*/

public class InsertSort {
    static void insertSort(int [] datas) throws Exception {
        //异常处理
        if (datas.length == 0){
            throw new Exception("接收到空数组！！");
        }   
        int len = 1;
        //遍历旧数组中的数据
        for (int i = 1; i < datas.length; i++) {
            int num = datas[i];
            //便利新数组中的数据，进行插入
            for (int j = 0; j < len; j++) {
                //如果满足条件进行插入
                if (num <= datas[j]){
                    for (int k = len; k > j; k--) {
                    datas[k] = datas[k-1];
                    }
                    datas[j] = num;
                    break;
                }else if (j == len-1){
                    datas[j+1] = num;
                }
            }
            len++;
        }
    }


    public static void main(String[] args) throws Exception {
        int [] datas = {4,2,87,4,2,7,9,6,3,7};
        System.out.println(Arrays.toString(datas));
        //异常处理也可在此处进行处理，接受上层传过来的异常并进行处理
        //使用希尔排序进行排序
        System.out.println();
        insertSort(datas);
       System.out.println(Arrays.toString(datas));
    }

}

---

算法二：希尔排序

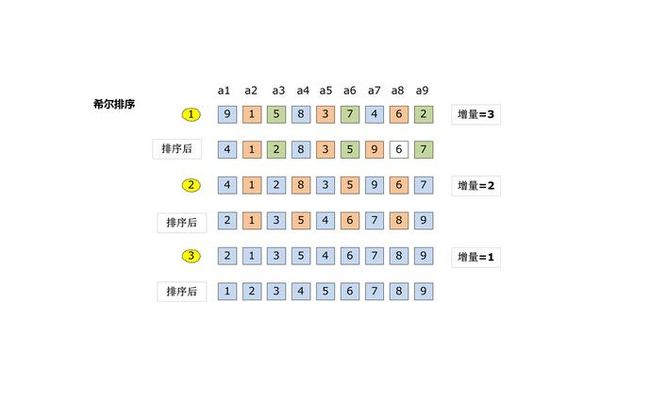
希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本。但希尔排序是非稳定排序算法。

希尔排序是基于插入排序的以下两点性质而提出改进方法的：

• 插入排序在对几乎已经排好序的数据操作时， 效率高， 即可以达到线性排序的效率

• 但插入排序一般来说是低效的， 因为插入排序每次只能将数据移动一位

希尔排序的基本思想是：先将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，待整个序列中的记录“基本有序”时，再对全体记录进行依次直接插入排序。点击这里了解常用的加密算法。

算法步骤：

1）选择一个增量序列t1，t2，…，tk，其中ti>tj，tk=1；

2）按增量序列个数k，对序列进行k 趟排序；

3）每趟排序，根据对应的增量ti，将待排序列分割成若干长度为m 的子序列，分别对各子表进行直接插入排序。仅增量因子为1 时，整个序列作为一个表来处理，表长度即为整个序列的长度。

适用场景：

    比较在希尔排序中是最主要的操作，而不是交换。”用已知最好的（Sedgewick提出的）步长序列的希尔排序比直接插入排序要快，甚至在小数组中比快速排序和堆排序还快，但是在涉及大量数据时希尔排序还是比快速排序慢。

    因为增量初始值不容易选择，所以该算法不常用。

算法实现：

package arithmetic;

/**
* 希尔排序java实现
*/
public class ShellSort {
    static void shellSort(int[] datas) throws Exception{
        //异常处理
        if (datas.length==0){
            throw new Exception("接收到空数组，请传入非空数组！");
        }
        int len = datas.length;
        int d = len;
        //希尔排序的间隔    
        while(d > 1){
            //取上一次的二分之一
            d = (d+1)>>1;
            //循环到len-d即可，因为后面没有可匹配的
            for (int i = 0; i < len-d; i++) {
                if (datas[i]>datas[i+d]){
                int temp = datas[i+d];
                datas[i+d] = datas[i];
                datas[i] = temp;
                }
           }
        }
        System.out.println();
        System.out.println(Arrays.toString(datas));
    }

    public static void main(String[] args) throws Exception {
        int [] datas = {4,2,87,4,2,7,9,6,3,7};
        System.out.println(Arrays.toString(datas));
        //异常处理也可在此处进行处理，接受上层传过来的异常并进行处理        
        //使用希尔排序进行排序
        shellSort(datas);
    }
}

---

算法三：选择排序

选择排序(Selection sort)也是一种简单直观的排序算法。

算法步骤：

1）首先在未排序序列中找到最小（大）元素，存放到排序序列的起始位置

2）再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。

3）重复第二步，直到所有元素均排序完毕。

适用场景：

    不管数据是否基本有序，在每次取最小值的时候都会进行全部比较。所以更加适合数据量小，无法确定数据是否有序的时候。

算法实现：

package arithmetic;

/**
* 选择排序java实现
*/
public class ChooseSort {
    static void chooseSort(int[] datas) throws Exception {
        //异常处理
        if (datas.length <= 0){
            throw new Exception("接收到空数组！！");
        }
        int min_index;
        //循环数组中所有数据
        for (int i = 0; i < datas.length; i++) {
            min_index = i;
            //获得最小值下标
            for (int j = i+1; j < datas.length; j++) {
                if (datas[j] < datas[min_index])
                    min_index = j;
            }
            //将最小值与已排序好部分的下一个元素交换位置 （实现在一个数组中完成排序，不需要重建数组）
            int temp = datas[i];
            datas[i] = datas[min_index];
            datas[min_index] = temp;
        }
    }

    public static void main(String[] args) throws Exception {
        int[] datas = {4,2,87,4,2,7,9,6,3,7};
        System.out.println(Arrays.toString(datas));
        System.out.println();
        //异常处理也可在此处进行处理，接受上层传过来的异常并进行处理
        //使用选择排序进行排序
        chooseSort(datas);
        System.out.println(Arrays.toString(datas));
    }
}

---

算法四：冒泡排序

冒泡排序（Bubble Sort）也是一种简单直观的排序算法。它重复地走访过要排序的数列，一次比较两个元素，如果他们的顺序错误就把他们交换过来。走访数列的工作是重复地进行直到没有再需要交换，也就是说该数列已经排序完成。这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端。点击这里了解常用的加密算法。

算法步骤：

1）比较相邻的元素。如果第一个比第二个大，就交换他们两个。

2）对每一对相邻元素作同样的工作，从开始第一对到结尾的最后一对。这步做完后，最后的元素会是最大的数。

3）针对所有的元素重复以上的步骤，除了最后一个。

4）持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

适用场景：

    适用于数据初始状态基本有序，此处基本有序代表正序，即想要递增的结果，则数组基本递增s有序。

算法实现：

package arithmetic;

/**
* 冒泡排序java实现
*/
public class BubbleSort {

    static void bubbleSort(int[] datas) throws Exception {
        //异常处理
        if (datas.length <= 0){
            throw new Exception("接收到空数组！！");
        }
        int k = datas.length; //用来提高冒泡排序效率，指向每轮排序的最后一个交换的位置
        int m;
        //循环比较直到满足break;条件
        while(k > 0) {
            m = k;
            for (int i = 0; i < m - 1; i++) {
                if (datas[i] > datas[i + 1]) {
                    int temp = datas[i];
                    datas[i] = datas[i + 1];
                    datas[i + 1] = temp;
                    k = i+1;
                }
            }
            //如果此轮没有交换的数据，说明顺序一致，直接退出。如果有，则m和一定不一致，则继续循环
            if (m == k)
               break;
        }
    }

    public static void main(String[] args) throws Exception {
        int[] datas = {4,2,87,4,2,7,9,6,3,7};
        //打印未排序前数组
        System.out.println(Arrays.toString(datas));
        System.out.println();
        //异常处理也可在此处进行处理，接受上层传过来的异常并进行处理
        //使用选择排序进行排序
       int[] new_datas = bubbleSort(datas);
       System.out.println(Arrays.toString(datas));
    }
}

---

算法五：归并排序

归并排序（Merge sort）是建立在归并操作上的一种有效的排序算法。该算法是采用分治法（Divide and Conquer）的一个非常典型的应用。

算法步骤：

1. 申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列

2. 设定两个指针，最初位置分别为两个已经排序序列的起始位置

3. 比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置

4. 重复步骤3直到某一指针达到序列尾

5. 将另一序列剩下的所有元素直接复制到合并序列尾

如：（此处来自百度百科）

设有数列{6，202，100，301，38，8，1}

初始状态：6,202,100,301,38,8,1

第一次归并后：{6,202},{100,301},{8,38},{1}，比较次数：3；

第二次归并后：{6,100,202,301}，{1,8,38}，比较次数：4；

第三次归并后：{1,6,8,38,100,202,301},比较次数：4；

总的比较次数为：3+4+4=11；

适用场景：

 其时间复杂度为： O(nlog2(n)) ，所以适合数据量较大，有需要排序稳定的需求的时候。

算法实现：

 

package arithmetic;

import java.util.Arrays;

/**
* 二路归并排序算法java实现
*/
public class MegerSort {
    private static void sort(int[] datas, int start, int end) throws Exception {
        //异常处理
        if (datas.length == 0){
            throw new Exception("接收到空数组！！");
        }
        if (start >= end)
            return;
        //取中间位置为分割点
        int mid = (start + end) >> 1;
        /**
        * 递归实现
        * 1.递归过程直到start >= end
        * 2.递归到底时，开始进行二路归并mergerSort
        */
        sort(datas, start, mid);
        sort(datas, mid + 1, end);
        mergerSort(datas, start, mid, end);
    }

    // 将两个有序序列归并为一个有序序列(二路归并)
    private static void mergerSort(int[] datas, int start, int mid, int end) {
        int[] arr = new int[end + 1]; // 定义一个临时数组，用来存储排序后的结果
        int low = start; // 临时数组的索引
        int left = start;
        int center = mid + 1;
        // 取出最小值放入临时数组中
        while (start <= mid && center <= end) {
            arr[low++] = datas[start] > datas[center] ? datas[center++] : datas[start++];
        }

        // 若还有段序列不为空，则将其加入临时数组末尾
        while (start <= mid) {
            arr[low++] = datas[start++];
        }
        while (center <= end) {
            arr[low++] = datas[center++];
        }

        // 将临时数组中的值copy到原数组中
        for (int i = left; i <= end; i++) {
            datas[i] = arr[i];
        }
    }

    public static void main(String[] args) throws Exception {
        int[] datas = {4,2,87,4,2,7,9,6,3,7};
        System.out.println(Arrays.toString(datas));
        System.out.println();
        //异常处理也可在此处进行处理，接受上层传过来的异常并进行处理
        //使用归并排序进行排序
        sort(datas,0,datas.length-1);
        System.out.println(Arrays.toString(datas));
    }
}

---

算法六：快速排序

快速排序是由东尼·霍尔所发展的一种排序算法。在平均状况下，排序 n 个项目要Ο(n log n)次比较。在最坏状况下则需要Ο(n2)次比较，但这种状况并不常见。事实上，快速排序通常明显比其他Ο(n log n) 算法更快，因为它的内部循环（inner loop）可以在大部分的架构上很有效率地被实现出来。

快速排序使用分治法（Divide and conquer）策略来把一个串行（list）分为两个子串行（sub-lists）。

算法步骤：

1 从数列中挑出一个元素，称为 “基准”（pivot），

2 重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作。

3 递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

递归的最底部情形，是数列的大小是零或一，也就是永远都已经被排序好了。虽然一直递归下去，但是这个算法总会退出，因为在每次的迭代（iteration）中，它至少会把一个元素摆到它最后的位置去。

简介相关： https://baike.baidu.com/item/%E5%BF%AB%E9%80%9F%E6%8E%92%E5%BA%8F%E7%AE%97%E6%B3%95/369842?fr=kg_qa#4

时间复杂度分析：https://www.cnblogs.com/pugang/archive/2012/07/02/2573075.html

适用场景：

    适合大数据量，不要求排序稳定，待排序的关键字是随机分布时。是目前基于比较的内部排序中被认为是最好的方法。

算法实现：

package arithmetic;

public class QuickPaixvTest {

    static int nums[] = {4,2,78,342,123,543,6,311,2};

    public static void main(String[] args) {
        System.out.print("原数组： ");
        for (int i = 0; i < nums.length; i++) {
            System.out.print(nums[i]+" ");
        }
        fastSort(0,nums.length-1,nums);
        System.out.println();
        System.out.print("排序后数组： ");
        for (int i = 0; i < nums.length; i++) {
            System.out.print(nums[i]+" ");
        }
    }

    static void fastSort(int low ,int high ,int[] nums){
        //异常
        if (nums.length == 0)
            throw new NegativeArraySizeException("数组为空！");
        if (low < 0 || high < 0 || high >= nums.length || low >= nums.length)
            throw new ArrayIndexOutOfBoundsException("请输入正确的数组下标！");
        int i = low;
        int j = high;
        int key = nums[low];
        //配合其中的两个while可达到左边右边循环比较的效果
        while(i i && nums[j] >= key){
                j--;
            }
            //用if判断一下为了避免上述循环时因为不满足第一个条件而退出的
            if (key >= nums[j]){
                 /**交换*/
                int tem = nums[j];
                nums[j] = nums[i];
                nums[i] = tem;
            }
            //从左边比较
            while (j > i && nums[i] <= key){
                i++;
            }
            if (nums[i] >= key){
                /**交换*/
                int tem = nums[j];
                nums[j] = nums[i];
                nums[i] = tem;
            }
        }
        if (i>low) fastSort(low,i-1,nums);
        if (j

---

算法七：堆排序

堆排序（Heapsort）是指利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。

堆排序的平均时间复杂度为Ο(nlogn) 。

分为：大根堆排序，小根堆排序

算法步骤：

1）创建一个堆H[0..n-1]

2）把堆首（最大值）和堆尾互换

3）把堆的尺寸缩小1，并调用shift_down(0)，目的是把新的数组顶端数据调整到相应位置

4） 重复步骤2，直到堆的尺寸为1

详解：https://blog.csdn.net/CSDN___LYY/article/details/81454613

适用场景：

    适用于内存要求严格，数据量大，不要求排序稳定的时候。堆排序所需的辅助空间少于快速排序,并且不会出现快速排序可能出现的最坏情况。

算法实现：（大根堆，递增顺序）

package arithmetic;

import java.util.Arrays;

/**
* 堆排序java实现
*/
public class HeapSort {
    static int k = 0; //全局k,用于排序一次后获得一个最大的，需要数组的size-1
    public static void main(String[] args) {
        int[] datas = {4,2,87,4,2,7,9,6,3,7};
        System.out.println(Arrays.toString(datas));
        //初始化堆
        buildHeap(datas);
        //进行排序
        for (int i = datas.length-1; i > 0 ; i--) {
            //堆顶的最大值与数组的最后一个元素交换（此处为k存在的原因）
            int temp = datas[i];
            datas[i] = datas[0];
            datas[0] = temp;
            k++; //使数组的size-1
            //调整堆
            adjustHeap(datas,0);
        }
        System.out.println(Arrays.toString(datas));
    }

    /**
    * 初始化堆
    * @param datas 需被初始化的数组
    */
    static void buildHeap(int[] datas){
        // i = (datas.length-1)>>1 ：找到最后一个父结点，之后往前循环调整堆
        for (int i = (datas.length-1)>>1; i >= 0; i--) {
           adjustHeap(datas,i);
        }
    }
    /**
    * 调整堆
    * @param datas 需被调整的堆
    * @param i 调整元素所在的位置
    */
    static void adjustHeap(int[] datas , int i){
        //循环，使可以调整到底部
        while(true){
            int left = (i<<1)+1; //左孩子
            int right = (i<<1)+2; //右孩子

            int largest = i; //标识自身和孩子中，最大值的下标
            if (left < datas.length-k && datas[i] < datas[left]){
                largest = left;
            }

            if (right < datas.length-k && datas[largest] < datas[right]){
                largest = right;
            }

            //如果满足条件，表示最大的不是节点自身，则交换
            if (largest != i){
                int temp = datas[i];
                datas[i] = datas[largest];
                datas[largest] = temp;
            }else{ //否则，退出循环
                // 原因：因为是从最下面开始进行调整的，所以我们可以只要最大节点是节点自身，我们就可以直接退出
                return;
            }
            i = largest; //修改自身节点
        }
    }
}

---

算法八：基数排序

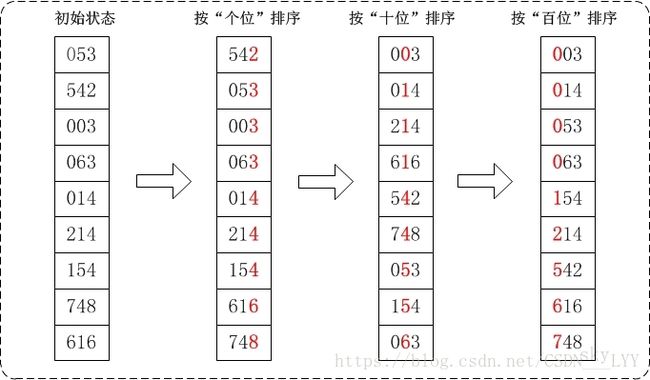
    基数排序是一种非比较型整数排序算法，其原理是将整数按位数切割成不同的数字，然后按每个位数分别比较。由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也不是只能使用于整数。

    数组{53, 3, 542, 748, 14, 214, 154, 63, 616}排序的过程图：（来自网络）

    前面说的几大排序算法 ，大部分时间复杂度都是O（n2），也有部分排序算法时间复杂度是O(nlogn)。而桶式排序却能实现O（n）的时间复杂度。但桶排序的缺点是：

    1）首先是空间复杂度比较高，需要的额外开销大。排序有两个数组的空间开销，一个存放待排序数组，一个就是所谓的桶，比如待排序值是从0到m-1，那就需要m个桶，这个桶数组就要至少m个空间。

    2）其次待排序的元素都要在一定的范围内等等。

---

总结

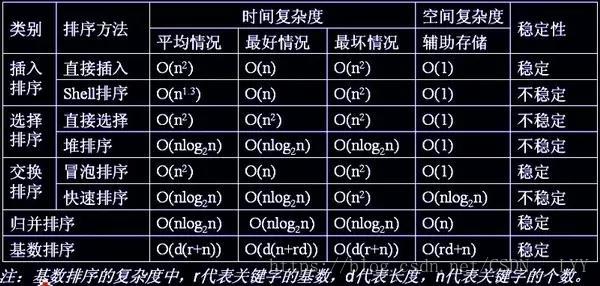
各种排序的稳定性，时间复杂度、空间复杂度、稳定性总结如下图：

分类：

（1）插入排序法

    直接插入排序，希尔排序

（2）交换排序

    冒泡排序，快速排序

（3）选择排序

    直接选择排序，堆排序

（4）归并排序

     归并排序

（5）基数排序

关于时间复杂度：

(1)平方阶(O(n2))排序各类简单排序：直接插入、直接选择和冒泡排序；

(2)线性对数阶(O(nlog2n))排序快速排序、堆排序和归并排序；

(3)O(n1+§))排序，§是介于0和1之间的常数。希尔排序

(4)线性阶(O(n))排序基数排序，此外还有桶、箱排序。

关于稳定性：（ 稳定性是指如果存在多个具有相同值的记录，经过排序后，这些记录的相对次序仍然保持不变，则这种排序算法称为稳定的）

稳定的排序算法：冒泡排序、插入排序、归并排序和基数排序

不是稳定的排序算法：选择排序、快速排序、希尔排序、堆排序