有意思的kd树
每一个空间就像超级玛丽里面的不同游戏区域。(虽然这个比喻能和kd树划分超平面(hyperplane)对应上的不多)
---------------------------------------kd树自问自答---------------------------------------
我在有点理解kd树的时候(完全理解kd树之前),有一些疑惑和误解:
问:如何保证某个点所在的最小空间边界上的点是所有点中离它最近的点?
答:kd树从来没有保证过这一点,也不是这么用的。它只是一个数据点的组织形式。kd树中位于(以数据点为中心的)超球体内的数据点才是候选点。
kd树循环比较不同的特征维度这种设定背后的原理是什么?有什么好处?
答:kd树的默认距离计算方法是欧氏距离。(用某一个坐标轴的减去法,代替空间的点的距离计算)
问:它最近的点都在从叶结点到根结点的路径上吗?
答:并没有直接关系。这个需要看在搜索过程中,(程不增趋势的)超球面所包含的kd树的划分都是搜索范围。
确定后candidate hypersphere后,是怎样找到包含在所有超球面里的点的呢?kd树在这个过程中起到什么优化作用呢?停止搜索的条件又是什么呢?
答:确定超平面后,并不穷举超球面里面的点。超球面只是用于限定范围。只搜索,在超球体中且在kd树中且未被搜索到的分枝。
答:kd树应该是起到一个数据点的空间组织形式吧。
答:整个搜索过程是一个递归过程,从根结点开始,到根结点结束。
超球面是如何剪枝(prune)的呢?
答:整个搜索过程,超球体是在不断减小(或者说不增大)的过程。在搜索过程中,如果在测试点一侧的划分结束后,球面仍然伸展到了测试不包含测试点的另一侧,则断续向另一侧搜索。
------------------------------------------kd树知识点理解------------------------------------------
kd树中的『k』指的表示每个样本(observation)的向量的维度。这个和k-means是不一样的。(kd-tree, short for k-dimensional tree)。
kd树不能保存strings。
kd树的每一个结点的维度必须相同。(例如,一个存储四维结点的kd树,不能用于保存二维结点)。
kd树是一个二叉树,它使用与轴线对齐(可理解为与一个轴线平行,与另一个垂直)的超平面(可理解为一维中的点,二维中的线,三维中的面,四维就不知道了。。)将点集中的点划分到超空间(如三维空间)的子空间中(一个小长方体,里面有一个点),而形成的一个存在于超空间中的、由子空间形成的层次结构。
每一个叶子结点都是数据点(可能包含少量几个数据点,这个要看划分力度)。
这种设定,巧妙地处理了空间的几何划分关系。利用这种设定,我们就不需要额外写代码来保持每次划分时的划分超平面的定义。
用每个维度的中位数划分会形成一个平衡二叉树,有许多优良的特性,但会增加一些计算量。而且,平衡二叉树未必是最优的二叉树。
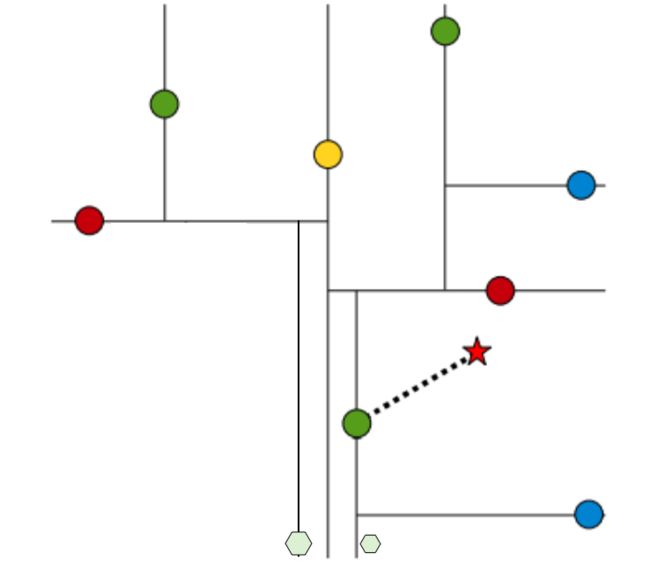
------------------------------------------kd树图例------------------------------------------
------------------------------------------1-nearest-----------------------------------------
------------------------------------------K-nearest-----------------------------------------
1-nearest我知道了,那么怎么推广到K呢?
看过了stanford的提示,我的想法如下:
在1-nearest基础上,maintain(维持)一个K维,初始化全为infinit的数组(表示K个最近邻点)
并且,这个K维数组最好是有序的(按照与test point 的距离排出)。这样,K个待选点的candidate sphere就是以测试点(test point)为中心,以K维数组中与test point 最远点的距离为半径的超球面里面了。然后搜索完这个范围,以搜索完这个kd树结束。
参考:
http://www.cs.princeton.edu/courses/archive/spr13/cos226/lectures/99GeometricSearch.pdf
https://en.wikipedia.org/wiki/K-d_tree
《统计学习方法》李航
python实现:https://github.com/stefankoegl/kdtree.git
斯坦福C++作业3:http://web.stanford.edu/class/cs106l/handouts/assignment-3-kdtree.pdf