基于支持向量机(SVM)的遗传疾病致病位点预测分析
[项目实现程序的github仓库]
(https://github.com/MichealCarol/Prediction-Analysis-of-Pathogenic-Sites-of-Genetic-Diseases-Based-on-SVM.git)
1 问题描述
近年来,随着计算机应用技术的发展以及大数据时代的到来,人们对人体基因与遗传性疾病的研究越来越深入了。研究人员大都采用全基因组的方法来确定致病位点或致病基因,具体做法是:招募大量志愿者(样本),包括具有某种遗传病的人和健康的人,通常用1表示病人,0表示健康者。 对每个样本,采用碱基(A,T,C,G)的编码方式来获取每个位点(在组成DNA的数量浩瀚的碱基对中,有一些特定位置的单个核苷酸经常发生变异引起DNA的多态性,我们称之为位点,染色体、基因和位点的结构关系见图1.)的信息(因为染色体具有双螺旋结构,所以用两个碱基的组合表示一个位点的信息);如表1中,在位点rs100015位置,不同样本的编码都是T和C的组合,有三种不同编码方式TT,TC和CC。研究人员可以通过对样本的健康状况和位点编码的对比分析来确定致病位点,从而发现遗传病或性状的遗传致病机理。(此问题改编自2016年全国研究生数学建模竞赛B题)
图1 染色体、基因和位点的结构关系
表1 完全基因组数据库的样本采集结构图
| 样本编号 |
样本健康状况 |
染色体片段位点名称和位点等位基因信息 |
|||
| rs100015 |
rs56341 |
... |
rs21132 |
||
| 1 |
1 |
TT |
CA |
... |
GT |
| 2 |
0 |
TT |
CC |
... |
GG |
| 3 |
1 |
TC |
CC |
... |
GG |
| 4 |
1 |
TC |
CA |
... |
GG |
| 5 |
0 |
CC |
CC |
... |
GG |
| 6 |
0 |
TT |
CC |
... |
GG |
2 数据模型
数据集(gene_pheno_dataset)大小:27.1 MB
包含文件:
| 文件名称 |
数据描述 |
| genotype.dat |
样本在某条染色体片段上所有的位点信息 |
| phenotype.txt |
样本具有遗传疾病A的标签信息 |
数据清洗及分类提取后的数据集如下:
| 文件名称 |
数据描述 |
| genotype.dat |
替换缺失值后的样本位点的碱基对编码矩阵 |
| feature_name.txt |
所有位点属性的名称 |
| phenotype.txt |
样本具有遗传疾病A的标签信息 |
| nowenary_encoding_feature.dat |
样本位点特征属性的十进制编码矩阵 |
这里使用了位点测试数据集,来自1000个可能致病的染色体片段试验检测结果,标签分布为500个无病染色体使用0表示,500个患病染色体使用1表示,且每个致病染色体上有9445个碱基对,以此作为位点。采用十进制{0,1,2,3...}编码将每个碱基对转化成数据编码方式,以便于数据分析。“AA”为“0”;“AC”为“1”;“AG”为2;“AT”为3...“TT”为9,详见碱基对编码表2(其中{AC,CA};{CG,GC};...碱基对表示方式相同)。
表2 碱基对编码
| 碱基 |
A |
C |
G |
T |
| A |
0 |
1 |
3 |
6 |
| C |
1 |
2 |
4 |
7 |
| G |
3 |
4 |
5 |
8 |
| T |
6 |
7 |
8 |
9 |
另外,位点中出现字符‘I’和‘D’,根据说明,分别用‘T’和‘C’代替。
由于所有样本序列上的本一个二核苷酸位点代表了一个属性,本文总共有9445个位点即9445个不同的属性,这些属性由十进制表示(见图2)。其中,属性列中PC1~PCn表示9445个不同的属性指标;AA,AC,AG,AT,...,TT表示16中不同的原始二核苷酸。
图2 碱基对的十进制编码过程
3 算法设计原理与实现
本文要解决的是寻找遗传疾病A的致病基因位点,通过之前的分析,也就是对9445个位点属性进行分类预测,一类是致病基因位点(标签为label=1),另一类是非致病基因位点(标签为label=0),因而这个问题就转化为一个分类预测问题了。
算法设计上,我们分为两大块,包括:主函数(main.m)设计、预测函数(predictFunc_svm.m)设计。
3.1 主函数设计模块
基于本文要解决的问题,算法主函数要得到的结果应包括:9445个位点属性的预测精度(输出predict_accuracy.txt)、预测精度的降序排列结果及对应的位点序号(输出predict_accuracy_desc.txt)、Top n 预测精度及对应预测精度所在的位点名称(n取10)。
主函数算法实现步骤:
| 1) 开始; 2) 加载十进制编码9445个位点的所有属性数据all_feature(i,j); 3) 数据属性归一化处理,将十进制数据变换到(0, 1)区间上; 4) 循环每个位点,调用预测函数对每列属性进行该疾病的预测,得到预测精度accuracy; 5) 对预测结果降序排列,即预测精度 accuracy 从高到低排列; 6) 选出Top n 预测精度及对应预测精度所在的位点; 7) 结束。 |
其中,数据归一化处理过程中,对于第i个样本的第j个位点编码all_feature(i,j)做如下变换得到归一化的属性编码数据:
3.2 预测函数设计模块
本文采用K折交叉验证的实验测试方法及支持向量机(SVM)分类器来构造位点属性的分类预测函数,用于获取预测精度。在设计预测函数之前,先对K折交叉验证及支持向量机(SVM)的基本原理做出简单的介绍。
3.2.1 K折交叉验证
在机器学习中,为了得到可靠稳定的模型,往往会采取一些验证方法来进行测试,常用的精度测试方法主要是K折交叉验证(k-fold cross-validation)。其原理[1]为:将数据集A分为训练集(training-set)B和测试集(test-set)C,在样本量不充足的情况下,为了充分利用数据集对算法效果进行测试,将数据集A随机分为k个包,每次将其中一个包作为测试集,剩下k-1个包作为训练集进行训练。
在matlab中,可以利用:indices=crossvalind('Kfold',x,k);
来实现随机分包的操作,其中x为一个N维列向量(N为数据集A的元素个数,与x具体内容无关,只需要能够表示数据集的规模),k为要分成的包的总个数,输出的结果indices是一个N维列向量,每个元素对应的值为该单元所属的包的编号(即该列向量中元素是1~k的整随机数),利用这个向量即可通过循环控制来对数据集进行划分。例:
[M,N]=size(data);%数据集为一个M*N的矩阵,其中每一行代表一个样本
indices=crossvalind('Kfold',data(1:M,N),k);%进行随机分包
fork=1:k%交叉验证,k个包轮流作为测试集
test= (indices == k);%获得test集元素在数据集中对应的单元编号
train = ~test;%train集元素的编号为非test元素的编号
train_data=data(train,:);%从数据集中划分出train样本的数据
train_target=target(:,train);%获得样本集的测试目标
test_data=data(test,:);%test样本集
test_target=target(:,test);
3.2.2 支持向量机
支持向量机(supportvector machine,SVM)是机器学习里的一种分类算法,通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,即支持向量机的学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。具体原理[2]如下:
在n维空间中找到一个分类超平面,将空间上的点分类。如图3是线性分类的例子。
图3 线性分类示例图
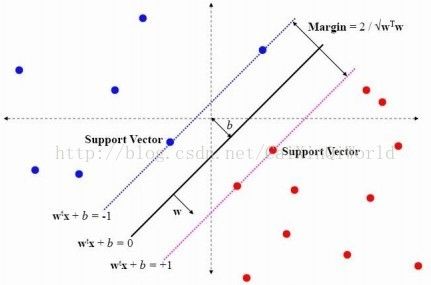
一般而言,一个点距离超平面的远近可以表示为分类预测的确信或准确程度。SVM就是要最大化这个间隔值Gap。而在虚线上的点便叫做支持向量Support Vector。
图4 支持向量机在低维空间下的线性分类原理图
实际中,我们会经常遇到线性不可分的情况,此时,我们的常用做法是把样本特征映射到高维空间中去(如图5)。线性不可分映射到高维空间,可能会导致维度大小高到可怕(19维乃至无穷维的例子),导致计算复杂。核函数的价值在于它虽然也是将特征进行从低维到高维的转换,但核函数绝就绝在它事先在低维上进行计算,而将实质上的分类效果表现在了高维上,也就如上文所说的避免了直接在高维空间中的复杂计算。
图5 支持向量机在高维空间下的非线性可分原理图
实际运用中,SVM用到了svmtrain和svmpredict两个主要函数:
(1) model=svmtrain(train_label, train_matrix, ['libsvm_options']);
其中:
train_label 表示训练集的标签;
train_matrix 表示训练集的属性矩阵;
libsvm_options 是需要设置的一系列参数,参见《libsvm 参数说明.txt》;
model 是训练得到的模型,是一个结构体。
(2) [predicted_label,accuracy/mse, decision_values]=svmpredict(test_label, test_matrix, model,['libsvm_options']);
其中:
test_label 表示测试集的标签;
test_matrix 表示测试集的属性矩阵;
model 是上面训练得到的模型;
libsvm_options 是需要设置的一系列参数;
predicted_label 表示预测得到的标签;
accuracy/mse 是一个3*1的列向量,其中第1个数字用于分类问题,表示分类准确率;后两个数字用于回归问题,第2个数字表示mse;第三个数字表示平方相关系数。
预测函数算法实现步骤:
| 1) 输入正类数据(Pdata)、负类数据(Ndata)和位点属性矩阵,输出原始预测精度Acc; 2) 构造5折交叉验证的正、负指数; 3) 进行K折交叉验证(K=5)(采用循环结构); 循环体的构建: 3.1) 选出数据集训练属性和测试属性; 3.2) 选出训练集和测试集中的正、负样本; 3.3) 训练集的标签和测试集的标签; 3.4) 通过SVM构建的预测器,训练集训练模型; 3.5) 通过SVM构建的预测器,测试集预测精度; 3.6) 取出分类预测精度结果; 4) 5折交叉计算累积得到一个1*5的预测精度矩阵,即Acc; 5) 输出结果。 |
4 代码架构与实现环境
基于以上算法设计与实现步骤,本项目各部分功能实现的代码架构如下:
本项目的程序实现环境如下:
| 主机系统 |
Windows 10 (64位) |
| 运行平台 |
Matlab R2011b (64位) |
| SVM工具箱 |
libsvm-3.12 |
本项目的程序运行结束文件如下:
| main.m |
主函数 |
| predictFunc_svm.m |
预测函数 |
| nowenary_encoding_feature.dat |
特征属性的十进制编码数据源 |
| gene_pheno_dataset |
原始数据集 |
| feature_name.txt |
特征属性(即:位点)的名称 |
| phenotype.txt |
构造分类器类别数据源 |
| predict_accuracy.txt |
预测精度结果 |
| predict_accuracy_desc.txt |
降序重排的预测精度结果 |
5 实验结果
取每列属性作为构建的预测器的输入,从而得到9445个位点中,每个位点利用该模型预测该疾病的预测精度accuracy。
图6 位点属性的预测精度折线趋势图及对应的统计分布盒图
如图6所示,对所得的预测精度按属性序号作出折线趋势图以及对应的统计分布盒图,容易看出预测精度整体分布在50%左右,且有一个明显的奇异值,也即与该疾病最相关的位点预测精度值。
致病位点的选择结果:
通过SVM分别预测得到降序排列的预测结果,选出前n个预测精度并得到对应的致病位点,本文n的取值为10,预测的结果如表2所示:
表3 致病位点的选择结果
| 序号 |
位点名称 |
Acc(%) |
| 1 |
'rs2273298' |
58.3000 |
| 2 |
'rs7543405' |
56.5000 |
| 3 |
'rs4391636' |
55.7000 |
| 4 |
'rs7368252' |
55.6000 |
| 5 |
'rs4646092' |
55.6000 |
| 6 |
'rs12145450' |
55.5000 |
| 7 |
'rs932372' |
55.4000 |
| 8 |
'rs2807345' |
55.2000 |
| 9 |
'rs9659647' |
55.2000 |
| 10 |
'rs12036216' |
55.0000 |
从表3的数据发现,利用支持向量机分类预测模型得出与该疾病相关性较高的致病基因有10个,它们分别为rs2273298、 rs7543405、rs4391636、rs7368252、rs4646092、rs12145450、rs932372、rs2807345、rs9659647、rs12036216,其中位点rs2273298对疾病A的致病性最强。
参考文献:
[1] cancanw. k-折交叉验证(k-fold crossValidation). http://www.cnblogs.com/wangccc/p/5307927.html.
[2] July.支持向量机通俗导论(理解SVM的三层境界). http://blog.csdn.net/v_july_v/article/details/7624837.