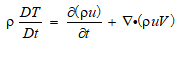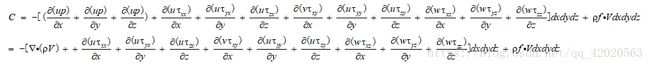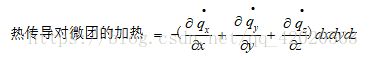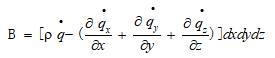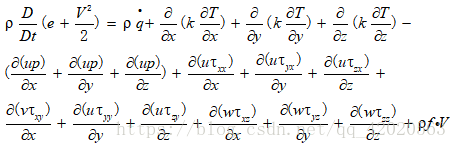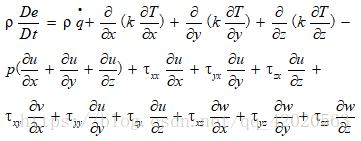【转】流体动力学控制方程（详细推导）

【转】流体动力学控制方程（详细推导） diyhoos

原文链接：https://blog.csdn.net/qq_42020563/article/details/80940387

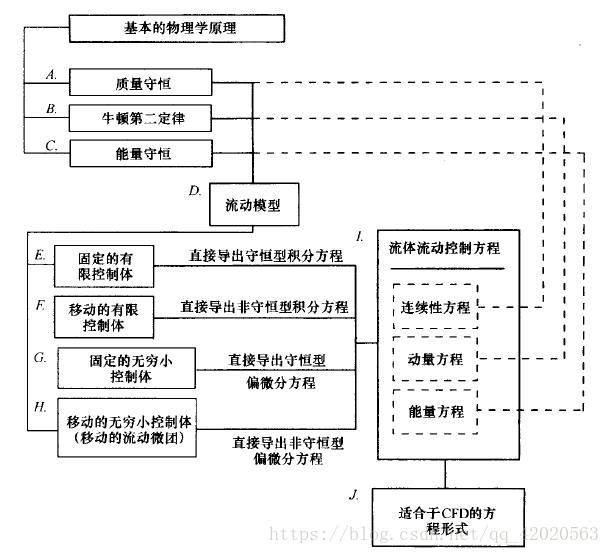
CFD建立在流体力学基本控制方程：连续性方程、动量方程、能量方程的基础上。这些方程式任何流动都必须遵守的3个基本物理学原理。这三个方程是这些原理的数学描述：

1. 质量守恒定律。
2. 牛顿第二定律。
3. 能量守恒定律。

      全部CFD都是基于这些方程的，在开展研究之前必须熟悉这些方程。如果不能从物理上理解每一个方程的意义，又怎么指望对数值求解这些方程所得到的结果做出正确的解读呢？接下来就来推导和讨论这些方程。

一、连续性方程

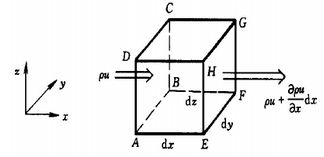
用一个微六面体元控制体建立微分形式的连续性方程。

设在流场中取一固定不动的微平行六面体（控制体），在直角坐标系oxyz中，六面体的边长取为dx，dy，dz。

先看x轴方向的流动，流体从ABCD面流入六面体，从EFGH面流出。

在x轴方向流出与流入质量之差

用同样的方法，在y轴和z轴方向上的质量之差为：

这样，在dt时间内通过六面体的全部六个面净流出的质量为：

在dt时间内，六面体的质量减少了

根据质量守恒定律，净流出六面体的质量必等于六面体内所减少的质量，则：

这就是直角坐标系中流体运动的微分形式的连续性方程

利用散度公式：

得到：

有的文献中用▽表示散度，因此上面式子又可表示为：

上面是连续性方程的偏微分方程形式，它是基于空间位置固定的无穷小微团模型。

二、动量守恒方程

动量守恒定律是任何流动系统都必须满足的定律。

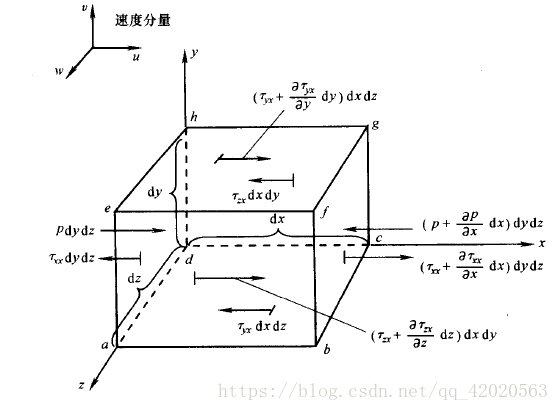
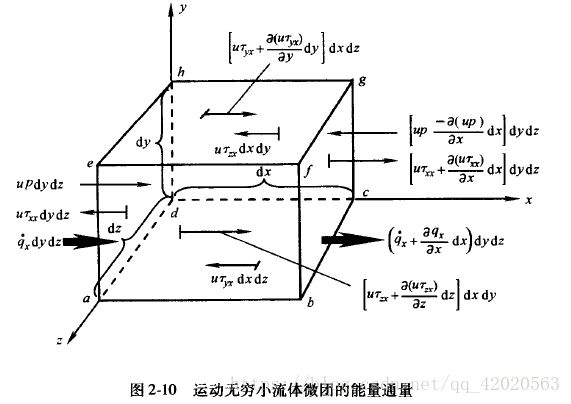
对上图一个运动流体微团进行分析，就是作用在微团上力的总和等于微团的质量乘以微团的加速度。这是一个向量关系式，我们将其沿x，y，z轴分解成三个标量的关系式。仅考虑其中x方向分量。

流体微团在x方向上受到两种力的作用：体积力和表面力。

• 体积力：直接作用在流体微团整个体积微团上的力，而且作用是超距离的，比如重力、电场力、磁场力
• 表面力：直接作用在流体微团的表面。由两种原因引起：1.由包在流体微团周围的流体所施加的，作用于微团表面的压力分布；2.由于外部流体推拉微团而产生的，以摩擦的方式作用于表面的切应力和正应力分布。

将作用在单位质量流体微团上的体积力记作f，其x方向分量为fx。流体微团的体积为dxdydz，所以：

将以上两式相加得到x方向总的力F，得到：

接下来考虑的右边，因为运动的流体微团其质量是固定不变的：

另外，流体微团的加速度就是速度变化的时间变化率，所以加速度得x方向分量，记作ax，直接就等于u的时间变化率，根据物质导数

则粘性流x方向的动量方程为：

同时，根据数学代换可知：

代入可得：

 

这就是纳维-斯托克斯方程的守恒形式（Navier-Stokes方程）

----------------------------------------------------------------------------------------------------------------------------------

注：

物质导数D/Dt，在物理上时跟踪一个运动的流体微团的时间变化率，第一项是当地导数，它在物理上是固定点处的时间变化率；后一项是迁移导数，在物理上表示由于流体微团从流场中的一点运动到另一点，流场的空间不均匀而引起的时间变化率。物质导数可用于任何流场变量，如ρ、T等

---------------------------------------------------------------------------------------------------------------------------------

三、能量方程

能量守恒定律是包含热交换系统必须满足的基本定律。该定律可表述为

微元体中能量的变化率=进入微元体的净热流量+体积力与表面力对微元体所做的功率

或：A=B+C

先计算C，作用在一个运动物体上的力，对物体做功的功率等于这个力乘以速度在运动方向上的分量，所以作用于速度V的流体微团上的体积力，做功的功率为：

表面力做功的功率为（仅考虑x方向上的表面力）：

同样可以类推出y、z方向上的表面力。则C等于

接下来看B，即进入微团内的总热流量。有来自体积加热，如吸收或释放的辐射热；由温度梯度导致的跨过表面的热输送，即热传导。定义q为单位质量的体积加热率，可得到：

将两项加和：

根据傅里叶热传导定律，热传导产生的热流与当地的温度梯度成正比

k为热导率

接下来研究A，运动流体微团的能量，有两个来源：

1. 由于分子随机运动产生的（单位质量）内能e
2. 流体微团平动时具有的动能，单位质量的动能为V^2/2

因此，单位质量的总能量变化的时间变化率由物质导数给出：

则能量方程为：

将方程改写只用e的形式：

该方程左边只包含内能的物质导数，动能的物质导数和右边的体积力已经去掉。

四、小结

       到目前为止，已经推导出了全部的流体控制方程，熟悉并理解它们的物理意义是绝对必要的。这也是我亲自打出这篇文章的目的所在。

--------------------- 作者：diyhoos 来源：CSDN 原文：https://blog.csdn.net/qq_42020563/article/details/80940387?utm_source=copy 版权声明：本文为博主原创文章，转载请附上博文链接！