思路来源
https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fr=aladdin
https://blog.csdn.net/duanruibupt/article/details/6869431
https://www.cnblogs.com/COLIN-LIGHTNING/p/8450053.html
https://blog.csdn.net/qq_36523667/article/details/78590002
https://blog.csdn.net/doc_sgl/article/details/8880468
卡特兰数通项公式
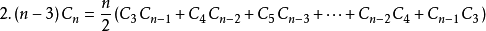
卡特兰数递推公式
令h(0)=1,h(1)=1，
catalan数满足递推式：
h(n)= h(0)*h(n-1)+h(1)*h(n-2) + ... + h(n-1)*h(0) (n>=2)
另类递推式：
h(n)=h(n-1)*(4*n-2)/(n+1);（可用于大数 求递推式）
递推关系的解为：
h(n)=C(2n,n)/(n+1) (n=0,1,2,...)
递推关系的另类解为：
h(n)=c(2n,n)-c(2n,n-1)(n=0,1,2,...)
卡特兰数的应用
①n个+1和n个-1构成2n项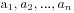
，其部分和满足
的序列个数等于第n个Catalan数
。
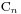证明：
假设不满足条件的序列个数为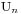
，那么就有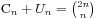
。
我们假设有一个最小的k令
。
由于这里k是最小的，所以必有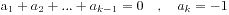
，并且k是一个奇数。
此时我们将前k项中的+1变为-1，将-1变为+1,那么就得到一个有(n+1)个+1和(n-1)个-1的序列了。
这样的序列个数就是我们要求的。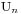
显然，Un分为两部分，
先出现-1的序列，其前缀和小于0，将序列最末一个+1改为-1即符合题意；
先出现+1的序列，按上述原则翻转回去，则符合原题意。
故只需在2n个数里任取(n+1)个数为1即可，数值大小为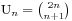 
。
那么我们就得到了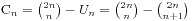
，就是我们前面的公式。
②若将+1改为左括号，-1改为右括号，则原问题变为括号的匹配问题。
括号的合法序列是指，对于任意的前缀，左括号数都不少于右括号数，显然是一个卡特兰数。
证明：
（1）空串是合法序列
（2）若A是合法序列且B是合法序列，则AB是合法序列
（3）若S为合法序列，且a为长度为k的左括号，b为长度为k的右括号，则aSb是合法序列
规定A是一个合法序列，B也是一个合法序列。
那么对于n对的括号序列，一定是A(B)的形式构成。
这里我们分别讨论假设，
B有0对括号，则A有(n-1)对；
B有1对……，
……
B有(n-1)对，则A有0对。
故f(n)=f(0)f(n-1)+…+f(n-1)f(0)，
根据卡特兰数的定义，显然是卡特兰数Cn。
③n个节点的二叉树的所有可能形态数为。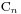
我们考虑随便取一个节点作为根，那么他左边和右边的儿子节点个数就确定了。
假定根节点标号为x，
那么左子树的标号就从1到x-1,共x-1个，右子树的标号就从x+1到n，共n-x个。
那么我们的x从1取到n，就获得了所有的情况数
。
④求解路径方案数：
对于一个n*n的正方形网格，每次我们能向右或者向上移动一格，
那么从左下角到右上角的所有在副对角线右下方的路径总数为。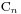
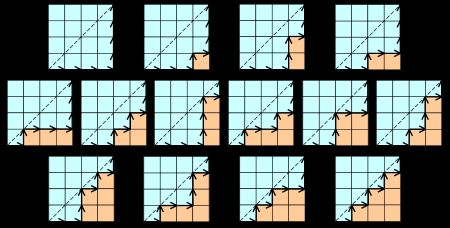
我们将一条水平边记为+1,垂直边记为-1,那么就组成了一个n个+1和n个-1的序列，
我们所要保证的就是前k步中水平边的个数不小于垂直边的个数，
换句话说前k个元素的和非负，即卡特兰数定义。
⑤求01串的个数：
n个0与n个1构成的序列方案数，使得任何一个前缀0的个数不少于1的个数。
显然把0改为左括号，1改为右括号就变成了合法括号序列匹配问题。
⑥求凸边形进行三角剖分的不同方案数：
在一个有n+3条边的凸多边形中，求通过若干条互不相交的对角线，把这个多边形划分成若干个三角形的不同方案数。
因为每一条边都一定是剖分后的三角形的一条边，
任意一条边都会把多边形分成两个小多边形，
那么根据乘法原理，解即为划分成不同多边形的方案数对应小多边形的划分方案数之和。
⑦求出栈方案数：
我们会把n个数分成两部分来处理。
就是必须等第一部分全部排空后，第二部分的数才能入栈。
两部分分别对应一个方案数，互不相干，线性求积。
1和n-1是独立的两部分。公式就是f(1)*f(n-1)，
如果2和n-2是独立的两部分。公式就是f(2)*f(n-2)，
以此类推，就最终可以推到f(n-1)*f(1)，
线性相加，即卡特兰数。
总结
方案数是卡特兰数的特征，
①可以以某位置为划分，将原情况划分为两个更小的子情况。
②类似前缀和非负的操作，如左括号数不少于右括号数等。
代码实现（大数 卡特兰数）
#include
#include
#include
#include
#include
#include
#include
#include
