Code92007
Code92007

CCPC-Wannafly Winter Camp Day5 E.Fast Kronecker Transform(离散化+NTT)

题目

思路来源

dls

题解

先离散化，把a和b搞进一个序列，然后排序去重，把a和b赋为rank值

然后遍历这个不重复的序列，两个大于1W就建2e5数列用NTT搞，否则直接暴力

 

既然要在ai和bj值相同，下标i+j==k时求i*j的值，

那么就把位置i和j分别放入值的vector里，对相同值的vector进行NTT

注意多项式乘法一定会遍历所有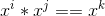x^{i}*x^{j}==x^{k}的情形，所以就令f(x)的第i位为i，g(x)的第j位为j

是一种很自然的做法，注意多项式乘法的定义

 

这个1W卡的真是刚刚好啊……昨天T了若干发

注意 NTT里面取模不要判if 直接模

上面的是有if的 下面的是没if的

NTT和FFT类似，处理整数取模的情况，

可以把大素数搞成它的原根，998244353的原根是3

FFT卡精度过不了

代码

#include 
#include  
#include 
#include 
#include 
#include 
#include  
#define g 3
using namespace std;
typedef long long ll;
const double PI = acos(-1.0);
const int mod=998244353;
const int maxn=1e5+10;
const int G=3;
ll inv,N;
ll n,m,tmp1[maxn*3],tmp2[maxn*3],rev[maxn*3],back[maxn*3];
vectorq[maxn*2],p[maxn*2];
vectornum;
ll a[maxn],b[maxn],c[maxn*2];
ll power(ll x,ll y)
{
    ll res=1ll;
    for(;y;y>>=1)
    {
        if(y&1)res=res*x%mod;
        x=x*x%mod;
    }
    return res;
}
void init()
{
    int len=0;
    while((n+m+2)>=(1<>=1;
        }
        back[i]=rev[i]=pos;
    }
}
void init2()
{
	for(int i=0;ii)
        {
            swap(a[i],a[rev[i]]);
        }
    }
    for(int i=2;i<=n;i<<=1)
    {
        ll mid=i>>1;
        ll wn=power(G,(mod-1)/i);
        if(re) wn=power(wn,(mod-2));
        for(int j=0;j

你可能感兴趣的:(FFT/NTT/FWT/FMT)

  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • 遥感影像的切片处理 sand&wich 计算机视觉python图像处理
    在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
  • 20个新手学习c++必会的程序 输出*三角形、杨辉三角等（附代码） X_StarX c++学习算法大学生开发语言数据结构
    示例1:HelloWorld#includeusingnamespacestd;intmain(){coutusingnamespacestd;intmain(){inta=5;intb=10;intsum=a+b;coutusingnamespacestd;intfactorial(intn){if(nusingnamespacestd;voidprintFibonacci(intn){intt
  • 使用由 Python 编写的 lxml 实现高性能 XML 解析 hunyxv python笔记pythonxml
    转载自：文章lxml简介Python从来不出现XML库短缺的情况。从2.0版本开始，它就附带了xml.dom.minidom和相关的pulldom以及SimpleAPIforXML(SAX)模块。从2.4开始，它附带了流行的ElementTreeAPI。此外，很多第三方库可以提供更高级别的或更具有python风格的接口。尽管任何XML库都足够处理简单的DocumentObjectModel(DOM
  • Go语言基础总结 Alice_小哪吒 Go学习笔记golang开发语言后端
    一、Go语言结构包声明引入包函数变量语句&表达式注释下面简单给出hello.go文件。packagesrc/*定义包名*/import"fmt"/*引入包*/funchello(){/*函数*/fmt.Println("Hello,World!")/*语句&表达式*/fmt.Println("菜鸟教程：runoob.com")}二、Go语言基础语法Go程序可以由多个标记构成。可以是关键字、标识符、
  • golang 实现文件上传下载 wangwei830 go
    Gin框架上传下载上传（支持批量上传）httpRouter.POST("/upload",func(ctx*gin.Context){forms,err:=ctx.MultipartForm()iferr!=nil{fmt.Println("error",err)}files:=forms.File["fileName"]for_,v:=rangefiles{iferr:=ctx.SaveUplo
  • golang实现从服务器下载文件到本地指定目录 余生逆风飞翔 golang服务器开发语言
    一、连接服务器，采用sftp连接模式packagemiddlewaresimport("fmt""time""github.com/pkg/sftp""golang.org/x/crypto/ssh")//建立服务器连接funcConnect(user,password,hoststring,portint)(*sftp.Client,error){var(auth[]ssh.AuthMethod
  • 2021-06-07 Do What You Are Meant To Do 春生阁
    Don’tgiveupontryingtofindbalanceinyourlife.Sticktoyourpriorities.Rememberwhat’smostimportanttoyouanddoeverythingyoucantoputyourselfinapositionwhereyoucanfocusonthosepriorities,ratherthanbeingpulledbyt
  • ffmpeg批量将tif文件转成jpeg格式 winfredzhang 图像工具ffmpegtifjpeg转换
    1、cmd2、切换到安装ffmpeg的路径。3、输入命令：ffmpeg-start_number001-i"D:\ocr\%03d.tif"-start_number001-pix_fmtyuv420p-qscale:v1"D:\ocr\%03d.jpg"结果。
  • Go 语言基本架构 Fe_cow丿 Go
    Go基本架构一、Go基本架构：packagemainimport"fmt"funcmain(){fmt.Println("hello,world")}go文件的后缀是.go；packagemain：表示文件所在的包是main；每个Go应用程序都包含一个为main的包；所有包名都应该使用小写字母；import“fmt”：表示引入一个包，包名为fmt，引入该包后，就可以使用fmt包的函数；比如：fmt
  • 2019-03-31 梨筱草
    图片发自AppIfyouwanttochangesomething,startwithbabysteps.Takeasmallaction-anyaction-andgrowfromthere.如果你想要做出改变，就从第一步开始。做出一点小的行动，任何一种行动都行，然后就从这里开始。Ifyouwanttochangesomething,startwithbabysteps.Takeasmallac
  • P1576 最小花费 「已注销」 算法c++数据结构
    ![](最小花费-洛谷)#includeusingnamespacestd;inthead[200010],tim;doubledis[200010];boolflag[200010];structcsz{intto;doublew;intnext;}edge[200010];voidadd(intu,intv,doublew){edge[++tim].to=v;edge[tim].w=1.0-w
  • SpringBoot 设置传入参数非必要 loveLifeLoveCoding springbootspringbootjavaspring
    查看RequestParam源码packageorg.springframework.web.bind.annotation;importjava.lang.annotation.Documented;importjava.lang.annotation.ElementType;importjava.lang.annotation.Retention;importjava.lang.annotat
  • HTTP 请求处理的完整流程到Servlet流程图 烟雨国度 httpservlet流程图
    HTTP请求处理的完整流程。从TCP三次握手开始，一直到Servlet处理请求并返回响应。首先，让我解释一下response.setContentType("text/html;charset=UTF-8");这行代码：这行代码设置了HTTP响应的Content-Type头。它告诉浏览器：响应的内容类型是HTML(text/html)字符编码是UTF-8(charset=UTF-8)这样浏览器就知
  • P2865 [USACO06NOV] Roadblocks G（洛谷）(次短路) 叶子清不青 算法
    开一个二维数组dis[N][2]分别记录最短路和次短路即可。dijkstra和spfa均可，推荐spfa。//dijkstra#includeusingnamespacestd;constintN=1e5+5;typedeflonglongll;typedefpairPII;intn,m,k;intT;priority_queue,greater>q;structnode{inte,w;};vec
  • Jacoco的XML报告详解 CrissChan 自动化测试持续交付和持续测试jacoco测试
    使用jacococli完成jacoco测试报告生成后，会看到有一个.xml结尾的文件，这个就是xml格式的覆盖率报告。除了xml还有csv、html格式的报告，本文进介绍xml报告。DTD文件在介绍jacoco的xml报告之前，我们应该先看一下对应的DTD文件的内容。(DTD的全称为DocumentTypeDefinition，是一种文件定义格式，它规定了XML文件结构为XML文件提供了语法与规则
  • golang面试题 001 Jay_hj11 golang面试Golanggolang后端数据结构开发语言面试
    001gochannelclose后读的问题golangchannel关闭后，其中剩余的数据，是可以继续读取的。请看下面的测试例子。创建一个带有缓冲的channel，向channel中发送数据，然后关闭channel，最后，从channel中读取数据，输出结果。packagemainimport"fmt"//gochannelclose后读的问题funcmain(){ch:=make(chanst
  • C++ | Leetcode C++题解之第398题随机数索引 Ddddddd_158 经验分享C++Leetcode题解
    题目：题解：classSolution{vector&nums;public:Solution(vector&nums):nums(nums){}intpick(inttarget){intans;for(inti=0,cnt=0;i
  • 面试经典 150 题 2 —（二分查找）— 74. 搜索二维矩阵 BreezeChasingDrizzle leetcode矩阵算法leetcodec++二分查找
    74.搜索二维矩阵方法classSolution{public:boolsearchMatrix(vector>&matrix,inttarget){intmatrixRows=matrix.size(),matrixCols=matrix[0].size();//先找target所在的行inttargetAtRow=-1;for(inti=0;i>&matrix,inttarget){intma
  • 【C++】日期和时间 守月满空山雪照窗 Codec++
    C++提供了多种处理日期和时间的功能，主要通过标准库和提供。以下是C++中处理日期和时间的功能介绍及其用法：1.库是C++中处理时间的传统库，提供了一些基本的时间操作函数。这些函数主要基于C语言的时间处理方式，适合处理简单的时间任务。1.1.获取当前时间#include#includeintmain(){//获取当前时间std::time_tcurrentTime=std::time(nullpt
  • golang文件相对路径问题 jzpfbpx golang开发语言后端
    目录结构2.具体代码：constdataFile="../data/data.json"_,fileName,_,_:=runtime.Caller(1)dataPath:=path.Join(path.Dir(fileName),dataFile)fmt.Println(dataPath)//openfilefile,err:=os.Open(dataPath)iferr!=nil{log.Fa
  • golang文件相对路径问题 jzpfbpx golang开发语言后端
    1.目录结构2.具体代码：constdataFile="../data/data.json"_,fileName,_,_:=runtime.Caller(1)dataPath:=path.Join(path.Dir(fileName),dataFile)fmt.Println(dataPath)//openfilefile,err:=os.Open(dataPath)iferr!=nil{log.
  • 甘特图组件DHTMLX Gantt中文教程 - 如何实现持久UI状态 界面开发小八哥 甘特图uiDHTMLX项目管理javascript
    DHTMLXGantt是用于跨浏览器和跨平台应用程序的功能齐全的Gantt图表。可满足项目管理应用程序的所有需求，是最完善的甘特图图表库。在现代Web应用程序中，在页面重新加载之间保持UI元素的状态对于流畅的用户体验至关重要。在本教程中我们将知道您完成DHTMLXGantt中持久UI的简单实现，重点关注一小部分特性——即任务的展开或折叠分支，以及选定的甘特图缩放级别。您将了解如何将这些设置存储在浏
  • Linux从入门到开发实战(C/C++)Day09-poll和epoll 黒井深 c语言c++linux
    poll：和select差不多#includeintpoll(structpollfd*fds,nfds_tnfds,inttimeout);与select共同点：还是轮询（轮询结构体数组）区别1：监视的不是描述符号集合，是结构体数组structpollfd{intfd;/*filedescriptor*/shortevents;/*requestedevents需要监视的事件*/shortrev
  • Unity3d俯视视角下，通过点击屏幕获取世界坐标是如何实现的 睡不醒的小泽 Unityunity
    方式一：射线转化在Unity3D中，我们先获取对应游戏画面的摄像机，之后获取屏幕点击位置的世界坐标可以通过使用ScreenPointToRay()函数实现。这个函数将屏幕坐标（在屏幕上的位置，范围从0到屏幕宽度和高度）转换为世界坐标（在世界空间中的位置）。这种方法在rts类游戏和一些3d项目的RPG游戏中比较常见。实现的方法可以概括为：根据Input.mousePosition，从camera射出
  • c语言宏不能传递参数,C语言 如何在宏定义中使用可变参数 左右不对称定律 c语言宏不能传递参数
    有一个记录日志的函数,想用宏定义进行包装，简化调用方法，但是xlc报如下的错误：void_log(constintlevel,char*file,intline,constchar*fmt,...){va_listap;intcount;time_tt;structtm*st;charstr_time[255];memset(str_time,0x00,sizeof(str_time));time
  • 网络套接字编程（二） knight-n 网络网络linuxc++
    socket常见API创建套接字：（TCP/UDP，客户端+服务器）intsocket(intdomain,inttype,intprotocol);绑定端口号：（TCP/UDP，服务器）intbind(intsockfd,conststructsockaddr*addr,socklen_taddrlen);监听套接字：（TCP，服务器）intlisten(intsockfd,intbacklog
  • C# 网口通信（通过Sockets类） 萨达大 c#服务器网络网口通讯上位机
    文章目录1.引入Sockets2.定义TcpClient3.连接网口4.发送数据5.关闭连接1.引入SocketsusingSystem.Net.Sockets;2.定义TcpClientprivateTcpClienttcpClient;//TcpClient实例privateNetworkStreamstream;//网络流，用于与服务器通信3.连接网口tcpClient=newTcpClie
  • Online Conversion of a Non-Partitioned Table to a Partitioned Table in Oracle Database 12c Release 2 IT皮特 数据库oracle
    从12.2开始，通过MODIFYTABLE可以在线实现普通表转分区表。一、创建测试表：DROPTABLEt1PURGE;CREATETABLEt1(idNUMBER,descriptionVARCHAR2(50),created_dateDATE,CONSTRAINTt1_pkPRIMARYKEY(id));CREATEINDEXt1_created_date_idxONt1(created_da
  • 博弈论专题 kuangbin题单（巴什，威佐夫，nim，fib博弈）+SG函数打表 我不是手机 博弈论
    省赛前先练着，回来补完巴什博弈：一堆n个物品两个人来拿，每人至少拿一个，最多拿m个，问最后取完的人win判断条件：n%(m+1)!=0cin>>n>>m;if(n%(m+1)!=0)cout>a>>b;if(a>b)swap(a,b);inttemp=(b-a
  • 关于旗正规则引擎下载页面需要弹窗保存到本地目录的问题 何必如此 jsp超链接文件下载窗口
    生成下载页面是需要选择“录入提交页面”，生成之后默认的下载页面<a>标签超链接为：<a href="<%=root_stimage%>stimage/image.jsp?filename=<%=strfile234%>&attachname=<%=java.net.URLEncoder.encode(file234filesourc
  • 【Spark九十八】Standalone Cluster Mode下的资源调度源代码分析 bit1129 cluster
    在分析源代码之前，首先对Standalone Cluster Mode的资源调度有一个基本的认识： 首先，运行一个Application需要Driver进程和一组Executor进程。在Standalone Cluster Mode下，Driver和Executor都是在Master的监护下给Worker发消息创建(Driver进程和Executor进程都需要分配内存和CPU，这就需要Maste
  • linux上独立安装部署spark daizj linux安装spark1.4部署
    下面讲一下linux上安装spark，以 Standalone Mode 安装   1）首先安装JDK   下载JDK：jdk-7u79-linux-x64.tar.gz  ，版本是1.7以上都行，解压 tar -zxvf jdk-7u79-linux-x64.tar.gz     然后配置 ~/.bashrc&nb
  • Java 字节码之解析一 周凡杨 java字节码javap
        一： Java 字节代码的组织形式   类文件 {     OxCAFEBABE ，小版本号，大版本号，常量池大小，常量池数组，访问控制标记，当前类信息，父类信息，实现的接口个数，实现的接口信息数组，域个数，域信息数组，方法个数，方法信息数组，属性个数，属性信息数组 } &nbs
  • java各种小工具代码 g21121 java
    1.数组转换成List import java.util.Arrays; Arrays.asList(Object[] obj); 2.判断一个String型是否有值 import org.springframework.util.StringUtils; if (StringUtils.hasText(str)) 3.判断一个List是否有值 import org.spring
  • 加快FineReport报表设计的几个心得体会 老A不折腾 finereport
    一、从远程服务器大批量取数进行表样设计时，最好按“列顺序”取一个“空的SQL语句”，这样可提高设计速度。否则每次设计时模板均要从远程读取数据，速度相当慢！！ 二、找一个富文本编辑软件（如NOTEPAD+）编辑SQL语句，这样会很好地检查语法。有时候带参数较多检查语法复杂时，结合FineReport中生成的日志，再找一个第三方数据库访问软件（如PL/SQL）进行数据检索，可以很快定位语法错误。
  • mysql linux启动与停止 墙头上一根草
    如何启动/停止/重启MySQL一、启动方式1、使用 service 启动：service mysqld start2、使用 mysqld 脚本启动：/etc/inint.d/mysqld start3、使用 safe_mysqld 启动：safe_mysqld&二、停止1、使用 service 启动：service mysqld stop2、使用 mysqld 脚本启动：/etc/inin
  • Spring中事务管理浅谈 aijuans spring事务管理
    Spring中事务管理浅谈 By Tony Jiang@2012-1-20 Spring中对事务的声明式管理 拿一个XML举例 [html]  view plain copy print ? <?xml version="1.0" encoding="UTF-8"?>&nb
  • php中隐形字符65279（utf-8的BOM头）问题 alxw4616
    php中隐形字符65279（utf-8的BOM头）问题 今天遇到一个问题. php输出JSON 前端在解析时发生问题:parsererror.   调试: 1.仔细对比字符串发现字符串拼写正确.怀疑是 非打印字符的问题. 2.逐一将字符串还原为unicode编码. 发现在字符串头的位置出现了一个 65279的非打印字符.        
  • 调用对象是否需要传递对象(初学者一定要注意这个问题) 百合不是茶 对象的传递与调用技巧
        类和对象的简单的复习,在做项目的过程中有时候不知道怎样来调用类创建的对象,简单的几个类可以看清楚,一般在项目中创建十几个类往往就不知道怎么来看   为了以后能够看清楚,现在来回顾一下类和对象的创建,对象的调用和传递(前面写过一篇)   类和对象的基础概念:   JAVA中万事万物都是类 类有字段(属性),方法,嵌套类和嵌套接
  • JDK1.5 AtomicLong实例 bijian1013 javathreadjava多线程AtomicLong
    JDK1.5 AtomicLong实例 类 AtomicLong 可以用原子方式更新的 long 值。有关原子变量属性的描述，请参阅 java.util.concurrent.atomic 包规范。AtomicLong 可用在应用程序中（如以原子方式增加的序列号），并且不能用于替换 Long。但是，此类确实扩展了 Number，允许那些处理基于数字类的工具和实用工具进行统一访问。  
  • 自定义的RPC的Java实现 bijian1013 javarpc
            网上看到纯java实现的RPC，很不错。         RPC的全名Remote Process Call，即远程过程调用。使用RPC，可以像使用本地的程序一样使用远程服务器上的程序。下面是一个简单的RPC 调用实例，从中可以看到RPC如何
  • 【RPC框架Hessian一】Hessian RPC Hello World bit1129 Hello world
    什么是Hessian The Hessian binary web service protocol makes web services usable without requiring a large framework, and without learning yet another alphabet soup of protocols. Because it is a binary p
  • 【Spark九十五】Spark Shell操作Spark SQL bit1129 shell
    在Spark Shell上，通过创建HiveContext可以直接进行Hive操作   1. 操作Hive中已存在的表   [hadoop@hadoop bin]$ ./spark-shell Spark assembly has been built with Hive, including Datanucleus jars on classpath Welcom
  • F5　往header加入客户端的ip ronin47
    when HTTP_RESPONSE {if {[HTTP::is_redirect]}{         HTTP::header replace Location [string map {:port/ /} [HTTP::header value Location]]HTTP::header replace Lo
  • java-61-在数组中，数字减去它右边(注意是右边)的数字得到一个数对之差. 求所有数对之差的最大值。例如在数组{2, 4, 1, 16, 7, 5, bylijinnan java
    思路来自： http://zhedahht.blog.163.com/blog/static/2541117420116135376632/ 写了个java版的 public class GreatestLeftRightDiff { /** * Q61.在数组中，数字减去它右边(注意是右边)的数字得到一个数对之差。 * 求所有数对之差的最大值。例如在数组
  • mongoDB 索引 开窍的石头 mongoDB索引
    在这一节中我们讲讲在mongo中如何创建索引       得到当前查询的索引信息      db.user.find(_id:12).explain();        cursor: basicCoursor 指的是没有索引  &
  • [硬件和系统]迎峰度夏 comsci 系统
      从这几天的气温来看，今年夏天的高温天气可能会维持在一个比较长的时间内    所以，从现在开始准备渡过炎热的夏天。。。。    每间房屋要有一个落地电风扇，一个空调(空调的功率和房间的面积有密切的关系)    坐的，躺的地方要有凉垫，床上要有凉席       电脑的机箱
  • 基于ThinkPHP开发的公司官网 cuiyadll 行业系统
    后端基于ThinkPHP，前端基于jQuery和BootstrapCo.MZ 企业系统 轻量级企业网站管理系统 运行环境:PHP5.3+, MySQL5.0 系统预览 系统下载：http://www.tecmz.com 预览地址：http://co.tecmz.com 各种设备自适应 响应式的网站设计能够对用户产生友好度，并且对于
  • Transaction and redelivery in JMS (JMS的事务和失败消息重发机制) darrenzhu jms事务承认MQacknowledge
    JMS Message Delivery Reliability and Acknowledgement Patterns http://wso2.com/library/articles/2013/01/jms-message-delivery-reliability-acknowledgement-patterns/ Transaction and redelivery in
  • Centos添加硬盘完全教程 dcj3sjt126com linuxcentoshardware
    Linux的硬盘识别: sda        表示第1块SCSI硬盘 hda       表示第1块IDE硬盘 scd0      表示第1个USB光驱 一般使用“fdisk -l”命
  • yii2 restful web服务路由 dcj3sjt126com PHPyii2
    路由 随着资源和控制器类准备，您可以使用URL如 http://localhost/index.php?r=user/create访问资源，类似于你可以用正常的Web应用程序做法。 在实践中，你通常要用美观的URL并采取有优势的HTTP动词。 例如，请求POST /users意味着访问user/create动作。 这可以很容易地通过配置urlManager应用程序组件来完成 如下所示
  • MongoDB查询(4)——游标和分页[八] eksliang mongodbMongoDB游标MongoDB深分页
    转载请出自出处：http://eksliang.iteye.com/blog/2177567 一、游标         数据库使用游标返回find的执行结果。客户端对游标的实现通常能够对最终结果进行有效控制，从shell中定义一个游标非常简单，就是将查询结果分配给一个变量（用var声明的变量就是局部变量），便创建了一个游标，如下所示： > var
  • Activity的四种启动模式和onNewIntent() gundumw100 android
    Android中Activity启动模式详解 　　在Android中每个界面都是一个Activity，切换界面操作其实是多个不同Activity之间的实例化操作。在Android中Activity的启动模式决定了Activity的启动运行方式。 　　Android总Activity的启动模式分为四种： Activity启动模式设置： <acti
  • 攻城狮送女友的CSS3生日蛋糕 ini htmlWebhtml5csscss3
    在线预览：http://keleyi.com/keleyi/phtml/html5/29.htm   代码如下：   <!DOCTYPE html> <html> <head> <meta charset="UTF-8"> <title>攻城狮送女友的CSS3生日蛋糕-柯乐义<
  • 读源码学Servlet（1）GenericServlet 源码分析 jzinfo tomcatWebservlet网络应用网络协议
    Servlet API的核心就是javax.servlet.Servlet接口，所有的Servlet 类（抽象的或者自己写的）都必须实现这个接口。在Servlet接口中定义了5个方法，其中有3个方法是由Servlet 容器在Servlet的生命周期的不同阶段来调用的特定方法。     先看javax.servlet.servlet接口源码：  package
  • JAVA进阶：VO(DTO)与PO(DAO)之间的转换 snoopy7713 javaVOHibernatepo
      PO即 Persistence Object　　VO即 Value Object 　VO和PO的主要区别在于：　　VO是独立的Java Object。　　PO是由Hibernate纳入其实体容器（Entity Map）的对象，它代表了与数据库中某条记录对应的Hibernate实体，PO的变化在事务提交时将反应到实际数据库中。 　实际上，这个VO被用作Data Transfer
  • mongodb group by date 聚合查询日期 统计每天数据（信息量） qiaolevip 每天进步一点点学习永无止境mongodb纵观千象
    /* 1 */ { "_id" : ObjectId("557ac1e2153c43c320393d9d"), "msgType" : "text", "sendTime" : ISODate("2015-06-12T11:26:26.000Z")
  • java之18天 常用的类(一) Luob. MathDateSystemRuntimeRundom
    System类 import java.util.Properties; /** * System: * out:标准输出,默认是控制台 * in:标准输入,默认是键盘 * * 描述系统的一些信息 * 获取系统的属性信息:Properties getProperties(); * * * */ public class Sy
  • maven wuai maven
    1、安装maven：解压缩、添加M2_HOME、添加环境变量path 2、创建maven_home文件夹，创建项目mvn_ch01,在其下面建立src、pom.xml，在src下面简历main、test、main下面建立java文件夹 3、编写类，在java文件夹下面依照类的包逐层创建文件夹，将此类放入最后一级文件夹 4、进入mvn_ch01 4.1、mvn compile ,执行后会在
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他