(转载)快速沃尔什变换(FWT) (知识整理+板子总结)
思路来源
https://blog.csdn.net/john123741/article/details/76576925
https://www.cnblogs.com/cjyyb/p/9065615.html（含and、or、xor具体证明过程）
强力安利思路来源博主的博客，翻了好几个都看不懂，这两位比较清晰……
用途
，
a数组如果在第i位为1，b数组在第j位为1，
那么卷积c数组在对应第k位为1
在这里可以是集合的与(and)，或(or)，异或(xor)
概念
FWT与FFT思想类似，通过一种转换，
把向量A和B分别加密成和其等长的向量AA和BB，
加密后的向量可以直接执行向量一对一的乘法，
即(x1,y1,z1)*(x2,y2,z2)==(x1*x2,y1*y2,z1*z2)这种，拓展到高维，
然后得到向量CC(x1*x2,y1*y2,z1*z2)，CC再解密，即得向量C
由于要求C与向量A和向量B的卷积相等，所以如何构造加密方式是一种问题
这里用@表示卷积运算，+表示数字的加法运算，∗表示数字的乘法运算。
设A，B为一个长为
的向量，如果A,B不足，需要可以用0补齐，
设C=A@B，C也是一个的向量。
设tf(A)是对A做一次FWT的结果，结果也是一个的向量，
如果可以做FWT，需要满足的条件是：
tf(C)=tf(A)∗tf(B)，其中上面的*表示两个向量对应为相乘。
对于异或的运算来说
①当k=0，tf(A)=A
②当k>0时，tf(A)=(tf(A0)+tf(A1),tf(A0)−tf(A1))
其中A0表示向量A的前
维，A1表示向量A的后维，
tf(A0)+tf(A1)和tf(A0)−tf(A1)是一个的向量，
而(tf(A0)+tf(A1),tf(A0)−tf(A1))就表示把二者连接起来，
成为一个的向量，是一个递归分治的过程。
下证在异或条件下，有tf(C)=tf(A)∗tf(B)
（以下k，都是指向量长度为）
引理：tf(A+B)=tf(A)+tf(B)
证明：
①k=0时，tf(A+B)=A+B=tf(A)+tf(B)，成立
②k>0时，设k-1时成立，
则tf(A+B)=(tf(A0+B0)+tf(A1+B1),tf(A0+B0)−tf(A1+B1))
由A0+B0 和A1+B1长度为，
有tf(A0+B0)=tf(A0)+tf(B0)，tf(A1+B1)=tf(A1)+tf(B1)成立
故有，
tf(A+B)
=(tf(A0)+tf(B0)+tf(A1)+tf(B1),tf(A0)+tf(B0)−tf(A1)−tf(B1))
=(tf(A0)+tf(A1),tf(A0)−tf(A1))+(tf(B0)+tf(B1),tf(B0)−tf(B1))
=tf(A)+tf(B)，成立，
数学归纳法知引理tf(A+B)=tf(A)+tf(B)成立
下证tf(C)=tf(A)∗tf(B)成立
证明：
①当k=0时，tf(C)=C=A∗B=tf(A)∗tf(B)
②当k>0时，设k-1时成立，
由tf(A)=(tf(A0)+tf(A1),tf(A0)−tf(A1))，tf(B)=(tf(B0)+tf(B1),tf(B0)−tf(B1))
tf(A)∗tf(B)
=((tf(A0)+tf(A1))∗(tf(B0)+tf(B1)),(tf(A0)−tf(A1))∗(tf(B0)−tf(B1))（将括号展开）
=(tf(A0)∗tf(B0)+tf(A0)∗tf(B1)+tf(A1)∗tf(B0)+tf(A1)∗tf(B1),tf(A0)∗tf(B0)−tf(A0)∗tf(B1)−tf(A1)∗tf(B0)+tf(A1)∗tf(B1))
由tf(A0)∗tf(B0)长度为， 有tf(A0)∗tf(B0)=tf(A0@B0)
故原式=(tf(A0@B0)+tf(A1@B1)+tf(A0@B1)+tf(A1@B0)，tf(A0@B0)+tf(A1@B1)−tf(A0@B1)−tf(A1@B0))
由异或每位都是独立的，根据最高位是0还是1，把A和B分别拆成了两部分。
所以C=(C0,C1)=(A0∗B0+A1∗B1,A0∗B1+A1∗B0)
C0=A0∗B0+A1∗B1表示当A、B最高位同为0或同为1时，异或结果为0
同理，C1=A0∗B1+A1∗B0表示当A、B最高位有且仅有一个1时，异或结果为1
tf(C)=tf(C0,C1)
=tf(A0@B0+A1@B1,A0@B1+A1@B0)
=(tf(A0@B0+A1@B1)+tf(A0@B1+A1@B0),tf(A0@B0+A1@B1)−tf(A0@B1+A1∗B0))
=(tf(A0@B0)+tf(A1@B1)+tf(A0@B1)+tf(A1@B0),tf(A0@B0)+tf(A1@B1)−tf(A0@B1)−tf(A1@B0))
=(tf(A0)∗tf(B0)+tf(A0)∗tf(B1)+tf(A1)∗tf(B0)+tf(A1)∗tf(B1),tf(A0)∗tf(B0)−tf(A0)∗tf(B1)−tf(A1)∗tf(B0)+tf(A1)∗tf(B1))
=((tf(A0)+tf(A1))∗(tf(B0)+tf(B1)),(tf(A0)−tf(A1))∗(tf(B0)−tf(B1))
=tf(A)*tf(B)，得证
tf函数得证，其逆函数ntf证明与其类似，
麻麻我再也不想看证明了
下面不加证明地给出三种运算的tf函数和ntf函数：
异或（Xor）
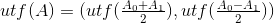
与（And）
或（Or）
板子1
//当⊕是^, &, |等某种位运算时，即是FWT快速沃尔什变换。
//FWT时，数组长度需要是2的整数次幂，不足补0。
//快速沃尔什变换
//防溢出可mod 1e9+7，则除以2的时候乘2的逆元。
//FWT后，相乘，UFWT回去即可
void FWT(int a[],int n)
{
for(int d=1;d板子2（来自yyb巨神的博客园，长得更像FFT）
//inv2是MOD意义下2的逆元,inv2=(MOD+1)/2
void FWT_or(int *a,int opt)
{
for(int i=1;i