量化交易:相关系数
作者:chen_h
微信号 & QQ:862251340
微信公众号:coderpai
相关系数是衡量两个变量之间的关系是线性时的程度。它的值总是在 -1 和 1 之间。正系数表示两个变量之间是直接相关的,即当一个变量增加时另一个变量也会增加。负系数表示变量是负相关的,所以当一个变量增加时,另一个变量相反会减少。相关系数等于 0 时,表示这两个变量是没有关系的。
两个系列 X 和 Y 的相关系数被定义为:
r=Cov(X,Y)std(X)std(Y) r = C o v ( X , Y ) s t d ( X ) s t d ( Y )
其中, Cov 表示协方差,std 表示标准方差。
两组随机数据的相关系数,大概率下是接近于 0 的。
相关性与协方差
相关性是协方差的归一化形式。它们在其他方面是相同的,并且在日常生活中经常被互相使用。在利用人类语言讨论这两种形式时,精确的使用显然是非常重要的,但从概念上来讲,它们又几乎是相同的。
协方差本身没有意义
假设我们有连个变量 X 和 Y,我们取这两个变量的协方差为:
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
X = np.random.rand(50)
Y = 2 * X + np.random.normal(0, 0.1, 50)
np.cov(X, Y)[0, 1]
输出结果为:0.14975887489776102
那么接下来怎么办呢?这又是什么意义呢?相关性使用序列 X 和 Y 的标准方差来归一化这个协方差,一旦我们将度量标准化为 -1 到 +1 之间时,我们就可以做出一些有意义的陈述了,并且进行相关的比较工作。
接下来,我们看看数据公式是如何推到的。
Cov(X,Y)std(X)std(Y) C o v ( X , Y ) s t d ( X ) s t d ( Y )
=Cov(X,Y)var(X)‾‾‾‾‾‾‾√var(Y)‾‾‾‾‾‾‾√ = C o v ( X , Y ) v a r ( X ) v a r ( Y )
=Cov(X,Y)Cov(X,X)‾‾‾‾‾‾‾‾‾‾√Cov(Y,Y)‾‾‾‾‾‾‾‾‾‾√ = C o v ( X , Y ) C o v ( X , X ) C o v ( Y , Y )
为了证明这两点,让我们来比较两个序列的相关性和协方差。
X = np.random.rand(50)
Y = 2 * X + 4
print 'Covariance of X and Y: \n' + str(np.cov(X, Y))
print 'Correlation of X and Y: \n' + str(np.corrcoef(X, Y))输出结果为:
Covariance of X and Y:
[[ 0.07228077 0.14456154]
[ 0.14456154 0.28912309]]
Correlation of X and Y:
[[ 1. 1.]
[ 1. 1.]]为什么 np.cov 和 np.corrcoef 都返回矩阵?
协方差均值是统计学中的一个重要概念。通常人们会参考两个变量 x 和 y的协方差,但实际上这只是 x 和 y 的协方差矩阵中的一个元素而已。对于每个输入变量,我们有一行和一列,交叉点就是这来那个变量的方差,或者协方差 cov(x,x)。让我们来检查一下,这个是否正确。
cov_matrix = np.cov(X, Y)
# We need to manually set the degrees of freedom on X to 1, as numpy defaults to 0 for variance
# This is usually fine, but will result in a slight mismatch as np.cov defaults to 1
error = cov_matrix[0, 0] - X.var(ddof=1)
print 'error: ' + str(error)输出结果为:error: 1.38777878078e-17
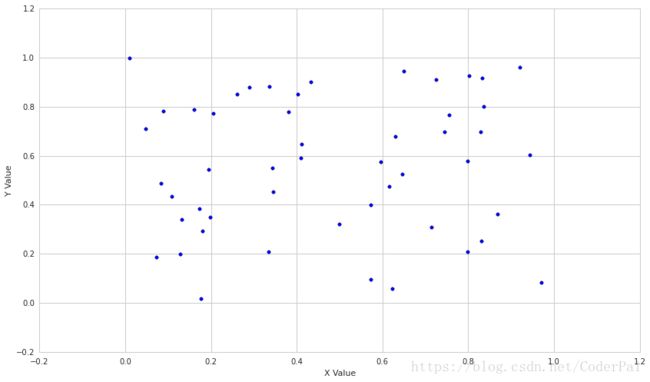
X = np.random.rand(50)
Y = np.random.rand(50)
plt.scatter(X,Y)
plt.xlabel('X Value')
plt.ylabel('Y Value')
# taking the relevant value from the matrix returned by np.cov
print 'Correlation: ' + str(np.cov(X,Y)[0,1]/(np.std(X)*np.std(Y)))
# Let's also use the builtin correlation function
print 'Built-in Correlation: ' + str(np.corrcoef(X, Y)[0, 1])输出结果为:
Correlation: 0.0612685087304
Built-in Correlation: 0.0600431385558现在让我们看看两组相关的数据是怎么样的。
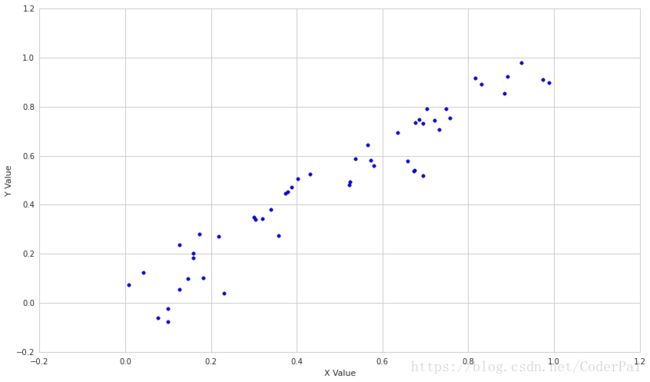
X = np.random.rand(50)
Y = X + np.random.normal(0, 0.1, 50)
plt.scatter(X,Y)
plt.xlabel('X Value')
plt.ylabel('Y Value')
print 'Correlation: ' + str(np.corrcoef(X, Y)[0, 1])输出结果为:Correlation: 0.958613485688
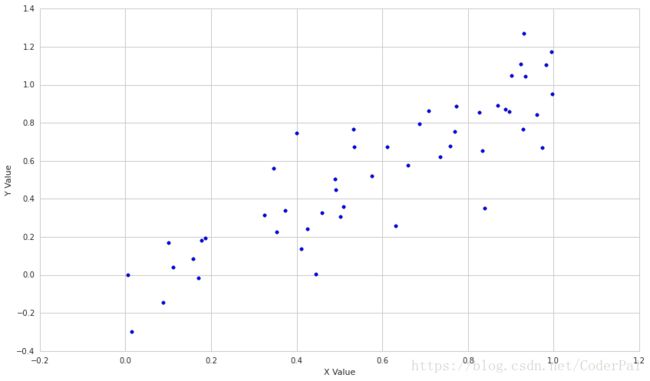
让我们通过加入更多的噪声来降低序列之间的相关性。
X = np.random.rand(50)
Y = X + np.random.normal(0, .2, 50)
plt.scatter(X,Y)
plt.xlabel('X Value')
plt.ylabel('Y Value')
print 'Correlation: ' + str(np.corrcoef(X, Y)[0, 1])输出结果为:Correlation: 0.879590392019
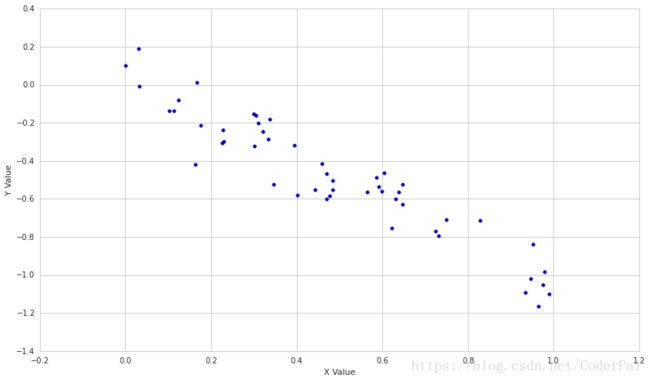
最后,让我们看看相关性相反的例子是什么样子的。
X = np.random.rand(50)
Y = -X + np.random.normal(0, .1, 50)
plt.scatter(X,Y)
plt.xlabel('X Value')
plt.ylabel('Y Value')
print 'Correlation: ' + str(np.corrcoef(X, Y)[0, 1])输出结果为:Correlation: -0.944604531847
我们看到有一些简单的误差,但很显然它们是相同的值。
这种关系在金融里有什么用处吗?
确定资产相关性
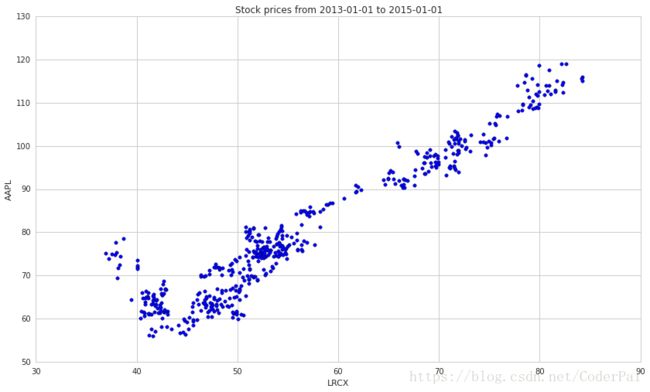
一旦我们确定两个系列是相关的,我可以使用这个特性来预测系列的未来价值。例如,让我们看看苹果公司和半导体设备制造商 Lam Research Corporation 之间价格的相关性。
# Pull the pricing data for our two stocks and S&P 500
start = '2013-01-01'
end = '2015-01-01'
bench = get_pricing('SPY', fields='price', start_date=start, end_date=end)
a1 = get_pricing('LRCX', fields='price', start_date=start, end_date=end)
a2 = get_pricing('AAPL', fields='price', start_date=start, end_date=end)
plt.scatter(a1,a2)
plt.xlabel('LRCX')
plt.ylabel('AAPL')
plt.title('Stock prices from ' + start + ' to ' + end)
print "Correlation coefficients"
print "LRCX and AAPL: ", np.corrcoef(a1,a2)[0,1]
print "LRCX and SPY: ", np.corrcoef(a1,bench)[0,1]
print "AAPL and SPY: ", np.corrcoef(bench,a2)[0,1]输出结果为:
Correlation coefficients
LRCX and AAPL: 0.954684674528
LRCX and SPY: 0.935191172334
AAPL and SPY: 0.89214568707构建不相关资产组合
相关性在金融领域用用的另一个原因是不相关的资产能产生最好的投资组合。对此的直觉是,如果资产不相关,那么一个资产的减值将不会与另一个资产的减值相对应。当许多不相关的资产合并时,这会导致非常稳定的回报。
限制
意义
很难严格确定相关性是否显著,尤其是当这些变量不是正态分布时。它们的相关系数接近于 1,我们可以说在这段时间内两只股票价格是非常相关的,这是相当安全的,但是这是否表示未来也是相关的呢?如果我们检查它们与标普 500 指数的相关性,我们会发现它也是相当高的。因此,AAPL 和 LRCX 之间的关联度比平均股票稍微高一点。
一个根本的问题是,通过选择正确的时间段来很容易的进行数据相关性。为了避免这种情况,我们应该计算很多历史时间段内两个量的相关性,并检查相关系数的分布。
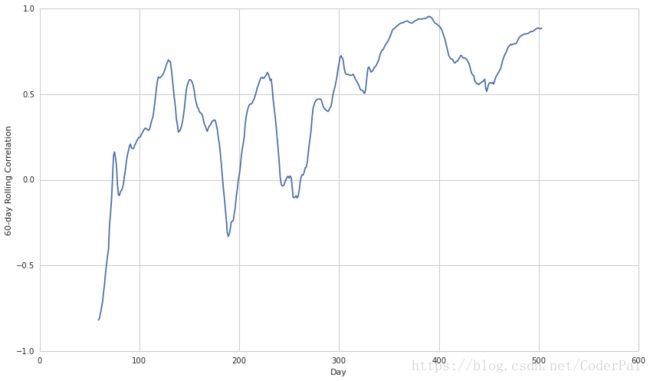
例如,请记住,2013年1月1日至2015年1月1日的AAPL与LRCX的相关性为0.95。 让我们来看看两者之间的滚动60天关联性,看看这是如何变化的。
rolling_correlation = pd.rolling_corr(a1, a2, 60)
plt.plot(rolling_correlation)
plt.xlabel('Day')
plt.ylabel('60-day Rolling Correlation')非线性关系
相关系数可用于检查两个变量之间的线性相关性。但是,我们要记住更重要的一点是,两个变量可能是以不同的,可预测的方式连接起来的,而不是这种单一线性的。例如,一个变量可能不会精确的遵守第二个变量的变化,两者之间会产生一定的随机延迟。或者直接两个变量就是非线性关系的。如果我们能检测到这种关系,那么在金融市场中是非常有意义的。
此外,相关系数可能会异常值非常敏感。这意味着即使包含活排除几个数据点也会改变我们的相关性,并且这些点是包含信息的,还是仅仅包含噪声的,我们并不是很清楚。
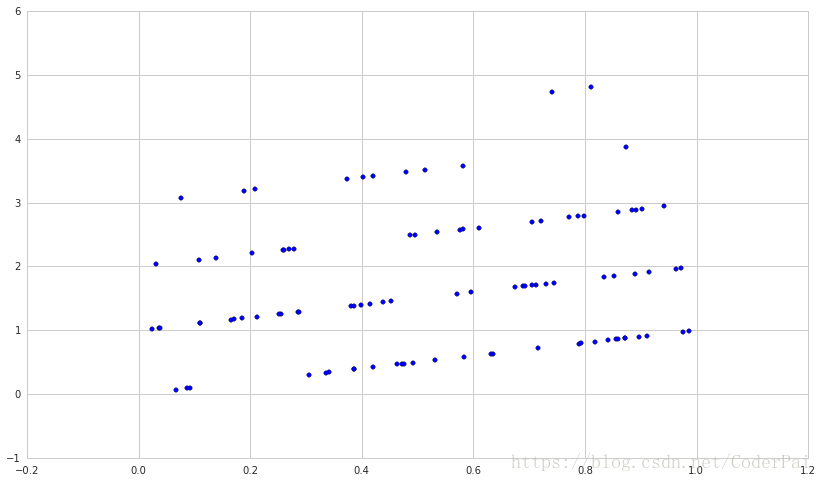
举一个例子,让我们的噪声分布时泊松分布的,而不是均衡分布,来看看会发生一些什么有意思的事。
X = np.random.rand(100)
Y = X + np.random.poisson(size=100)
plt.scatter(X, Y)
np.corrcoef(X, Y)[0, 1]输出结果为:0.18485889539744632
来源:quantopian