利用Python实现模糊动态聚类
利用Python实现模糊动态聚类
- 实验数据集
- 算法描述
- 1.数据规格化
- 2.构造模糊相似矩阵
- 3.求解模相似阵传递闭包
- 4.选取最优lambda分类
- 源代码
- 实验结果
- 1.特征指标矩阵
- 2.标准化后的特征指标矩阵
- 3.求模糊相似矩阵传递闭包
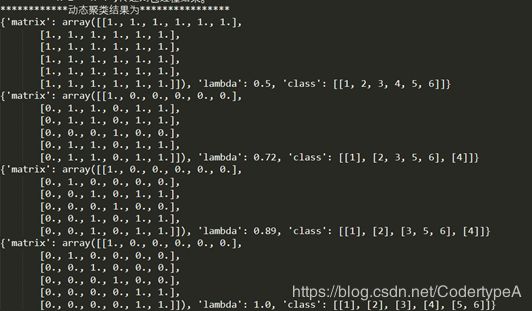
- 4.动态聚类结果
- 5.模糊动态图
- 6.Xie_Beni指标求解最佳lambda
实验数据集
**本实验选取了实验数据集的前六行。**
算法描述
1.数据规格化
此例采用标准化方法,对特征指标矩阵X的第j列,计算均值和方差,然后作变换
![]()
![]()
2.构造模糊相似矩阵
3.求解模相似阵传递闭包
此例采用平方法求取相似矩阵的传递闭包,从模糊相似矩阵R出发,依次求:R->R2 ->R4->…->Rn。
直到出现新的传递闭包等于上一次传递闭包的结果,算法终止。
4.选取最优lambda分类
此例采用Xie-Beni指标对作为lambda取值的评判标准:

XB指标寻找类内紧凑度和类间分离度之间的某个平衡点,其中
类内紧凑度 = 该公式分子部分/样本数m,越小越好。
类间分离度 = 该公式分母部分*样本数m,越大越好。
XB指标计算结果越小,聚类效果最好。
源代码
# -*- coding: utf-8 -*-
import numpy as np
import pprint
import xlrd
from copy import deepcopy
#矩阵不用科学计数法的显示方式
np.set_printoptions(suppress=True)
def main():
path = 'D:/煤层块段的特性指标值.xls'
# 0.读取数据
matrix = read_excel(path)
# 1.数据规范化:采用标准化方法
x_matrix = process_matrix(matrix)
# 2.构造模糊相似矩阵:采用夹角余弦法
r_matrix = get_rmatrix(x_matrix)
# 将模糊相似矩阵取两位小数,否则后面的与lambda值判断大小时会出错
for i in range(r_matrix.shape[0]) :
for j in range(r_matrix.shape[1]) :
r_matrix[i][j] = round(r_matrix[i][j],2)
print('==================特征指标矩阵================')
print(matrix)
print('===============标准化特征指标矩阵=============')
print(x_matrix)
print('==================模糊相似矩阵R================')
print(r_matrix)
# 3.求传递闭包t(R)
i = 0
while True:
t_r_matrix = get_tR(r_matrix)
print("==================模糊相似矩阵R^%d================"%(2**i))
print(t_r_matrix)
#若get_tR(r_matrix) == t_r_matrix ,退出循环
if (t_r_matrix == r_matrix).all():
print("******** R^%d = R^%d ,传递闭包过程结束。******** "%(2**(i-1),2**i))
break
#否则,将t_r_matrix作为待求闭包矩阵
else:
r_matrix = t_r_matrix
i += 1
# 4.按lambda截集进行动态聚类
result = lambda_clustering(t_r_matrix)
print("************动态聚类结果为****************")
for x in result:
pprint.pprint(x)
# 5.利用Xie_beni指数寻找最优分类
best_class = Xie_Beni(result,x_matrix)
print("***********最优分类结果如下***************")
print(best_class)
# 1.数据规范化:采用标准化方法
def process_matrix(x_matrix):
x = deepcopy(x_matrix)
#获得特征指标矩阵行列数
x_rows = x.shape[0]
x_cols = x.shape[1]
#参数0代表对每一列求均值,参数1代表对每一行求均值,无参数则求所有元素的均值
mean_matrix = np.mean(x,axis = 0)
var_matrix = np.var(x,axis = 0)
for i in range(x_rows):
for j in range(x_cols):
x[i][j] = (x[i][j] - mean_matrix[j])/var_matrix[j]
return x
# 2.构造模糊相似矩阵:采用夹角余弦法
def get_rmatrix(x_matrix):
x_rows = x_matrix.shape[0]
x_cols = x_matrix.shape[1]
# norm_matrix :每一行的2-范式值
norm_matrix = np.linalg.norm(x_matrix,axis = 1)
# r_matrix : 模糊相似矩阵
r_matrix = np.zeros((x_rows,x_rows),dtype = 'float')
#获得模糊相似接矩阵行列数
r_rows = r_matrix.shape[0]
r_cols = r_matrix.shape[1]
for i in range(r_rows):
for j in range(r_cols):
multi_matrix = x_matrix[i] * x_matrix[j]
r_matrix[i][j] = abs(np.dot(x_matrix[i],x_matrix[j])) / (norm_matrix[i] * norm_matrix[j])
return r_matrix
def get_tR(mat):
rows = mat.shape[0]
cols = mat.shape[1]
min_list = []
new_mat = np.zeros((rows,cols),dtype = 'float')
for m in range(rows):
for n in range(cols):
min_list = []
now_row = mat[m]
now_col = mat[:,n]
for k in range(len(now_row)):
min_cell = min(mat[m][k],mat[:,n][k])
min_list.append(min_cell)
new_mat[m][n] = max(min_list)
return new_mat
# 4.按lambda截集进行动态聚类
def lambda_clustering(final_matrix):
rows = final_matrix.shape[0]
cols = final_matrix.shape[1]
result = [] #返回的结果
lambda_list = [] #所有的lambda值
temp_matrix = np.zeros((rows,cols),dtype = 'float')
for i in final_matrix :
for j in i :
if j not in lambda_list :
lambda_list.append(j)
lambda_list.sort()
for i in range(len(lambda_list)):
class_list = [] #分类情况
mark_list = [] #存储当前lambda值,已经被分组的样本
temp_infor = {'matrix':np.zeros((rows,cols),dtype = 'float'),'lambda':lambda_list[i],'class':[]} #每个lambda值的分类情况
for m in range(rows):
for n in range(cols):
if final_matrix[m][n] >= lambda_list[i]:
temp_infor['matrix'][m][n] = 1
else:
temp_infor['matrix'][m][n] = 0
for m in range(rows):
if (m+1) in mark_list:
continue
now_class = []
now_class.append(m+1)
mark_list.append(m+1)
for n in range(m+1,rows):
if (temp_infor['matrix'][m] == temp_infor['matrix'][n]).all() :
now_class.append(n+1)
mark_list.append(n+1)
class_list.append(now_class)
temp_infor['class'] = class_list
result.append(temp_infor)
return result
#print("===============t(R)%f==========="%lambda_list[i])
#print(temp_matrix)
def Xie_Beni(infor_list,x_matrix):
class_num = 0 #当前总类数
class_list = [] #当前分类情况
result = [] #返回结果
rate = 0 #Xie_Beni指数
flag = 0 #标记Xie_Beni指数最大的分类情况
for temp in infor_list:
this_in_measure = 0 #当前分类的类内紧密度,类中各点与类中心的距离平方和
this_out_measure = 100000 #当前分类的类间分离度,最小的类与类中心的平方
result_infor = {'class':[],'in':0,'out':0} #每一种分类生成一个 class-in-out字典,最后append到result中用作函数返回值
class_list = temp['class']
class_num = len(class_list)
means_list = [np.zeros((1,x_matrix.shape[1]),dtype = 'float')]*class_num #该分类下,每一类的均值
#遍历每一类
for i in range(class_num):
#求每一类的类中心
this_class_num = len(class_list[i])
this_sum = np.zeros((1,x_matrix.shape[1]),dtype = 'float')
this_means = np.zeros((1,x_matrix.shape[1]),dtype = 'float')
for j in range(this_class_num):
this_sum += x_matrix[class_list[i][j]-1]
this_means = this_sum/this_class_num
means_list[i] = this_means
#计算当前分类类间分离度
for m in range(len(means_list)):
#当所有样本分为一类的时候,类间分离度为无穷大,但这样的分类没有任何意义,所以置0,不予以比较。
if len(means_list) == 1:
this_out_measure = 0
break
for n in range(m+1,len(means_list)):
temp = fun(means_list[m],means_list[n])
if temp < this_out_measure:
this_out_measure = temp
#计算当前分类类内紧密度
for m in range(class_num):
this_class_num = len(class_list[i])
for n in range(this_class_num):
add = fun(means_list[m],np.array([x_matrix[n-1]]))
this_in_measure += add
#print(this_in_measure)
#print(this_out_measure)
this_rate = this_out_measure/this_in_measure
print("当前分类情况为")
print(class_list)
print("Xie_Beni指数为%f"%this_rate)
print("==============================")
if this_rate > rate:
rate = this_rate
flag = class_list
return flag
#计算向量间距离,本题采用二范式
def fun(x1,x2):
distance = 0
if len(x1) != len(x2):
print("输入的矩阵有误")
return False
temp_x = x1 - x2
for i in range(len(x1)):
increase = temp_x[0,i]**2
distance += increase
return distance
#传入excel目录
def read_excel(path):
#打开exel
workbook = xlrd.open_workbook(path,'r')
#获得sheet1名字
sheet1 = workbook.sheets()[0]
rows = sheet1.nrows
cols = sheet1.ncols
#建立特征指标矩阵
x_matrix = np.zeros((rows-1,cols-1),dtype = 'float')
#第一行是列名,从第二行开始
for i in range(0,rows-1):
#第一列是序号,从第二列开始
for j in range(0,cols-1):
x_matrix[i][j]= sheet1.cell(i+1,j+1).value
return x_matrix
if __name__ == '__main__':
main()