【搜索算法】八数码问题的多种解法
目录
-
八数码问题简介
-
判断是否有解
-
朴素的 DFS 和 BFS
-
对于 DFS 和 BFS 剪枝 (去重)
- 数据结构 map
- 康托展开
-
双向BFS
-
A*算法
-
IDA算法 - 迭代加深的DFS
-
输出路径的方法
八数码问题简介:
在 3×3 的棋盘上,摆有八个棋子,每个棋子上标有1至8的某一数字。
棋盘中留有一个空格,空格用0来表示。空格周围的棋子可以移到空格中。
要求解的问题是: 给出一种初始布局(初始状态)和目标布局,找到一种最少步骤的移动方法,实现从初始布局到目标布局的转变
(为了简化棋盘,我们把每个数字按每行缩成一个长串)
| Input | 初始:123456780 目标:087654321 | 初始:123456780 目标:123456708 | 初始:123456780 目标:123456870 | 初始:123456780 目标:123456780 |
|---|---|---|---|---|
| Ouput | 28 | 1 | No solve | 0 |
比 如 说 : [ 1 2 3 4 5 6 7 8 0 ] ⟶ 1 步 [ 1 2 3 4 5 6 7 0 8 ] 比如说: \left[\begin{matrix}1 & 2 & 3 \\4 & 5 & 6\\7 & 8 & 0\\\end{matrix}\right]\stackrel{1步}\longrightarrow\left[\begin{matrix}1 & 2 & 3 \\4 & 5 & 6\\7 & 0 & 8\\\end{matrix}\right] 比如说:⎣⎡147258360⎦⎤⟶1步⎣⎡147250368⎦⎤
比 如 说 : [ 1 2 3 4 5 6 7 8 0 ] ⟶ 28 步 [ 0 8 7 6 5 4 3 2 1 ] 比如说:\left[\begin{matrix}1 & 2 & 3 \\4 & 5 & 6\\7 & 8 & 0\\\end{matrix}\right]\stackrel{28步}\longrightarrow\left[\begin{matrix}0 & 8 & 7 \\6 & 5 & 4\\3 & 2 & 1\\\end{matrix}\right] 比如说:⎣⎡147258360⎦⎤⟶28步⎣⎡063852741⎦⎤
比 如 说 : [ 1 2 3 4 5 6 7 8 0 ] ⟶ N U L L [ 1 2 3 4 5 6 8 7 0 ] 比如说:\left[\begin{matrix}1 & 2 & 3 \\4 & 5 & 6\\7 & 8 & 0\\\end{matrix}\right]\stackrel{NULL}\longrightarrow\left[\begin{matrix}1 & 2& 3 \\4 & 5 & 6\\8 & 7 & 0\\\end{matrix}\right] 比如说:⎣⎡147258360⎦⎤⟶NULL⎣⎡148257360⎦⎤
判断是否有解:
这是一个非常经典的搜索问题,但是有时候我们会发现从 初始状态 到达不了 目标状态 ,这时候我们就需要提前判断是否有解 ( 不然无解的时候搜索算法会一直搜 )
先说结论:
把棋盘状态表示成一维的形式,求出除 0 之外所有数字的逆序数之和,称为这个状态的逆序
(也就是每个数字前面比它大的数字的个数的和)
若两个状态的逆序 奇偶性相同 ,则 可相互到达,否则 不可相互到达
例如: 123456780 和 213456780
逆序对和数为 28 和 27
所以无法互相到达
证明:
证明其必要性: 如果两个状态逆序对的和奇偶性不同,则必然不能互相抵达
首先,对于 3 × 3 3\times3 3×3 的格子,当 0 0 0 元素与任意元素交换(进行移动),表现在压缩之后的长串数字上分别是:
左移:将 0 0 0 与前一位交换,此时总逆序奇偶性不变
因为 0 0 0 本身不算在逆序对计算内,总体顺序没有改变
右移:将 0 0 0 与后一位交换,同左移
上移:将 0 0 0 与前第三位交换,此时总逆序奇偶性不变
假设被 0 0 0 交换元素是 A,中间元素有两个,分别是B,C
- 如果有 A>B 和 A>C 则总体逆序对个数 -2 ,奇偶性不变
- 如果有 A>B 和 A
- 如果有 AC 同理 2
- 如果有 A
下移:将 0 0 0 与后第三位交换,同上移
证明其充分性: 如果两个状态逆序对的和奇偶性相同,则必定可以互相抵达
看 状 态 : [ A B C 0 D E F G H ] ⟶ 11 步 [ A B 0 C D E F G H ] 看状态: \left[\begin{matrix}A& B & C\\0 & D & E\\F & G & H\\\end{matrix}\right]\stackrel{11步}\longrightarrow\left[\begin{matrix}A& B & 0\\C & D & E\\F & G & H\\\end{matrix}\right] 看状态:⎣⎡A0FBDGCEH⎦⎤⟶11步⎣⎡ACFBDG0EH⎦⎤
可以看到这两个状态是可以相互抵达的
对应: A B C 0 D E F G H ⟶ A B 0 C D E F G H A B C 0 D E F G H \longrightarrow A B 0 C D E F G H ABC0DEFGH⟶AB0CDEFGH
其他左右移同理
也就是说任意 左移和右移 的步骤都可以相互抵达,又因为左移和右移不改变逆序对奇偶性
则有
可以将所有偶数逆序对和的状态转化成:0 1 2 3 4 5 6 7 8
可以将所有奇数逆序对和的状态转化成:0 2 1 3 4 5 6 7 8
因为根据前面的左右移无限制证明,你可以通过有限次操作将最大的元素放在最后面,同时把次大的元素放在倒数第二位而不打乱最后一位,前推同理,直到达到状态 0 1 2 和 0 2 1 此时因为位数限制,无法继续这样操作,所以证得
同样的由于所有偶状态和所有奇状态都收束与不同的一个状态,根据移动的可逆性,故如果两个状态逆序对的和奇偶性相同,则必定可以互相抵达
代码:
int P(string S){
int jShu = 0;
for(int i=0; i<9; i++) for(int j=0; j<i; j++) if(S[i]>S[j]&&S[j]!='0') jShu++;
return jShu; //返回逆序对和,把两个状态的逆序对和都%2,相等则有解,不等则无解
}
朴素的 DFS 和 BFS:
判断了是否有解,接下来就是看如何搜索,总所周知,最基础的搜索算法有两种: 深搜(DFS) 和 广搜(BFS)
对于朴素的DFS和BFS而言,显然这道题用广搜更好,因为是找最小步骤,如果是深搜,如果不知道最小步数限制,则会一直在一个分支中搜索,而且第一次搜到的解未必是最小解,而广搜则会更快地找到最小解 ( 因为是平铺的往下搜,所以第一次碰到的解一定是最小解 ),所以说在这里只贴朴素BFS的代码
朴素BFS:
可以用,但由于没有判重,大步数会超时(甚至死循环
例如:
123456780
087654321
28
inti.h头文件代码传送
#include"init.h"
queue<string> NS; //记录字符的队列
queue<int> Zhixy; //记录步数,0的位置压缩后的队列
int MinZhi;
int main(){
if(Init()){
cout<<"No Solve"<<endl;
return 0;
}
NS.push(S);
for(int i=0; i<9; i++) if(S[i]=='0') Zhixy.push((int)(i/3)*10+i%3);
while(!NS.empty()){
string S2 = NS.front(); NS.pop();
int A = Zhixy.front(); Zhixy.pop();
int Zhi = A/100, x = (A/10)%10, y = A%10;
//用了数据压缩,Zhi代表目前状态到原状态步数,x和y代表现在0的位置,把它们压成一个数存进队列节约空间
if(S2==S_Goal){ //找到即可退出,必定是最短
MinZhi = Zhi;
break;
}
if(x+1<3){
NS.push(exChange(S2, x+1, y, x, y));
Zhixy.push((x+1)*10+y+(Zhi+1)*100);
}
if(y+1<3){
NS.push(exChange(S2, x, y+1, x, y));
Zhixy.push(x*10+y+1+(Zhi+1)*100);
}
if(x-1>=0){
NS.push(exChange(S2, x-1, y, x, y));
Zhixy.push((x-1)*10+y+(Zhi+1)*100);
}
if(y-1>=0){
NS.push(exChange(S2, x, y-1, x, y));
Zhixy.push(x*10+y-1+(Zhi+1)*100);
}
}
cout<<MinZhi<<endl;
TimeB("传统BFS算法");
string B = S_Goal;
return 0;
}
头文件的代码:
因为每个程序有一部分代码是完全一样的,所以就改成头文件了XD
#include
对于 DFS 和 BFS 剪枝 (去重)
对于这两个搜索来说,很显然有一个优化方法:
BFS:如果当前状态我以前搜过,那么我就不需要继续搜这个状态
DFS:如果当前状态我以前搜过,且当前状态步数比我以前搜到这个状态用的步数多,则不继续往下搜,反之则还是需要往下搜
这样去重以后,不仅可以大幅节省搜索时间,也可以避免死循环的产生
那么怎么判断当前状态是否搜过呢?
Map数据结构:
C++为我们提供了一个非常方便的数据结构Map,至于Map是什么,该怎么用
可以看这位前辈博客:https://blog.csdn.net/qq_39836658/article/details/78560819
(另外实际Map由于各种原因,速度是稍微慢一点的,但对于解八数码问题已经绰绰有余了)
使用Map的DFS:
需要限制最大搜索深度,这里限制深度30层,挺慢的,一般都会超时
剪枝思路: 如果当前状态我以前搜过,且当前状态步数比我以前搜到这个状态用的步数多,则不继续往下搜,反之则还是需要往下搜
inti.h头文件代码传送
#include"init.h"
map<string, int> Map;
int MinZhi = 30;
void DFS(int jShu, string S2, int x, int y){
if(S2==S_Goal){
if(MinZhi>jShu) MinZhi = jShu;
return;
}
//去重部分
if(Map.count(S2)){
if(Map[S2]>jShu) Map[S2] = jShu;
else return;
}
else Map[S2] = jShu;
if(jShu>=MinZhi) return;
string Bet = S2;
if(x+1<3){
S2 = exChange(S2, x+1, y, x, y);
DFS(jShu+1, S2, x+1, y);
S2 = Bet;
}
if(y+1<3){
S2=exChange(S2, x, y+1, x, y);
DFS(jShu+1, S2, x, y+1);
S2 = Bet;
}
if(x-1>=0){
S2=exChange(S2, x-1, y, x, y);
DFS(jShu+1, S2, x-1, y);
S2 = Bet;
}
if(y-1>=0){
S2=exChange(S2, x, y-1, x, y);
DFS(jShu+1, S2, x, y-1);
S2 = Bet;
}
}
int main(){
if(Init()){
cout<<"No Solve"<<endl;
return 0;
}
int x, y;
for(int i=0; i<9; i++) if(S[i]=='0') x=i/3, y=i%3;
DFS(0, S, x, y);
cout<<MinZhi<<endl;
TimeB("传统DFS+Map");
}使用Map的BFS:
inti.h头文件代码传送
剪枝思路: 如果当前状态我以前搜过,那么我就不需要继续搜这个状态,同样的,第一次搜到的相同状态一定是最短解
#include"init.h"
map<string, int> Map;
map<string, string> Map2;
queue<string> NS;
queue<int> Zhixy;
int MinZhi;
int main(){
if(Init()){
cout<<"No Solve"<<endl;
return 0;
}
NS.push(S);
for(int i=0; i<9; i++) if(S[i]=='0') Zhixy.push((int)(i/3)*10+i%3);
while(!NS.empty()){
string S2 = NS.front(); NS.pop();
int A = Zhixy.front(); Zhixy.pop();
int Zhi = A/100, x = (A/10)%10, y = A%10;
if(S2==S_Goal){
MinZhi = Zhi;
break;
}
//去重部分
if(Map.count(S2)) continue;
else Map[S2] = Zhi;
if(x+1<3){
NS.push(exChange(S2, x+1, y, x, y));
Zhixy.push((x+1)*10+y+(Zhi+1)*100);
}
if(y+1<3){
NS.push(exChange(S2, x, y+1, x, y));
Zhixy.push(x*10+y+1+(Zhi+1)*100);
}
if(x-1>=0){
NS.push(exChange(S2, x-1, y, x, y));
Zhixy.push((x-1)*10+y+(Zhi+1)*100);
}
if(y-1>=0){
NS.push(exChange(S2, x, y-1, x, y));
Zhixy.push(x*10+y-1+(Zhi+1)*100);
}
}
cout<<MinZhi<<endl;
TimeB("传统BFS算法+Map");
return 0;
}康托(cantor)展开:
竟然Map速度不算很快,那我们有什么其它方法来解决去重问题,其实在使用Map时,我们已经用到了Hash,那么对于八数码问题,很显然我们看出所有的棋盘状态其实就是 0~8 的全排列,而对于全排列的Hash,我们可以采用 康托展开
康托展开 是一个全排列到一个自然数的双射,常用于构建哈希表时的空间压缩
康托展开 的实质是计算当前排列在所有由小到大全排列中的位次,而且是可逆的
例如 012345678 就是 0;102345678 就是 1
那么如何对一组数进行康托展开?
有 公 式 : V = ∑ i = 1 n A i × ( n − i ) ! 有公式: V = \sum_{i=1}^nA_i \times (n-i)! 有公式:V=i=1∑nAi×(n−i)! V V V 代表最后得到的 H a s h Hash Hash值
n n n 代表目标的元素个数
A i A_i Ai 代表第 i i i 个元素后面比此元素小的元素个数
代码:
int Factorial[9]={1, 1, 2, 6, 24, 120, 720, 5040, 40320}; //康托函数需要的阶乘
int Cantor(string S){ //康拓函数
int jShu = 0;
for(int i=0; i<9; i++){
int jShu2 = 0;
for(int j=i+1; j<9; j++) if(S[i]>S[j]) jShu2++;
jShu += jShu2*Factorial[8-i];
}
return jShu;
}具体实现代码就不贴了XD
成效:
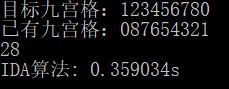
DFS用Cantor展开快了不少,甚至有希望避免TLE的悲惨命运Orz,然而还是有限深
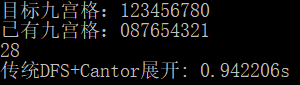
BFS发挥稳定,快了一点:
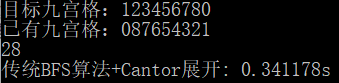
双向BFS搜索:
介绍待更…
inti.h头文件代码传送
下面是用 Map 去重的代码:
#include"init.h"
map<string, int> Map;
queue<string> NS;
queue<int> Zhixy;
int MinZhi;
int main(){
if(Init()){
cout<<"No Solve"<<endl;
return 0;
}
NS.push(S+"2"); NS.push(S_Goal+"1");
for(int i=0; i<9; i++) if(S[i]=='0') Zhixy.push(100+(int)(i/3)*10+i%3);
for(int i=0; i<9; i++) if(S_Goal[i]=='0') Zhixy.push(100+(int)(i/3)*10+i%3);
while(!NS.empty()){
string S1 = NS.front();
NS.pop();
bool sign = S1[9]-'1';
string S2(S1.substr(0,9)); //有点乱,有时间我整理一下吧
int A = Zhixy.front();
Zhixy.pop();
int Zhi = A/100, x = (A/10)%10, y = A%10;
if(Map.count(S2)){
int bet = Map[S2];
if((sign&&bet<0)||(!sign&&bet>0)){
cout<<Zhi+abs(Map[S2])-2<<endl;
break;
}
else if(abs(bet)>Zhi){
if(sign) Map[S2] = Zhi;
else Map[S2] = -Zhi;
}
else continue;
}
else{
if(sign){
Map[S2] = Zhi;
S2 = S2+"2";
}
else{
Map[S2] = -Zhi;
S2 = S2+"1";
}
}
if(x+1<3){
NS.push(exChange(S2, x+1, y, x, y));
Zhixy.push((x+1)*10+y+(Zhi+1)*100);
}
if(y+1<3){
NS.push(exChange(S2, x, y+1, x, y));
Zhixy.push(x*10+y+1+(Zhi+1)*100);
}
if(x-1>=0){
NS.push(exChange(S2, x-1, y, x, y));
Zhixy.push((x-1)*10+y+(Zhi+1)*100);
}
if(y-1>=0){
NS.push(exChange(S2, x, y-1, x, y));
Zhixy.push(x*10+y-1+(Zhi+1)*100);
}
}
TimeB("双向BFS算法");
return 0;
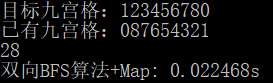
}讲道理,双向BFS能这么快真是超出我的想象了,估计是因为数据特殊的原因
A*算法:
A*算法 可以通过当前节点状态和以后预估的状态来有选择的拓展节点,从而更快的抵达搜索目标
具体公式表现为: f ∗ ( n ) = g ∗ ( n ) + h ∗ ( n ) f^*(n)=g^*(n)+h^*(n) f∗(n)=g∗(n)+h∗(n) f ∗ ( n ) f^*(n) f∗(n) 代表对节点 n 评估结果
g ∗ ( n ) g^*(n) g∗(n) 代表原始节点到当前节点 n 的实际步数
h ∗ ( n ) h^*(n) h∗(n) 代表当前节点 n 到目标节点的估计步数,我们称之为 启式发函数
值得注意的是,我们把 h ( n ) h(n) h(n) 代表为当前节点到目标节点的实际步数
那么可以证明如果有 h ∗ ( n ) ≤ h ( n ) h^*(n)\leq h(n) h∗(n)≤h(n) 则必定可以找到最优解,同样的,如果 h ∗ ( n ) h^*(n) h∗(n) 越接近 h ( n ) h(n) h(n),则搜索效率越高
- 当 h ∗ ( n ) = h ( n ) h^*(n)= h(n) h∗(n)=h(n) 时,拥有最高的效率
- 当 h ∗ ( n ) = 0 h^*(n)= 0 h∗(n)=0 时,将退化成 Dijkstra算法
- 当 h ∗ ( n ) > h ( n ) h^*(n)> h(n) h∗(n)>h(n) 时,可以很快的搜索到目标,但是未必是最优解
那么对于八数码问题,我们可以设定多种启发式函数:
- h ∗ ( n ) = 当 前 状 态 和 目 标 状 态 格 子 上 不 同 的 数 字 个 数 h^*(n) = 当前状态和目标状态格子上不同的数字个数 h∗(n)=当前状态和目标状态格子上不同的数字个数
- h ∗ ( n ) = 当 前 状 态 的 0 跟 目 标 状 态 的 0 相 距 的 格 数 h^*(n) = 当前状态的 0 跟目标状态的 0 相距的格数 h∗(n)=当前状态的0跟目标状态的0相距的格数
- 还 有 很 多 , 常 用 的 是 上 面 两 种 还有很多,常用的是上面两种 还有很多,常用的是上面两种
使用第一种启发式函数的A*算法代码:
代码介绍待更
inti.h头文件代码传送
#include"init.h"
struct Node{
int Fn, Num;
string S1;
bool operator < (const Node & a) const{ return Fn>a.Fn; }
};
int Compare(string a, string b){
int jShu = 0;
for(int i=0; i<9; i++) if(a[i]!=b[i]) jShu++;
return jShu;
}
priority_queue<Node> NS;
map<string, int> Map;
int main(){
if(Init()){
cout<<"No Solve"<<endl;
return 0;
}
Node Head;
Head.Fn = 0; Head.S1 = S;
for(int i=0; i<9; i++) if(S[i]=='0') Head.Num = (int)(i/3)*10+i%3;
NS.push(Head);
while(!NS.empty()){
Node b, a = NS.top(); NS.pop();
int Zhi = a.Num/100, x = (a.Num/10)%10, y = a.Num%10;
if(a.S1 == S_Goal){
cout<<Zhi<<endl;
break;
}
if(Map.count(a.S1)){
if(Map[a.S1]>Zhi) Map[a.S1] = Zhi;
else continue;
}
else Map[a.S1] = Zhi;
if(x+1<3){
b.S1 = exChange(a.S1, x+1, y, x, y);
b.Fn = Zhi + Compare(b.S1, S_Goal);
b.Num = (x+1)*10+y+(Zhi+1)*100;
NS.push(b);
}
if(y+1<3){
b.S1 = exChange(a.S1, x, y+1, x, y);
b.Fn = Zhi + Compare(b.S1, S_Goal);
b.Num = x*10+y+1+(Zhi+1)*100;
NS.push(b);
}
if(x-1>=0){
b.S1 = exChange(a.S1, x-1, y, x, y);
b.Fn = Zhi + Compare(b.S1, S_Goal);
b.Num = (x-1)*10+y+(Zhi+1)*100;
NS.push(b);
}
if(y-1>=0){
b.S1 = exChange(a.S1, x, y-1, x, y);
b.Fn = Zhi + Compare(b.S1, S_Goal);
b.Num = x*10+y-1+(Zhi+1)*100;
NS.push(b);
}
}
TimeB("A_Star算法+Map");
return 0;
}有一些优化,但是不是非常明显,当然如果有更好的启发式函数会更快

迭代加深搜索:
迭代加深搜索实际上就是逐渐加大限制深度的DFS搜索
比如说对于八数码问题,由于不知道最大深度,我们只能提前预定一个最大的迭代深度,但这样对于解规模较小的答案,相当于浪费了大量时间搜索到最大迭代深度
所以说我们可以在搜索中 逐渐加大迭代深度
比如说:
- 开始迭代深度为 1,搜索一次,没有解就退出
- 之后迭代深度为 2,搜索一次,没有解就退出
- …
- 最后迭代深度为 n,搜索一次,有解,则最短步数为 n
那么为什么不用 BFS 而用 迭代加深搜索 呢?
首先,迭代加深搜索不像DFS一样,需要大量空间来存储要遍历的节点
其次,迭代加深搜索看似时间复杂度很高 (因为不断的重复搜索),但实际上它的时间复杂度跟 BFS 是相同的
举个简单的例子说明,假如说每个节点可以扩展两个节点
对于 BFS 来讲,第 n n n 层的拓展节点数是 2 n 2^n 2n
而对于 迭代加深搜索 来讲,第一次扩展的节点数是 1 = 2 1 − 1 1=2^1-1 1=21−1,第二次扩展的节点数是 1 + 2 = 2 2 − 1 1+2=2^2-1 1+2=22−1,第 n − 1 n-1 n−1 次拓展的节点数是 2 n − 1 − 1 2^{n-1}-1 2n−1−1
其前 n n n 次拓展的节点数和为 2 n − 2 n 2^n-2n 2n−2n,也就是说重复的遍历以前的节点代价相对于拓展下一层来说并不高,对于每个节点可以拓展更多节点的情况更是如此
迭代加深搜索代码:
加入了剪枝,具体细节会在以后更新
#include"init.h"
int jShu;
bool B;
int Compare(string a, string b){
int jShu2 = 0;
for(int i=0; i<9; i++) if(a[i]!=b[i]) jShu2++;
return jShu2;
}
void IDA(int jShu2, string S2, int x, int y, int u){
if(S2==S_Goal){
B=1;
return;
}
if(B) return;
if(Compare(S2, S_Goal) + jShu2 - 1>jShu) return;
string S3;
if(x+1<3&&u!=3){
S3 = S2;
IDA(jShu2+1, exChange(S3, x+1, y, x, y), x+1, y, 0);
}
if(y+1<3&&u!=2){
S3 = S2;
IDA(jShu2+1, exChange(S3, x, y+1, x, y), x, y+1, 1);
}
if(x-1>=0&&u!=0){
S3 = S2;
IDA(jShu2+1, exChange(S3, x-1, y, x, y), x-1, y, 3);
}
if(y-1>=0&&u!=1){
S3 = S2;
IDA(jShu2+1, exChange(S2, x, y-1, x, y), x, y-1, 2);
}
}
int main(){
if(Init()){
cout<<"No Solve"<<endl;
return 0;
}
int x, y;
for(int i=0; i<9; i++) if(S[i]=='0') x=i/3, y=i%3;
while(1){
IDA(0, S, x, y, -1);
if(B){
cout<<jShu<<endl;
break;
}
jShu++;
}
TimeB("IDA算法");
return 0;
}