前面文章中在分析push_transactioneos源码赏析(二十):EOS智能合约之push_transaction的天龙八“步”以及区块签名eos源码赏析(二十一):EOS智能合约之区块签名的天龙八“步”的时候都提到了默克尔树,受限于篇幅未做具体分析。今天我们来谈谈默克尔树在eos中的应用。拟分为上下两篇,上篇主要分为以下内容:
默克尔树简介
eos中如何构建默克尔树
1、默克尔树简介
关于Merkle树的介绍博客园有位大牛写的很仔细,强烈建议进行阅读。可以参考这里:http://www.cnblogs.com/fengzhiwu/p/5524324.html
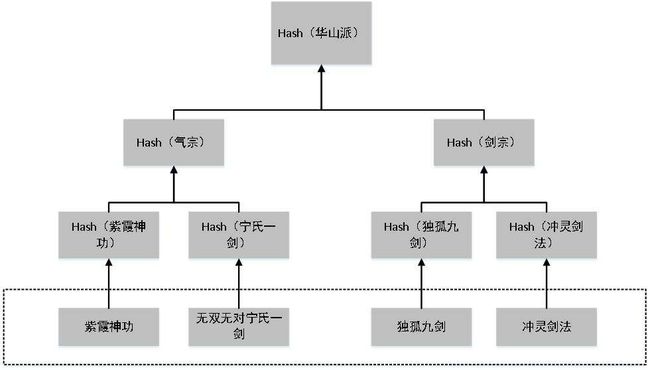
由于侧重点不同,我们不再进行一一解释,我们尝试用通俗的语言来解释下如何构建一个Merkle树。读过《笑傲江湖》原著或者看过《笑傲江湖》影视剧的朋友们对华山派应该都不陌生,华山派由于种种原因分成了气宗和剑宗两派,而我们所熟知的“君子剑”岳不群便是气宗的代表人物,而老前辈风清扬是剑宗的代表人物,下面以气宗和剑宗的代表武功来说明如何构建一个默克尔树:
Merkle Tree可以看做Hash List的泛化(Hash List可以看作一种特殊的Merkle Tree,即树高为2的多叉Merkle Tree)。在最底层,和哈希列表一样,我们把数据分成小的数据块,这里我们选取了华山派气宗和剑宗的代表武功紫霞神功、无双无对宁氏一剑、独孤九剑、冲灵剑法(不要问我为什么选这个,就是觉得好听),往上一层我们分别对这四种武功进行一次hash,在eos中也就是使用sha256中的hash转换为64位的数据。但是往上走,并不是直接去运算根哈希,而是把相邻的两个哈希合并成一个字符串,然后运算这个字符串的哈希,例如剑宗中的独孤九剑和冲灵剑法不是直接hash,而是将两者的hash合并成一个字符串再进行hash,在往上依旧如此。这样便形成了华山派的hash值。
那么有的朋友可能会问:玉女十九剑这个武功是剑宗还是气宗分不清怎么办,我们是该把它当成气宗还是剑宗呢?我们可以把它单独拿出来进行hash,也就是最底层的数据块出现奇数的情况下,可以这样进行构建默克尔树:
如果最底层武功数量是奇数,那到最后必然出现一个单身哈希,这种情况就直接对玉女十九剑进行哈希运算,所以也能得到它的子哈希。于是往上推,依然是一样的方式,可以得到数目更少的新一级哈希,最终必然形成一棵倒挂的树,到了树根的这个位置,这一代就剩下一个根哈希了,我们把它叫做 Merkle Root,也就是我们的华山派的hash值。
2、eos中如何构建默克尔树
我们知道在eos中最重要的因素无非区块(block)、事物(transaction)、动作(action),通过阅读源码我们会发现,在每一次transaction执行的过程中都会对transaction和action进行默克尔树的构建,我们来一步步看一下。
当transaction被打包到区块中之后会有一个区块信息的确认,即:finalize_block,我们来看:
1void finalize_block()
2 {
3 //该方法开始对一些资源信息进行确认操作
4 //我们接下来加了部分日志打印,方便观察对比
5 std::string strPending = "";
6 strPending = fc::json::to_string(*pending->_pending_block_state);
7 dlog("contorller before set action merkle:${state}", ("state", strPending));
8 set_action_merkle();
9 strPending = fc::json::to_string(*pending->_pending_block_state);
10 dlog("contorller after set action and before set trx merkle:${state}", ("state", strPending));
11 set_trx_merkle();
12 strPending = fc::json::to_string(*pending->_pending_block_state);
13 dlog("contorller after set trx merkle:${state}", ("state", strPending));
14
15 auto p = pending->_pending_block_state;
16 p->id = p->header.id();
17
18 create_block_summary(p->id);
19
20 } FC_CAPTURE_AND_RETHROW() }
在这里面我们看到了set_action_merkle以及set_trx_merkle对action以及transaction进行默克尔树的构建,继续来看:
1 void set_action_merkle() {
2 vector action_digests;
3 dlog("contorller set_action_merkle size:${size}", ("size", pending->_actions.size()));
4 action_digests.reserve( pending->_actions.size() );
5 for( const auto& a : pending->_actions )
6 action_digests.emplace_back( a.digest() );
7
8 pending->_pending_block_state->header.action_mroot = merkle( move(action_digests) );
9 }
10
11 void set_trx_merkle() {
12 vector trx_digests;
13 const auto& trxs = pending->_pending_block_state->block->transactions;
14 dlog("contorller set_trx_merkle size:${size}", ("size", trxs.size()));
15 trx_digests.reserve( trxs.size() );
16 for( const auto& a : trxs )
17 trx_digests.emplace_back( a.digest() );
18
19 pending->_pending_block_state->header.transaction_mroot = merkle( move(trx_digests) );
20 }
不管是set_action_merkle还是set_trx_merkle最后都调用了Merkle方法,即先获取action或者transaction的摘要信息,然后进行默克尔树的构建,我们来看Merkle函数,在Merkle.cpp中:
1digest_type merkle(vector ids) {
2 if( 0 == ids.size() ) { return digest_type(); }
3
4 while( ids.size() > 1 ) {
5 if( ids.size() % 2 )
6 ids.push_back(ids.back());
7
8 for (int i = 0; i < ids.size() / 2; i++) {
9 ids[i] = digest_type::hash(make_canonical_pair(ids[2 * i], ids[(2 * i) + 1]));
10 }
11
12 ids.resize(ids.size() / 2);
13 }
针对武功个数是奇数还是偶数分别进行了hash,最终形成了默克尔树的构建,我这里以创建用户名为例,根据日志的打印对其进行跟踪对比结果,先执行命令行如下:
1cleos create account eosio merkletest yourpubkey yourpubkey
在构建默克尔树之前和之后的对比结果如下:
1//构建默克尔树之前
2 "header": {
3 "timestamp": "2018-10-10T12:32:30.500",
4 "producer": "eosio",
5 "confirmed": 0,
6 "previous": "0000014735eeda35fd8c2e303ceda4ff8fd5c67fbb032187c75eeb319daec123",
7 "transaction_mroot": "0000000000000000000000000000000000000000000000000000000000000000",
8 "action_mroot": "0000000000000000000000000000000000000000000000000000000000000000",
9 "schedule_version": 0,
10 "header_extensions": [],
11 "producer_signature": "SIG_K1_111111111111111111111111111111111111111111111111111111111111111116uk5ne"
12 }
13//构建默克尔树之后
14"header": {
15 "timestamp": "2018-10-10T12:32:30.500",
16 "producer": "eosio",
17 "confirmed": 0,
18 "previous": "0000014735eeda35fd8c2e303ceda4ff8fd5c67fbb032187c75eeb319daec123",
19 "transaction_mroot": "12399917b8b8a3d7eb05aa58dd87aec2bbbda139e770627332da9e6f5efd7d88",
20 "action_mroot": "2b4c51c20fb35268628e8f2c5171549fa5bcb947079ed82a7f2d38c7481f8c4e",
21 "schedule_version": 0,
22 "header_extensions": [],
23 "producer_signature": "SIG_K1_111111111111111111111111111111111111111111111111111111111111111116uk5ne"
24 }
通过对比可以发现transaction_mroot及action_mroot发生了相应的变化,至此eos中构建默克尔树的流程也已经完成。
本文简单的介绍了默克尔树的基本概念,以《笑傲江湖》华山派为例介绍默克尔树的构建,以及eos中transaction和action的默克尔树的构建,关于默克尔树在eos中的具体使用,我们慢慢再谈。
如果你觉得我的文章对你有一定的帮助,请点击文章末尾的喜欢该作者。
如果你对eos开发感兴趣,欢迎关注本公众号,一起学习eos开发。
微信公众号
有任何疑问或者指教请添加本人个人微信,当然有对eos开发感兴趣或者金庸粉的也可以添加一起交流,备注eos开发或金庸。
个人微信号