人工智能通识-编程-图灵机之停机问题

欢迎关注我的专栏( つ•̀ω•́)つ【人工智能通识】

之前的文章人工智能通识-科普-图灵机之繁忙的海狸Busy beaver主要涉及了三个问题：可计算性问题、停机问题和计算的复杂度问题。

停机问题 Halting Problem

停机问题是指我们让计算机启动一段代码程序，依照程序进行运算，比如图灵机根据卡片或表格规则反复读写和移动，如果计算机能够完成这个计算流程并且最后自己停下来，那么我们就认为这个程序正常，不会遇到停机问题。——换句话说，如果它自己运行起来就停不下，那就是遇到了停机问题。

在繁忙的海狸游戏中我们设定0状态为停机状态，假如卡片上的全部规则都不跳转到0状态，那么肯定就不会停机。——或者虽然某些条规则会转到0状态，但是这个规则永远也不会被用到，那么也不会停机。

比如最简单的一张卡片状态1，如果规定无论读取到1或者0，都往左走一格，然后还跳转到这个状态1，那么就是死循环，不能结束，遇到了停机问题。

在繁忙的海狸中，3个状态卡片的情况就有1600多万中可能的走法，哪些会停机？哪些不会？这怎么判断呢？

当时我们说这是无法判断的，严谨地说，应该是我们无法判定所有程序是否停机，因为有很多明显的停机情况很容易找到规律或给出证明。

为什么我们不能让计算机自己判断每个走法是否能停机？——而不是直接去尝试那些走法才浪费时间？

因为这是不可能的，图灵在20世纪30年代就证明这是不可能的。

要推翻一个假设，最好的办法就是假设它是成立的，沿着这个假设继续推理，如果推理出矛盾，那么就证明这个假设是不靠谱的。

假设我们有一个方盒机器，我们向他输入一个程序代码a，它就能输出是或者否，以此表示我们输入的程序是否会自动停机。

我们不管这个方盒机器怎么运行的，它就是个图灵假想的黑盒，它符合我们能够判定所有程序是否停机的假设。沿着这个假设思考下去。

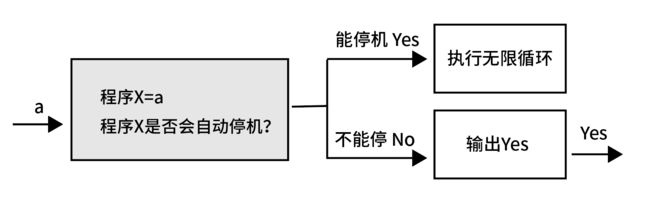
假设我们有一个程序如下所示，它包含了一个图灵判定黑盒，这个黑盒当然可以正确判定输入的a是否能够停机（依照假设前提成立），当a能自动停机时候就输出yes，不能停就输出No。

但是我们在这个黑盒后面又加了一个两个白盒。如果前面的小黑盒输出Yes，那么就进入一个无限循环白盒，如果前面输出No那么就直接输出Yes。

如果我们把上面这个程序当成一个要被判定是否停机的程序，整个打包作为一个程序放入到大的黑盒里面去，就是下图中蓝色范围部分。这时候会发生什么？

如果a能够停机，那么大黑盒就输出Yes。但是如果a能停机，那么小黑盒也输出Yes然后进入无限循环，也就是说这时候蓝盒不能停机。这就产生了矛盾，到底能停不能停？

相反的，如果a不能停机，那么大黑盒应该输出No，但实际上小黑盒会进入Yes白盒，输出Yes，这又是矛盾。

如果外层是肯定的，那么内层就会是否定的；如果外层是否定的，那么内层就会是肯定的。这个矛盾是无法调和的。

所以，至少在这个情况下，一个机器不能正确判断自身运行的程序是否会停机。即一个机器对自身运行的所有程序是否停机做出正确判断。

这是一个循环嵌套的情况，计算机无法对这种嵌套的情况作出正确判断，不只是计算机，人也做不到，或者说任何系统都没法处理这样的情况。下一篇我们来一起看发生在人身上的类似问题。

欢迎关注我的专栏( つ•̀ω•́)つ【人工智能通识】

如果您发现文章错误，请不吝留言指正；
如果您觉得有用，请点喜欢；
如果您觉得很有用，欢迎转载~

END