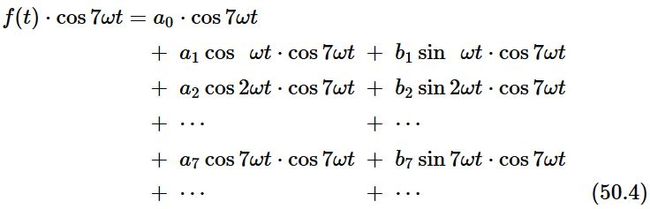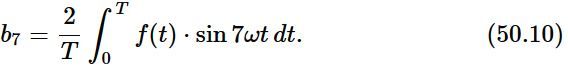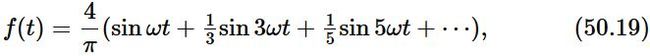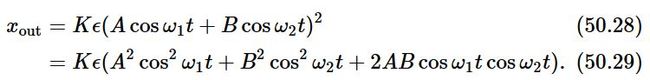content
- Pythagoras' Interesting Discovery
- Noise and music
- Fourier Series
- Motion of a string
- Motion of the air -- the pressure
- Quality and consonace
- The Fourier coefficients
- The energy theorem
- Nonlinear responses
- PS
0 Pythagoras' Interesting Discovery
Pythagoras is said to have discovered the fact that two similar strings under the same tension and differing only in length, when sounded together give an effect that is pleasant to the ear if the lengths of the strings are in the ratio of two small integers. If the lengths are as one is to two, they then correspond to the octave in music. If the lengths are as two is to three, they correspond to the interval between C and G, which is called a fifth. These intervals are generally accepted as “pleasant” sounding chords.
“天籁之音”震惊毕达哥拉斯,毕达哥拉斯学派以此为基而创立。
They held mysitc beliefs in the great powers of numbers.
The music of the spheres:
The idea was that there would be some numerical relationships between the orbits of the planets or between other things in nature.
自然界中的确存在 a simple numerical relationship,这个世界简单、复杂、奇妙、有趣。
It must have been very surprising to suddenly discover that there was a fact of nature that involved a simple numerical relationship.
This discovery led to the extension that perhaps a good tool for understanding nature would be arithmetic and mathematical analysis.
你看,理解这个世界,我们还需要数学分析吧。继续探索吧,少年。Keep moving。
我们发现:
the discovery had to do with two notes(音符) that sound pleasant to the ear.
那我们不禁要问啦:
why only certain sounds are pleasant to our ear?
对啊!为什么呢?那我们就来听听 Feynman 如何说吧。
In this one discovery of the Greeks, there are the three aspects:
- experiment,
- mathematical relationships, and
- aesthetics.
Physics has made great progress on only the first two parts. This chapter will deal with our present-day understanding of the discovery of Pythagoras.
1 Noise and Music
我们听到的声音中,有一种就是噪音。你看,生活中存在这很多的噪音。那什么是噪音?
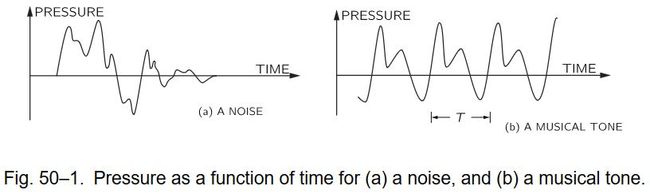
Noise corresponds to a sort of irregular vibration of the eardrum that is produced by the irregular vibration of some object in the neighborhood.
通过鼓膜上的压力变化(物体振动-空气振动-耳膜上的压力),我们观察一下噪音。
the pressure of the air on the eardrum (therefore, the displacement of the drum):
而音乐就不同,它由美妙的旋律所构成。
Music is characterized by the presence of more-or-less sustained tones—or musical “notes.”
(Musical instruments may make noises as well!)
那么,from the point of view of the pressure in the air,音符有什么特征呢?和噪音又有什么区别呢?
- 【周期性】Fig. 50-1(b) vs 【杂乱无章】 Fig. 50-1(a) (pressure varies with time)
- A musical note differs from a noise in that there is a periodicity in its graph.
- There is some uneven shape to the variation of the air pressure with time, and the shape repeats itself over and over again.
上面是从空气压力的角度来看音符和噪音。
音乐家们看音符就不同啦,他们从3个方面观察音符:
- the loudness :corresponds to the maginitude of the pressure changes. 压力变化幅值大小
- the pitch : corresponds to the period of time for one repetition of the basic pressure function. 时间上的周期
- “Low” notes have longer periods than “high” notes.
- 低音符的repetition周期T长,对应的频率1/T就小,所以就低音了嘛
- the “quality” of a tone has to do with the differences we may still be able to hear between two notes of the same loudness and pitch.
An oboe(双簧管), a violin, or a soprano(女高音) are still distinguishable even when they sound notes of the same pitch. The quality has to do with the structure of the repeating pattern.
这里 the structure of the repeating pattern 具体指的的什么呢? what pattern?what's the difference between these patterns.
so 音符质量就看得个人的音乐修养。
我们做个试验吧。上面的独弦琴上就一根弦,你弹一下它,它就振动,再通过空气振动传到我们的耳朵里,我们就听到声音。
有时间自己也玩玩吧,用吉他也是可以的呢。
下面我们来分析
why a plucked string produces a musical tone.
2 The Fourier Series
我们这一趟旅行来到的是 Joseph Fourier 先生 21 March 1768 – 16 May 1830 最先研究的 Fourier Series.
Motion of a string
一根弦的自由振动有好多的 normal modes. 这个我们在 vibrations and waves 看到过一根弦的振动方程。
We have seen that a string has various natural modes of oscillation, and that any particular kind of vibration that may be set up by the starting conditions can be thought of as a combination—in suitable proportions—of several of the natural modes, oscillating together.
弦实际的振动就是这些 normal mode 叠加的结果。
For a string we found that the normal modes of oscillation had the frequencies ω0, 2ω0, 3ω0, …
所以说,弦的一般运动方程是以基频w0和其倍频所组成的简谐方程(运动)的叠加。
- 1st normal mode, T1 = 2π/(w0);
- 2nd normal mode, T2 = 2π/(2w0) = (T1)/2
- 3rd ... T3 = 1/3*T1
Motion of the air --- the sound
We have been talking about the motion of the string. But the sound, which is the motion of the air, is produced by the motion of the string, so its vibrations too must be composed of the same harmonics---though we are no longer thinking about the normal modes of the air.
Also, the relative strength of the harmonics may be different in the air than in the string, particularly if the string is “coupled” to the air via a sounding board. The efficiency of the coupling to the air is different for different harmonics.
我们知道 a string 的振动其实是由其normal mode 叠加而成。那么,我们要看看 the motion of the air. 空气的运动是由弦的运动造成的。 看空气的运动,我们就观察 the air pressure.
Let f(t) represent the air pressure as a function of time for a musical tone. [类似图Fig.50-1(b)所显示]
那么按 弦 的运动方程,我们希望 f(t) 也可以写成一系列 SHF(simple harmonic functions)的和,如coswt 一些列简谐波的叠加,其他的频率就是2w, 3w, etc.
要是有相位怎么办,不可能所有频率下的简谐波相位是一样的,这个嘛,我们就加入相位好了, 使用 cos(wt + Φ) 。因为
其中Φ为常数,那么cosΦ 也是常数,最后还是展开为 cos(wt) 和 sin(wt) 的形式。 很自然,我们就把 f(t) 做个展开.就是 fourier Series for f(t).
We conclude, then, that any function f(t) that is periodic with the period T can be written mathematically as
where ω=2π/T and the a’s and b’s are numerical constants which tell us how much of each component oscillation is present in the oscillation f(t).
a 和 b 就是各个频率对这个周期函数f(t) 的贡献值。
a0 对应的频率为0.
represents a shift of the average value (that is, the “zero” level) of the sound pressure.
(50.2) 这个式子以图像的形式来看的话,就是下图:
We have said that any periodic function can be made up in this way. We should correct that and say that any sound wave, or any function we ordinarily encounter in physics, can be made up of such a sum. The mathematicians can invent functions which cannot be made up of simple harmonic functions—for instance, a function that has a “reverse twist” so that it has two values for some values of t! We need not worry about such functions here.
好啦,到这里,我们知道任何周期性函数f(t)[sound wave] 都可以通过 Fourier Series 展开。对于非周期的,我们可以延拓成周期性的,这个就是后话啦,在这里,我们就不再展开。
3 Quality and consonace
现在我们要看看音调的质量啦。这个就要看式子(50.2)中 a 和 b 的值了。
- A tone with only the first harmonic is a “pure” tone.
- A tone with many strong harmonics is a “rich” tone.
A violin produces a different proportion of harmonics than does an oboe.
An electric organ(电风琴) works in much this way. The “keys” select the frequency of the fundamental oscillator and the “stops” are switches that control the relative proportions of the harmonics. By throwing these switches, the organ can be made to sound like a flute, or an oboe, or a violin.
It is interesting that to produce such “artificial” tones we need only one oscillator for each frequency—we do not need separate oscillators for the sine and cosine components.
只要各个基频和倍频的振荡器就可以制造 tones。
We all know that a particular vowel sound—say “e–e–e”—still “sounds like” the same vowel whether we say (or sing) it at a high or a low pitch. From the mechanism we describe, we would expect that particular frequencies are emphasized when we shape our mouth for an “e–e–e,” and that they do not change as we change the pitch of our voice. So the relation of the important harmonics to the fundamental—that is, the “quality”—changes as we change pitch. Apparently the mechanism by which we recognize speech is not based on specific harmonic relationships.
那么 如何解释最初所提到的毕达哥拉斯观察到的现象呢?
两根相同弦的长度不同:2:3.那么它们的基频比率为3:2, 可以观察公式(6-11)下面的公式得到。那为什么会听起来如此悦耳呢?我们从 the frequencies of the harmonics 来找找线索吧。
- 弦1长为 L1 = 2L0, 其 normal mode 基频和倍频为 3w0, 6w0, 9w0;
- 弦2长为 L2 = 3L0, 其 normal mode 基频和倍频为 2w0, 4w0, 6w0;
The second harmonic of the lower shorter string will have the same frequency as the third harmonic of the longer string. (It is easy to show—or to believe—that a plucked string produces strongly the several lowest harmonics.)
我们来确定一下规则:
- Notes sound consonant when they have harmonics with the same frequency.
- Notes sound dissonant if their upper harmonics have frequencies near to each other but far enough apart that there are rapid beats between the two.
but
our understanding of it is not anything more general than the statement that when they are in unison they sound good. It does not permit us to deduce anything more than the properties of concordance in music.
涉及乐理知识了,之前学的一点五线谱,现在总算是有点用场。
三大和弦:F-A-C, C-E-G, G-B-D each represent tone sequences with the frequency ratio 4:5:6.
These ratios—plus the fact that an octave (C–C′, B–B′, etc.) has the ratio 1:2—determine the whole scale for the “ideal” case, or for what is called “just intonation.”纯正声调
Keyboard instruments like the piano are not usually tuned in this manner, but a little “fudging” is done so that the frequencies are approximately correct for all possible starting tones. For this tuning, which is called “tempered,” the octave (still 1:2) is divided into 12 equal intervals for which the frequency ratio is (2)^(1/12). A fifth no longer has the frequency ratio 3/2, but 2^(7/12)=1.499【为什么是这个不怎么理解呀】, which is apparently close enough for most ears.
看来调音是一门艺术啊!
4 The Fourier Coefficients
Let us return now to the idea that any note—that is, a periodic sound—can be represented by a suitable combination of harmonics.
f(t) 可以进行 fourier series 展开,那么如何得到 一系列的系数 a, b 呢?
It is easy to make a cake from a recipe; but can we write down the recipe if we are given a cake?
哈哈,这个比喻恰当。
a0 = constant.
We have already said that it is just the average value of f(t) over one period (from t=0 to t=T).
Recalling the definition of an average, we have
那么其他 a 和 b 可以利用三角函数正交性来求解。如
其他项可以用三角函数整个周期内求积分为0,最后可得到等式右边就剩下:
We see that Fourier’s “trick” has acted like a sieve(筛子) .
来看看正交性筛子:
以指数形式(Euler)来表示:(哪里都能看见欧拉公式啊!)
We now know how to “analyze” a periodic wave into its harmonic components. The procedure is called Fourier analysis, and the separate terms are called Fourier components.
例外:
The mathematicians have shown, for a wide class of functions, in fact for all that are of interest to physicists, that if we can do the integrals we will get back f(t). There is one minor exception. If the function f(t) is discontinuous, i.e., if it jumps suddenly from one value to another, the Fourier sum will give a value at the breakpoint halfway between the upper and lower values at the discontinuity.
出现间断点的问题,这个在微积分中已经讲过。在断点处 t0 处,f(t0) = 1/2[f(t0-) + f(t0+)],左右极限值的平均值。
方波的傅里叶级数展开:
5 The energy theorem
The energy in a wave is proportional to the square of its amplitude.
for a wave of complex shape, which is expressed by EQ.50.13, the Energy in one period will be proportional to
so we can write
When we expand them, we will get all possible cross terms. Because of the orthogonal of the sin and cos functions, we can get
So if the f(t) is the square wave function, and the series is Eq. 50.19, then we get
Sum
- f(t) 的能量何其幅值的平方成正比,是因其定义而来的。
- 正交性发挥着巨大的作用啊!
6 Nonlinear responses
Finally, in the theory of harmonics there is an important phenomenon which should be remarked upon because of its practical importance—that of nonlinear effects.
世间万物,奇妙无常。
线性没那么简单,宇宙布满了非线性。
线性系统和近似线性系统的响应方程为:
1
举个简单的例子,加入系统的输入为 x_in = coswt,其响应
The output has not only a component at the fundamental frequency, that was present at the input, but also has some of its second harmonic. There has also appeared at the output a constant term K(ϵ/2), which corresponds to the shift of the average value, shown in Fig. 50–5. The process of producing a shift of the average value is called rectification.
2
if x_in=Acos(ω1 t) + Bcos(ω2 t), because of nonlinearity,
The first two terms in the parentheses of Eq. (50.29) are just those which gave the constant terms and second harmonic terms we found above. The last term is new.
Modulate: w1 is much great than w2,
低频调制高频,高頻被低频调制。从另一个角度来观察下:
We have two different, but equivalent, ways of looking at the same result. In the special case that ω1≫ω2, we can relate these two different views by remarking that since (ω1+ω2) and (ω1−ω2) are near to each other we would expect to observe beats between them. But these beats have just the effect of modulating the amplitude of the average frequency ω1 by one-half the difference frequency 2ω2. We see, then, why the two descriptions are equivalent.
In summary, we have found that a nonlinear response produces several effects:
- rectification,
- generation of harmonics, and
- modulation, or the generation of components with sum and difference frequencies.
实际应用:
- 其实我们的耳朵是非线性的,那么我们听到 pure tone,经过我们的耳朵,we hear harmonics and also sum and difference frequencies
- amplifiers, loudspeakers, etc. the sound reproducing equipment always have some nonlinearity.
- modulator 调制 (解调): 非线性还是必要的。
Nonlinearities are quite necessary, and are, in fact, intentionally made large in certain parts of radio transmitting and receiving equipment.
7 PS
我们听到的,可以不是最原始的,我们耳朵存在非线性,那么我们大脑的非线性有如何呢?
- input: 所看 所听
- system:我们的大脑, nonlinear or linear, depend your way of thinking
- ouput: depended by our brain, mind, thinking etc.
The world is so beautiful, the physics behind our world or galaxy is so marvelous. Keep learning, thinking, and outputing.
Enjoy your short journey in this galaxy created by Holy God, and enjoy your life.
reference:
- Feynman R P, Leighton R B, Sands M, et al. The Feynman lectures on physics.[M]// The Feynman lectures on physics. Addison-Wesley Pub. Co. 1963:750-752.
- French A P. Vibrations and waves[M]. CRC press, 1971.
time log
All above is the note of The Feynman lectures on physics.
@安然Anifacc
2016-12-29 0-4 part added
2016-12-30 5-7 part added