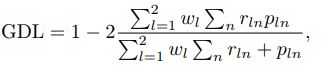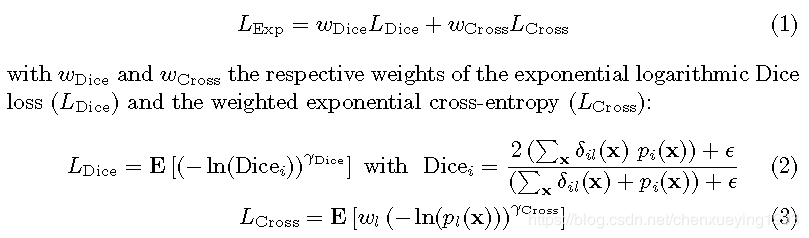3D Segmentation with Exponential Logarithmic Loss for Highly Unbalanced Object Sizes
3D Segmentation with Exponential Logarithmic Loss for Highly Unbalanced Object Sizes
现有大多数的网路只能处理相对较少数量的标签（<10）,并且在处理高度不平衡的object尺寸方面的工作非常有限，尤其是在3D分割中。在本文中，我们提出了一种网络架构和相应的损失函数，它们可以改善非常小的结构的分割。
1 Introduction
针对高度不平衡的labels，仅有很少的框架被提出。
[8] 提出一个2D网络，label weights仅被用于 the weighted cross-entropy 而不是 the Dice loss，针对3D分割堆叠2D的结果可能导致连续切片之间的不一致性。
[9] 将泛化的Dice loss作为loss function。 不是计算每个标签的Dice损失，而是针对广义Dice损失计算目标在the ground-truth and predicted probabilities之和之间的加权和上的加权和，其中权重与标签频率成反比。
当选择GDLv加权时，每个标签的贡献通过其体积的倒数进行校正，从而减少区域大小与Dice评分之间众所周知的相关性(region size and Dice score)
实际上，Dice系数对小结构是不利的，因为一些像素的错误分类会导致系数的大幅下降，并且这种灵敏度与结构之间的相对大小无关。 因此，通过标签频率进行平衡对于Dice损失是非最优的。
为了解决三维分割中高度不平衡的物体尺寸和计算效率的问题，我们在本文中有两个关键的贡献：
-
提出指数对数损失函数（the exponential logarithmic loss function.）
为了处理两类图像分类问题的高度不平衡的数据集，仅通过网络输出的softmax概率计算的调制因子乘以加权的交叉熵以关注不太准确的类。
-
提出了一种快速收敛和计算有效的网络架构，它结合了skip connections and deep supervision的优点，它只有V-Net的1/14的参数量，并且速度是V-Net的两倍。
在具有20个高度不平衡标签的脑磁共振（MR）图像上进行实验。 结合这两项创新，平均Dice系数达到82％，平均分割时间为0.4秒。
2 Methodology
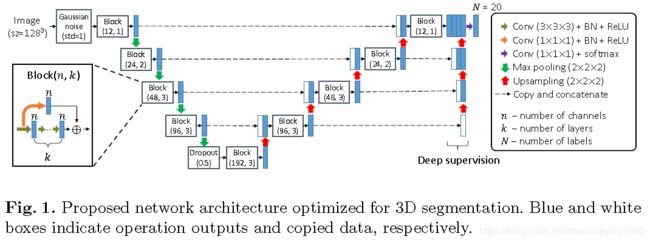
2.1 Proposed Network Architecture
The network is composed of convolutional blocks, each comprises k cascading 3_3_3 convolutional layers of n channels associated with batch normalization (BN) and recti ed linear units (ReLU).
Gaussian noise layer and a dropout layer to avoid overfitting.
we utilize deep supervision which allows more direct back-propagation to the hidden layers for faster convergence and better accuracy.
2.2 Exponential Logarithmic Loss
E[*] is the mean value with respect to i and x in LDice and LCross, respectively.
with fk the frequency of label k, is the label weight for reducing the inuences of more frequently seen labels. Dice and Cross further control the nonlinearities of the loss functions, and we use
here for simplicity.
3 Experiments
3.1 Data and Experimental Setups
Table 1(a) shows that the labels were highly unbalanced. The background occupied 93.5% of an image on average. Without the background, the relative sizes of the smallest and largest structures were 0.07% and 50.24%, respectively, thus a ratio of 0.14%.
For LExp, we set wDice = 0.8 and wCross = 0.2 as they provided the best results.
对于数据集：70% for training，30% for validation
3.2 Results and Discussion
Table 1(b) shows the Dice coeffcients averaged from the five experiments.
-
The linear
表现最差。相对较大的结构表现较好，但性能随结构尺寸的增大而降低。相反，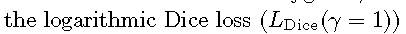
取得了更好的结果，the weighted cross entropy (LCross( =1)), whose performance was better than the linear Dice loss but worse than the logarithmic Dice loss. The weighted sum of the logarithmic Dice loss and weighted cross-entropy (LExp( = 1)) outperformed the individual losses, 取得第二好的性能。 -
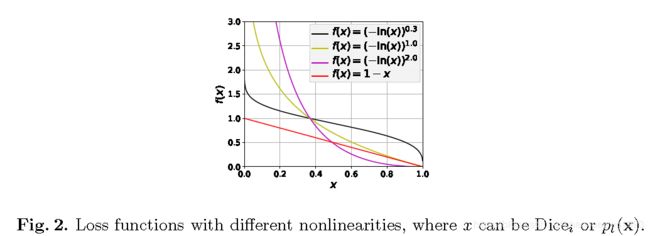
对于大的结构是无效的，这与Fig.2的观察是一致的，当精度越高时损失函数会被过度抑制。相比之下，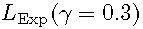
取得了最好的结果，尽管它只比
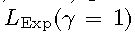略优一点，也就是说，越小的标准差说明它越精确。 -
当V-Net应用最佳的损失函数时，其性能仅好于使用Dice loss和
。这表明我们提出的网络在这个问题上比V-Net性能好。
Fig. 3 shows the validation Dice coefficients vs. epoch, averaged from the five experiments.
about 80 epochs.
更加波动。The linear Dice loss also converged at about 80 epochs but with a much smaller Dice coe_cient. Comparing between the V-Net and the proposed network with 
, the V-Net had worse convergence especially at the earlier epochs. This shows that the proposed network had better convergence.