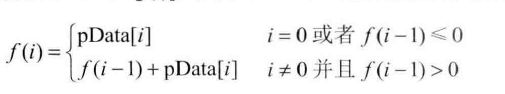LeetCode笔记——53最大子序和&剑指42

题目：给定一个整数数组 nums ，找到一个具有最大和的连续子数组（子数组最少包含一个元素），返回其最大和。

示例:

输入: [-2,1,-3,4,-1,2,1,-5,4],
输出: 6
解释: 连续子数组 [4,-1,2,1] 的和最大，为 6。

进阶:

如果你已经实现复杂度为 O(n) 的解法，尝试使用更为精妙的分治法求解。

该题属于一个最大连续子序列问题：输入是具有n各浮点数的向量x，输出是输入向量的任何连续子向量的最大和。

这个题是剑指中的42题，剑指中的思路是使用动态规划法，如果用函数f(i)表示以第i个数字结尾的子数组是最大和，那么我们需要求出max[f(i)]，其中0<=i

这个公式的意义是，当第i-1个数字结尾的子数组中所有数字的和小于0时，如果把这个负数与第i个数字相加，则得到的结果比第i个数字本身还要小，所以这种情况下第i个数字结尾的子数组就是这个数字本身；如果所有数字和大于0，则与第i个数字累加得到的就是以第i个数字结尾的子数组中所有数字的和。这种思路和下面这种算法的思路是一样的，代码如下：

public int FindGreatestSumOfSubArray(int[] array) {
if (array == null || array.length == 0)
return 0;
int cur = array[0];  //表示以i结尾的子数组中的最大和
int greast = array[0];
for (int i = 1; i < array.length; i++) {
if (cur < 0) { //最大和为负数
cur = array[i];
}else {
cur += array[i];

}
if (cur > greast) {
greast = cur;
}
}
return greast;
}

在网上有以下几种解法，在这进行一个总结：

一 扫描算法（动态规划）

这是属于一个动态规划问题。从头到尾扫描数组，扫描到sums[i]时，最大的连续子序列和要么是前i-1个的最大连续子序列和，要么是以nums[i]为结尾的最大序列和。如果以dp[i]表示已nums[i]为结尾的最大子序列和，则有以下公式：

dp[i]=max(dp[i-1]+nums[i],nums[i])

以下是代码的实现：

class Solution {
    public int maxSubArray(int[] nums) {
            //vectordp(nums.size());
        int[]dp=new int[nums.length];
        int result = nums[0];
        dp[0]=nums[0];
        for (int i = 1; i < nums.length; i++)
        {
            //dp[i] = Math.max(dp[i - 1] + nums[i], nums[i]);
            if((dp[i - 1] + nums[i])>=nums[i])
               dp[i] = dp[i - 1] + nums[i];
               else dp[i]=nums[i];
            if (result < dp[i])
                result = dp[i];
        }
        return result;
}
}

虽然挺简单，但是我自己写最后还是出错了。。。。这个题的数组中是存在负数的，所以最后在比较的时候，dp[i]表示以i为节点的最大子序和。因为dp[i-1]可能为负数，所以当其为负数时，dp[i]就为nums[i];否则dp[i]的值就可能是dp[i-1]+nums[i].除此之外我自己还把返回值写错了，dp[nums.lengh-1]表示以nums[i-1]结尾的字符串的最大子序和，但这个和并不一定是最大的，所以应该直接返回max.

二 直接解法

就是直接遍历所有可能的连续子序列，求出最大的子序列和。

以下是网上大神们的代码：

int max_array_v2_1(int *array,int length)
{
    int sum,maxsofar = NI;
    int i,j;
    for(i=0;i

依靠首尾两个变量i,j表示一个子向量，同时j增长时，可以直接使用上一次的计算和与新增元素相加

 

三  分治算法

在题目中还提到了分治算法，因此将分治算法的补充在这里。

分治法的基本思想是，把n个元素的向量分成两个n/2的子向量，递归地解决问题再把答案合并。

以下是大神们的代码：

int max_array_v3(int *array,int l,int u)
{
    int i,m;
    int lmax,rmax,sum;
    lmax = rmax = NI;
    if(l>u)
        return 0;
    else if(l == u)
        return maxnum(NI,array[l]);
    m = (l+u)/2;
    sum = 0;
    for(i=m;i>=1;i--) {
        sum += array[i];
        lmax = maxnum(sum,lmax);
    }
    sum = 0;
    for(i=m+1;i<=u;i++) {
        sum += array[i];
        rmax = maxnum(sum,rmax);
    }
    return maxnum(lmax+rmax,maxnum(max_array_v3(array,l,m),max_array_v3(array,m+1,u)));

链接地址：[珠玑之椟]字符串和序列：左移、哈希、最长重复子序列的后缀数组解法、最大连续子序列