吴恩达机器学习练习5——正则化线性回归和偏差/方差

正则化线性回归

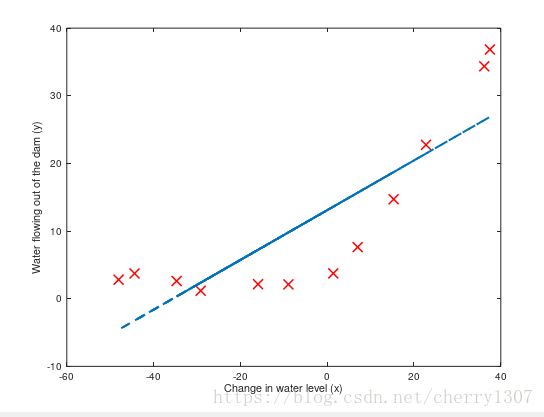
利用水库水位的变化从大坝流出的水量

数据可视化

代价函数

function [J, grad] = linearRegCostFunction(X, y, theta, lambda)
		m = length(y); % number of training examples
		J = 0;
		grad = zeros(size(theta));
		h = X*theta;
		J = (1/(2*m))*sum((h-y).^2)+lambda/(2*m)*sum(theta(2:end).^2);
		temp = theta;
		temp(1) = 0;
		grad = (1/m)*X'*(h-y) + lambda/m*temp; 
		grad = grad(:);
end

拟合

偏差、方差折中

function [error_train, error_val] = ...
    learningCurve(X, y, Xval, yval, lambda)
	m = size(X, 1);
	error_train = zeros(m, 1);
	error_val   = zeros(m, 1);
	for i = 1:m
	    theta = trainLinearReg(X(1:i, :), y(1:i), lambda);
		error_train(i) = linearRegCostFunction(X(1:i, :), y(1:i), theta, 0);
		error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end

多项式回归

线性模型的问题是它对于数据来说太简单了，并导致高偏差。

即：

function [X_poly] = polyFeatures(X, p)
	X_poly = zeros(numel(X), p);
	for i = 1 : p	
		X_poly(:,i) = X.^p;
end

matlab语法
n = numel（A）；
n= numel（A，条件）；
返回数组A中元素个数。若是一幅图像，则numel(A)将给出它的像素数

特征归一化

function [X_norm, mu, sigma] = featureNormalize(X)
	mu = mean(X);
	X_norm = bsxfun(@minus, X, mu);
	sigma = std(X_norm);
	X_norm = bsxfun(@rdivide, X_norm, sigma);
end

matlab语法
bsxfun(fun,A,B)：
两个数组间元素逐个计算，fun是函数句柄或者m文件，也可以为如下内置函数 ：
@plus 加 ；         @minus 减 ；         @times 数组乘 ；         @rdivide 左除 ；        @ldivide 右除 。

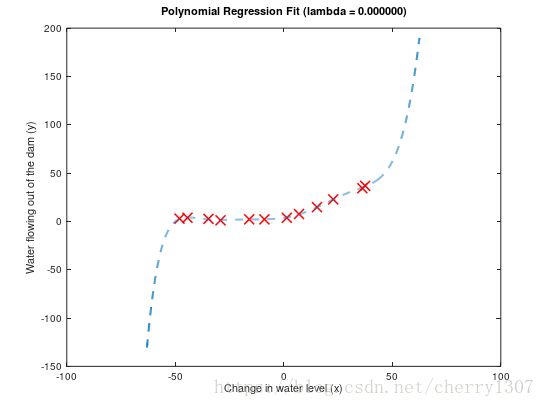
上图可以看出，训练误差小，但验证集误差大————过拟合

正则化

为验证集选择lambda

function [lambda_vec, error_train, error_val] = ...
    validationCurve(X, y, Xval, yval)
	lambda_vec = [0 0.001 0.003 0.01 0.03 0.1 0.3 1 3 10]';
	error_train = zeros(length(lambda_vec), 1);
	error_val = zeros(length(lambda_vec), 1);
	for i = 1 : length(lambda_vec)
		lambda = lambda_vec(i);
		[theta] = trainLinearReg(X, y, lambda);
		error_train(i) = linearRegCostFunction(X, y, theta, 0);
		error_val(i) = linearRegCostFunction(Xval, yval, theta, 0);
end

matlab之numel()函数
matlab之bsxfun()函数