机器学习方法篇(14)------SVM公式推导
● 每周一言
找准自己的定位,才能找到自己的快乐。
导语
前两节讲完了拉格朗日乘子法和KKT条件,而SVM正好符合拉格朗日乘子法定义的不等式约束优化问题形式,本节就基于KKT条件来推导一下SVM。
SVM公式推导
我们先回忆一下前面第11节讲到的SVM模型公式:

根据上一节讲的KKT条件,将上述SVM的公式条件先转化为小于等于形式,然后带入拉格朗日公式如下:
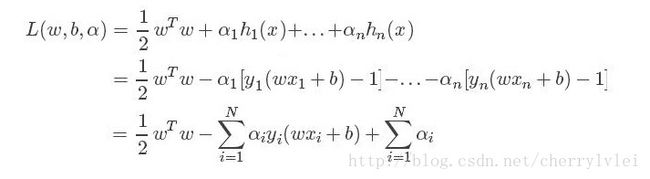
其中(xi,yi)表示第i个样本。由于我们是要求上述拉格朗日公式关于参数w和b的最小值,因此先假定αi为常数,L对w和b求导置0得:
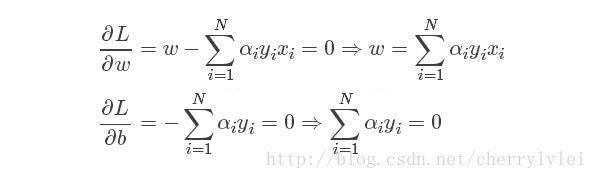
将求得的w和b的极值带回拉格朗日公式,可以消掉w和b,剩下的就是一个关于α的式子,公式推导如下:

根据拉格朗日对偶问题的定义,到了这一步就应该求W关于α的最大值问题了。这个问题可以这样直观理解,因为KKT条件中h(x)是非正函数,而α ≥ 0,如果W要求的这个极值是最小值,那么无穷大的α会使W的值变得无穷小。因此,我们得到了SVM的“半成品”公式:
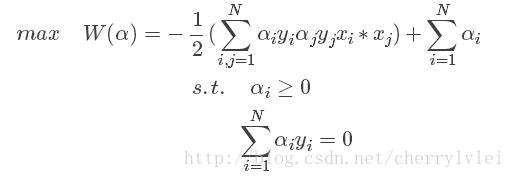
之所以是“半成品”,是因为到目前为止,我们基于的都是样本完全线性可分的条件。而实际情况往往正负样本之间都会夹杂噪声,即正样本区域包含少量负样本,而负样本区域包含少量正样本。这个时候就需要一个与分界面的容错距离ϵ,将这个ϵ加入到原始的SVM公式我们得到:

常数C代表了样本容错距离之和对模型最终准确率的影响程度。将上述公式中新增的部分一起带入拉格朗日公式如下:

重新L分别对w、b以及ϵ求导置0得:
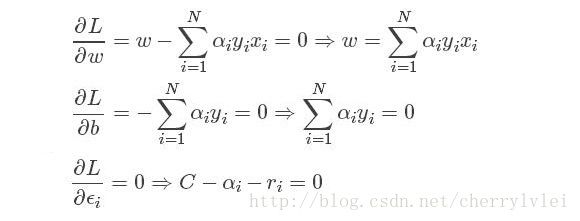
由于拉格朗日参数ri ≥ 0,所以C ≥ αi ≥ 0。然后将上述极值带回拉格朗日公式,可以消除w、b、ϵ和r,得到W关于α的最终版SVM公式如下:
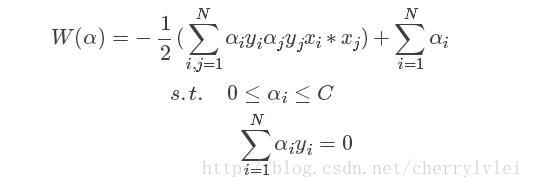
现在的目标就是寻找一组αi的最优解,使得W的值最大。而求最优解的方法叫做 SMO算法,有兴趣的读者可以自行查阅资料学习。
以上便是SVM公式的推导过程,敬请期待下节内容。
本文推导参考:http://blog.csdn.net/on2way/article/details/47729419
结语
感谢各位的耐心阅读,后续文章于每周日奉上,敬请期待。欢迎大家关注小斗公众号 对半独白!
