用Python实现八大排序算法--堆排序
一、堆排序概述
1.堆是一种数据结构
可以将堆看作一棵完全二叉树,这棵二叉树满足,任何一个非叶节点的值都不大于(或不小于)其左右孩子节点的值。

2.堆的存储
一般用数组来表示堆,若根节点存在于序号0处,i结点的父结点下表就为(i-1)/2,i结点的左右子结点下标分别为2i+1和2i+2
3.堆排序思想
利用大顶堆(小顶堆)堆顶记录的是最大关键字(最小关键字)这一特性,使得每次从无序中选择最大记录(最小记录)变得简单。
4.堆排序的实现
堆排序需要解决两个问题:
- 如何由一个无序序列建成一个堆
- 如何在输出堆顶元素之后,调整剩余元素成为一个新的堆?
针对第二个问题:一般在输出堆顶元素之后,视为将这个元素排除,然后用表中最后一个元素填补它的位置,自上向下进行调整:首先将堆顶元素和它的左右子树的根结点进行比较,把最小的元素交换到堆顶;然后顺着被破坏的路径一路调整下去,直至叶子结点,就得到新的堆。
Step 1: 构造初始堆
初始化堆时是对所有的非叶子结点进行筛选
最后一个非终端元素的下标是[n/2]向下取整,所以筛选只需要从第[n/2]向下取整个元素开始,从后往前进行调整。
Step 2:进行堆排序
堆排序是一种选择排序。建立的初始堆为初始的无序区。
排序开始,首先输出堆顶元素(因为它是最值),将堆顶元素和最后一个元素交换,这样,第n个位置(即最后一个位置)作为有序区,前n-1个位置仍是无序区,对无序区进行调整,得到堆之后,再交换堆顶和最后一个元素,这样有序区长度变为2。。。
不断进行此操作,将剩下的元素重新调整为堆,然后输出堆顶元素到有序区。每次交换都导致无序区-1,有序区+1。不断重复此过程直到有序区长度增长为n-1,排序完成。
5.堆排序实例
1)首先,建立初始的堆结构图
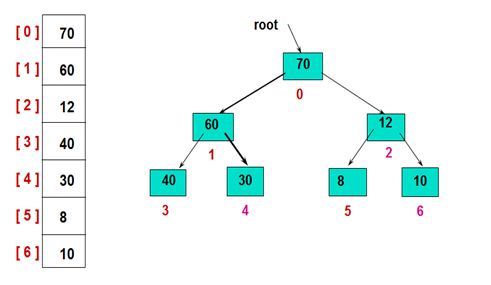
2)然后,交换堆顶的元素和最后一个元素,此时最后一个位置作为有序区(有序区显示为黄色),然后进行其他无序区的堆调整,重新得到大顶堆后,交换堆顶和倒数第二个元素的位置……
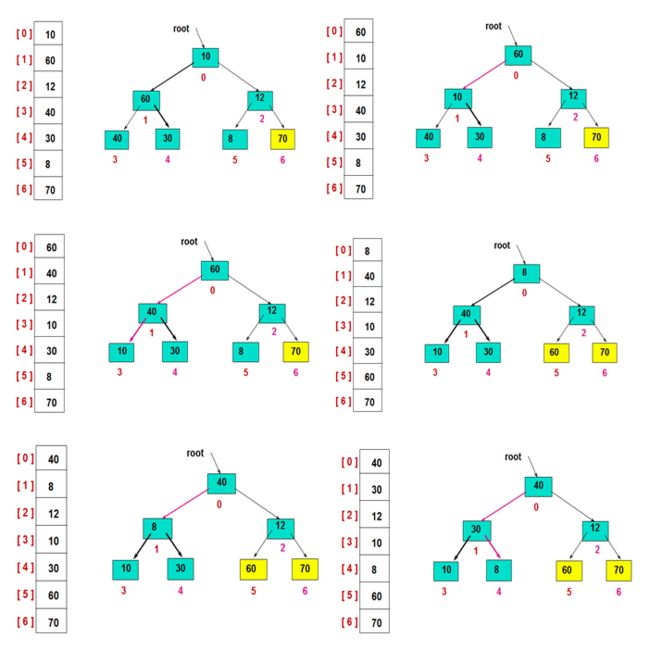
3)重复此过程
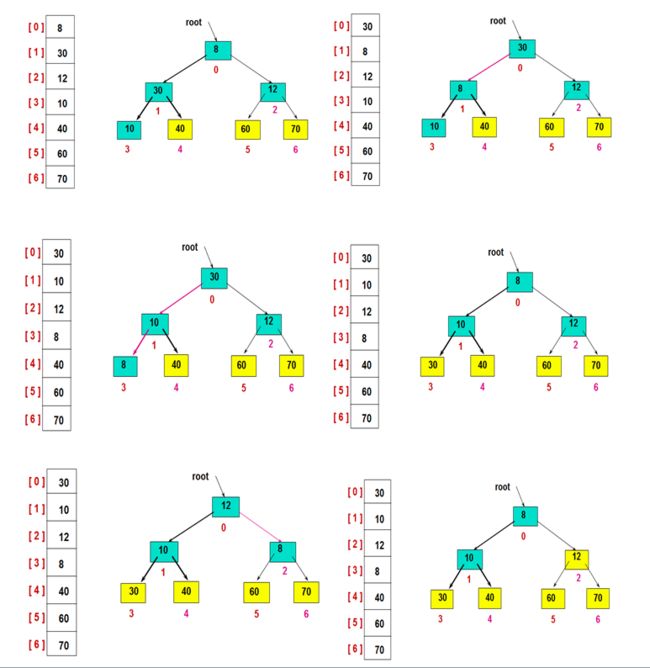
4)最后,有序区扩展完成即排序完成

由排序过程可见,若想得到升序,则建立大顶堆,若想得到降序,则建立小顶堆。
6.堆排序分析
稳定性:
时间复杂度:O(nlogn)
空间复杂度:
堆排序方法对记录数较少的文件并不值得提倡,但对n较大的文件还是很有效的。因为其运行时间主要耗费在建初始堆和调整建新堆时进行的反复“筛选”上。