易解AVL - AVL的插入及插入调整
什么时AVL树?
在数据结构中,AVL树是最先发明的自平衡二叉查找树。在AVL树中任何节点的两个子树的高度差的绝对值不能超过一,所以它也被称为高度平衡树。查找、插入和删除在平均和最坏情况下都是O(log n)。增加和删除可能需要通过一次或多次旋转来使得AVL树保持平衡。
AVL树的本质是一棵二叉搜索树,它的特性是:
解释:
节点的平衡因子是它的左子树的高度减去它的右子树的高度。平衡因子可以直接存储在每个节点中,带有平衡因子 1、0 或 -1 的节点被认为是平衡的。带有平衡因子 -2 或 2 的节点被认为是不平衡的,并需要重新平衡这个树。
图解:
构建平衡二叉树的插入操作可能会引起的四种不平衡的情况。
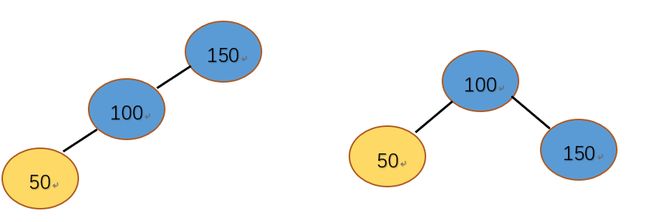
情况一:在待插入结点50插入之前,100平衡因子=0 , 150平衡因子=1 。在50插入后,父结点100平衡发生了变化,100左子树高度-右子树高度=1 ,100的平衡因子变为1 , 150的平衡因子变为 2 。 这时avl树不满足平衡的形态需要调整不平衡节点左子树的高度。因为50为100的左子树,左左右旋,以150为基点右旋转,变成一颗满足平衡二叉树的性质的树。这里需要注意的是我们在旋转之前需要把100和150的平衡因子变成0,转变之后刚好正确。
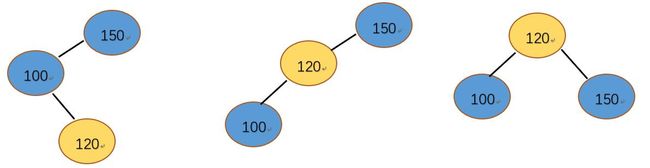
情况二:在待插入结点120插入之前,100平衡因子=0 , 150平衡因子=1 。在120插入后,父结点100平衡发生了变化,100左子树高度-右子树高度 =-1,100的平衡因子变为 -1 , 150的平衡因子变为 2 (因为对于150左子树比右子树高所以还是2)。 这时avl树不满足平衡的形态需要调整不平衡节点左子树的高度。因为120为100的右子树,左右先左旋再右旋,先以100为基点左旋转,再以150为基点右旋转。此时avl树又满足了平衡的性质,但是由于两层旋转,变化有一些多,我们在调整平衡因子的时候,把情况二分成了三种情况。
(1)第一种情况:也就是下图展示的情况,待插入结点的平衡因子为0,那么我们旋转前只需要把100和150平衡因子设置为 0 即可进行二次旋转。
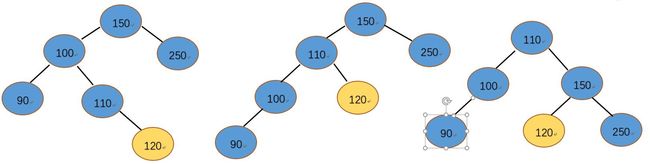
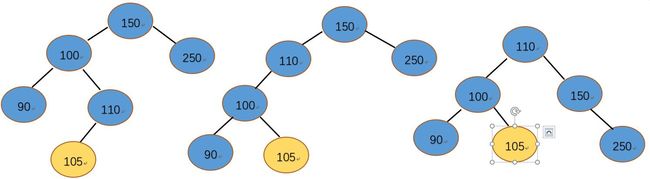
(3).情况三:待插入结点105,父结点110平衡因子为1,100平衡因子为-1 , 150平衡因子为2 ,150结点失衡左子树比右子树高2,需要重新调整。由于105经过100为基点左旋,105变成100的右子树100平衡,所以我们需要旋转前把100平衡因子设为0,150基点右旋后确实左子树,右子树比左子树高1,所以旋转前把150平衡因子设置为-1,110平衡因子设置为0。avl树恢复平衡。
至此插入操作的左失衡的所有情况都已经交代清楚了。
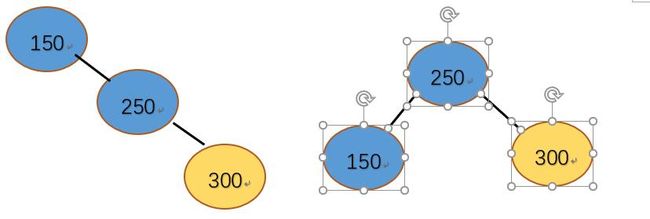
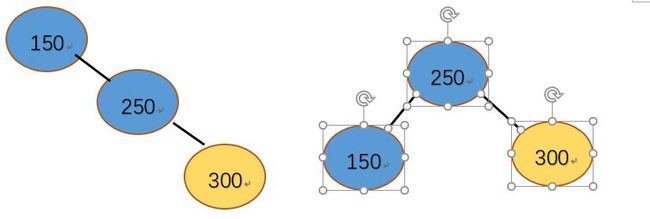
情况三:插入结点300,150平衡因子变为-2,avl树失衡,右右失衡所以我们直接可以以150为基点进行左旋转,使树满足平衡二叉树的性质。在旋转之前我们需要把150平衡因子设为0,把250平衡因子设为0.旋转过后自然平衡。
情况四:待插入结点200,父结点250平衡因子为1,150平衡因子为-2,那么此时二叉树不满足avl平衡条件,需要进行调整。因为这是一个右左的情况,所以我们需要对其先以250为基点右旋转,再以150为基点左旋转。但是又是由于有两重旋转所以调整平衡因子又多了三种情况
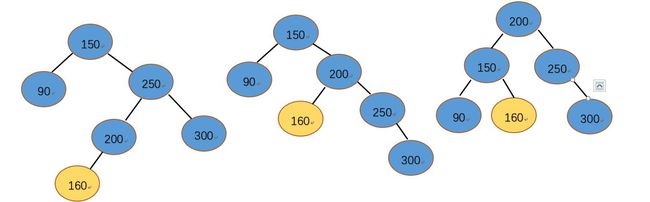
第一种情况:就是下面这种,失衡节点右孩子的左孩子平衡因子为0,那么我们在旋转之前设置250为0,150为0,旋转之后自然平衡满足平衡二叉树的性质。
第二种情况:也就是插入结点160的父结点平衡因子为1,此时150平衡因子为-2,250平衡因子为1,这种情况我们需要把250平衡因子设置为-1,把150平衡因子设置为0,200平衡因子设置为0,然后以250为基点右旋,以150为基点左旋,即可达到平衡状态。
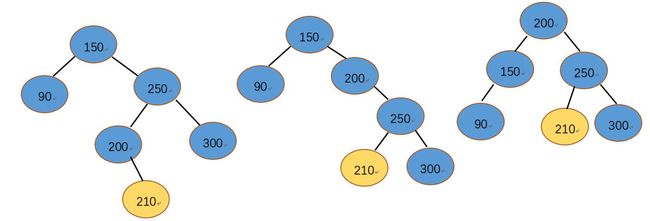
第三种情况:也就是待插入结点210的父结点200平衡因子为-1,250平衡因子为1,150结点平衡因子为-1,我们需要把150平衡因子设置为1,把250平衡因子设置为0,200平衡因子设置为0,然后以250为基点右旋,以150为基点左旋avl树平衡。
描述:我们在插入一个结点avl树平衡发生改变时候总是可能会遇到上面的几种情况,对于插入后我们需要对插入节点向上进行回溯,回溯的目的主要是检测树是否失衡,和维护树的平衡因子。当我们检测到树发生了失衡的情况,我们就会根据失衡节点判断树是发生了左失衡或右失衡,进而判断左失衡或右失衡中确定的哪种情况,然后更改平衡因子,旋转恢复平衡。这是我对avl树的插入操作大概想法。
avl树的内部数据
avl树类型定义
public class AVLTree { 成员属性:
public AVLNode treeRoot = null;
private static final int LH = 1; //左子树 - 右子树 = 1 左高
private static final int EH = 0; //左子树 - 右子树 = 0 左右子树同高
private static final int RH = -1; //左子树 - 右子树 = -1 右高
内部结点类
/**
* 静态内部类AVLNode avl树所使用的结点类
* @param
*/
private static class AVLNode{
public AVLNode lChild = null;
public AVLNode rChild = null;
public AVLNode parent = null;
public E data = null;
public Integer bf = 0;
public AVLNode(){}
public AVLNode(E data){
this.data = data;
}
public AVLNode(E data,Integer bf){
this.data = data;
this.bf = bf;
}
public AVLNode(E data, AVLNode parent){
this.data = data;
this.parent = parent;
}
}
/**
* 左旋转 以node为基点
* @param
* @return
*/
public void leftRotateChange(AVLNode node){
AVLNode temp = node.rChild;
node.rChild = temp.lChild;//node接替其右孩子的左儿子
if(temp.lChild != null) temp.lChild = node;
temp.parent = node.parent;//node右孩子变成爹
if(node.parent == null) this.treeRoot = temp;
else if(node == node.parent.lChild) node.parent.lChild = temp;
else node.parent.rChild = temp;
temp.lChild = node;//node变成左孩子
node.parent = temp;
}
/**
* 右旋转 node为基准点
* @param
* @return
*/
public void rightRotateChange(AVLNode node){//node接替左孩子的右孩子
AVLNode temp = node.lChild;
node.lChild = temp.rChild;
if(temp.rChild != null) temp.rChild = node;
temp.parent = node.parent;//右孩子变成爹
if(node.parent == null) this.treeRoot = temp;
else if(node == node.parent.lChild) node.parent.lChild = temp;
else node.parent.rChild = temp;
temp.rChild = node;//node变成右儿子
node.parent = temp;
} 插入外部调用方法
/**
* 插入值
* @param data
* @return
*/
public boolean insertAVL(E data){
try {
if(data == null) return false;
System.out.println("提示:插入的数据为:" + data + " 2秒后开始插入!");
Thread.sleep(10);
return insertAVL(new AVLNode(data));//将data包装进结点,然后拿去对比删除
} catch (InterruptedException e) {
e.printStackTrace();
return false;
}
}
/**
* 插入的方法
* 如根节点为空插入到根节点,根结点不为空,比值找位置
* 找到位置后插入,以插入的父结点开始向上回溯
* 插入的数据小 父bf + 1 否则 bf --
* 若节点的bf为0,不再向上调整BF值,
* 若bf绝对值为2 则直接上检测台
* @param node
* @return
*/
public Boolean insertAVL(AVLNode node){
AVLNode index = this.treeRoot; //用作遍历
AVLNode parent = this.treeRoot; //用作定位父结点
int cmp = 0; //用于找寻插入位置
if(this.treeRoot == null){ //如果树根是空的那就让node为根节点。结束当前方法。
this.treeRoot = node;
System.out.println("提示:树为空,已经被插入到树的根节点!");
return true;
}
//找插入点
while (index != null) { //已排除树根是空的情况 如果index遍历后为空那么index就是插入位置
parent = index;
cmp = node.data.compareTo(index.data);
if(cmp < 0){ //小于0就要去左子树中找
index = index.lChild;
}else if(cmp > 0){
index = index.rChild; //大于0就要去左子树中找
}else{
System.out.println("提示:插入的结点值与树中的重复,不必再次插入!");
return false;
}
}
node.parent = parent; //parent为index的父亲,index的位置就是node需要进行插入的位置所以我们要将node插入
if(cmp < 0){
parent.lChild = node;
System.out.println("提示:已经被插入到值为:" + parent.data + " 结点的左孩子");
}else{
parent.rChild = node;
System.out.println("提示:已经被插入到值为:" + parent.data + " 结点的右孩子");
}
//自下向上回溯,查找最近不平衡节点
while(parent!=null){
cmp = node.data.compareTo(parent.data);
if(cmp < 0){ //插入节点在parent的左子树中
parent.bf++;
}else{ //插入节点在parent的右子树中
parent.bf--;
}
if(parent.bf == 0){ //此节点的balance为0,不再向上调整BF值,且不需要旋转
break;
}
if(Math.abs(parent.bf) == 2){ //找到最小不平衡子树根节点
System.out.println("提示:发生了不平衡,值为:" + parent.data + " 结点的平衡因子值为:" + parent.bf);
insertFixedUP(parent);
break; //不用继续向上回溯
}
parent = parent.parent;
}
return true;
}
插入调整分支方法
/**
* 调整的方法:
* 1.unbalance为2时,即左子树高于右子树,leftLoseBalance(unbalance):
*
* 2.unbalance为-2时,即右子树高于左子树,rightLoseBalance(unbalance);:
*
*/
private Boolean insertFixedUP(AVLNode unbalance){
return (unbalance.bf == 2) ? leftLoseBalance(unbalance): rightLoseBalance(unbalance);
}
/**
* 左边失衡的情况
*/
public boolean leftLoseBalance(AVLNode unbalance){
System.out.println("提示:unbalance结点的左子树高于右子树。");
AVLNode unbLChild = unbalance.lChild;
if ( 1 == unbLChild.bf){
System.out.println("提示:unbalance结点的左孩子平衡因子为1,调整平衡因子,以unbalance结点为基准点右旋转");
unbalance.bf = unbLChild.bf = EH; //unbLChild平衡因子为1 直接修改 unbLChild 和unbalance值为0
rightRotateChange(unbalance);
}else if (-1 == unbLChild.bf){
System.out.println("提示:unbalance结点的左孩子unbLChild的平衡因子为-1,需要做多重考虑。");
AVLNode rd = unbLChild.rChild;
switch (rd.bf) { //调整各个节点的BF
case LH: //情况1
//rd值为1的话就是说 rd左子树高 左旋右旋转后 rd左子树会转到 unbLChild的右子树上 unbalance的右子树会比左子树高1
System.out.println("提示:情况一,unbLChild右孩子的bf值为1");
unbalance.bf = RH; //这种情况下我们修改失衡节点的bf值为-1
unbLChild.bf = EH; //修改失衡节点的左孩子的值为0
break;
case EH: //情况2
System.out.println("提示:情况二,unbLChild右孩子的bf值为0");
unbalance.bf = unbLChild.bf = EH; //rd值为0的话就是说 失衡节点没有右孩子 我们直接赋值unbalance和unbLChild为0
break;
case RH: //情况3
//rd值为-1的话就是说 rd右子树高 左旋右旋转后 rd右子树会转到 unbalance的左子树上 unbLChild左子树会比右子树高1
System.out.println("提示:情况三,unbLChild右孩子的bf值为-1");
unbalance.bf = EH; //设0
unbLChild.bf = LH; //设1
break;
}
rd.bf = EH;
leftRotateChange(unbLChild);
rightRotateChange(unbalance); }else if ( 0 == unbLChild.bf){
unbLChild.bf = RH;
unbalance.bf = LH;
rightRotateChange(unbalance);
return false;
}
return true;
}
/**
* 右边失衡的情况
*/
public boolean rightLoseBalance(AVLNode unbalance){
System.out.println("提示:unbalance结点的右子树高于左子树。");
AVLNode unbRChild = unbalance.rChild;
if( -1 == unbRChild.bf){
System.out.println("提示:unbalance结点的右孩子平衡因子为-1,调整平衡因子,以unbalance结点为基准点左旋转");
unbalance.bf = unbRChild.bf = EH;
leftRotateChange(unbalance);
}else if( 1 == unbRChild.bf){
System.out.println("提示:unbalance结点的右孩子unbLChild的平衡因子为1,需要做多重考虑。");
AVLNode ld = unbRChild.lChild;
switch (ld.bf) { //调整各个节点的BF
case LH: //情况1
System.out.println("提示:情况一,unbRChild左孩子的bf值为1");
unbalance.bf = EH;
unbRChild.bf = RH;
break;
case EH: //情况2
System.out.println("提示:情况一,unbRChild左孩子的bf值为0");
unbalance.bf = unbRChild.bf = EH;
break;
case RH: //情况3
System.out.println("提示:情况一,unbRChild左孩子的bf值为-1");
unbalance.bf = LH;
unbRChild.bf = EH;
break;
}
ld.bf = EH;
rightRotateChange(unbRChild);
leftRotateChange(unbalance);
}else if( 0 == unbRChild.bf){ //我再删除元素-在进行回溯时 找到失衡节点左子树<右子树失衡
unbRChild.bf = LH; //我们需要对失衡节点和他的的右孩子进行调整,由于左边失衡所以需要左旋转
unbalance.bf = RH; //右孩子如果本身为0,旋转过时必须先初始化为1 因为转过去左子树会嫁接到父结点的右子树上
leftRotateChange(unbalance); //因为原先为0,旋转后所以左比右高1,故如此设计。 而由于左子树本身就少1父结点左旋后右子树
return false; //变长了所以旋转前设置父结点为-1
}//删除时要考虑的情况,再看插入的时候不用细想,不影响插入
return true;
} 总结:代码已经粘贴完毕,经测试,我没有发现任何bug,如果我的想法是错的或者我的代码出现了问题,请指出我一定改,如果我的想法弄乱了您对avl树的理解,那么我在此跟您说一句对不起,我的想法一方面来自于书籍,另一方面也阅读了大量的网上大神的博客。