向量

向量在计算几何中有很大用途，下面总结一下向量常见的几种用法。

定义一个向量：
 

struct DOT
{
	int x;
	int y;
};

向量的加减法：

int jia(DOT a,DOT b)
{
	return DOT(a.x+b.x,a.y+b.y)
}

int jian(DOT a,DOT b)
{
    return DOT(a.x+b.x,a.y+b.y)
}

向量的数乘：

int cheng(DOT a,int v)
{
	return DOT(a.x*v,a.y*v);
}

向量的点积（点积=模长*投影长）：

int dot(DOT a,DOT b)
{
	return a.x*b.x+a.y*b.y;
}

可以通过点积=模长*投影长来求向量的模长与投影：

int len(DOT a)
{
	return sqrt(dot(a,a));
}

int shadow(DOT a,DOT b)
{
	return dot(a,b)/len(b);
}

向量的叉积：

int cro(DOT a,DOT b)
{
	return a.x*b.y-a.y*b.x;
}

叉积的意义就是向量a和向量b所构成的平行四边形的有向面积，注意是有正负之分的。

我们可以用向量a与向量b的叉积来判断b是在a的左手向还是右手向，左手向的叉积为正，右手向的叉积为负。

求垂直向量：

int chuizhi(DOT a)
{
	return DOT(-a.y,a.x);
}

 

以上是向量的有关操作，下面讲讲用向量表示直线与这种表示方法的有关计算。

用向量表示直线，首先我们要找到向量上的一个点，设为P(px,py)，然后求出这条直线的向量（任意两个点的坐标做差）(vx,vy)，接着我们就可以用P+λ*V来表示这条直线了。

定义如下：

struct line
{
	double px;
	double py;
	double vx;
	double vy;
};
line a[MAXL];

这种表示方法不用想斜截式那样，要分类讨论很多种情况，所以这一种方法是十分方便的。

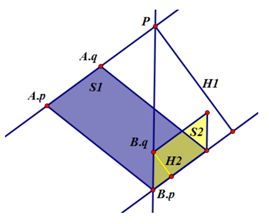
下面是求两直线的交点。求两直线的交点时我们要通过做平行和垂直，并且通过导面积来求，比较复杂，下面粘一张图：

（图片转载自某dalao的计算几何基础讲解）

我们要求A与B的向量，那么我们在A和B上分别取A.p、A.q和B.p、B.q四个点。我们要求的是BP的长度，那么就作两条垂直H1和H2，BP/B.q=H1/H2，而H1/H2就等于两个平行四边形四边形的面积比，而平行四边形的面积比有可以用叉积求出，那么我们就可以求出P点的坐标了。

贴一下代码：

int inter(int i,int j)
{
	double c1,c2,g;
	c1=cro(a[i].vx,a[i].vy,a[i].px-a[j].px,a[i].py-a[j].py);
	c2=cro(a[i].vx,a[i].vy,a[j].vx,a[j].vy);
	g=c1/c2;
	xj=a[j].px+a[j].vx*g;
	yj=a[j].py+a[j].vy*g;
}

代码中c1和c2分别表示连个平行四边形的面积。

至于点到直线的距离，可以用点积和叉积来求。

有关向量的操作我目前学到的基本上就是这些了。