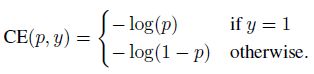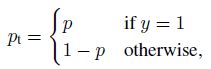Focal loss and RetinaNet
这是一篇论文阅读笔记
论文链接:https://arxiv.org/abs/1708.02002
代码链接:https://github.com/facebookresearch/Detectron
首先,提一个问题,为什么one stage方法精度比two stage方法精度低?
这个问题是本篇论文讨论与解决的主要问题.
作者总结道,一个很重要的因素是因为在one stage方法中,正负样本的不均衡。
那么one stage方法为什么正负样本就不均衡了呢?
这里举个例子:
首先来看一个典型的one stage方法,SSD。在SSD中,首先按照一定的规律产生Prior,大约会产生约10,000的候选区域,由于其实规律的采样,所以相对来说比较稠密、冗余,即使后面在分类的时候采用了hard example mining(对分数进行排序,取前面部分),但是仍然会存在较多的简单样本,使得正负样本不均衡。
相比较two stage方法,我们已Faster R-CNN为代表,在Faster R-CNN中,首先利用RPN网络产生目标框候选区域,约会生成1000-2000的候选框,这就过滤掉了大部分的简单负样本,然后在分类过程中,使用正负样本1:3或者OHEM方法使得正负样本更为均衡。
简单总结two stage的优势在于:
-
其采用两个阶段的级联,这样rpn阶段就可以将候选区域数量控制在1-2k左右,相比于one-stage要减少很多。
-
mini-batch采样,采样并不是随便采样的,而是根究正样本的位置进行采样(比如将负样本的设定为与ground-truth的IOU在0.1-0.3之间的),这样可以干掉一大部分简单样本,另外在正负样本比例上的选择,比如1:3,同样在打破平衡性。
正负样本类别不均衡带来的问题:
- 训练低效,过多的负样本,对于检测框没有作用。 (training is inefficient as most locations are easy negatives that contribute no useful learning signal)
- 过多简单的负样本会压制训练,使得训练效果不好。(enmasse the easy nagatives can overwhelm training and lead to degenerate models.)
为了解决这个问题,作者提出了Focal Loss , 并且设计了RetinaNet
一个解决正负样本的方法:Focal Loss
Focal Loss是在交叉熵损失基础上修改的,所以这里有必要先回顾一下交叉熵损失(cross entropy loss)
交叉熵损失的公式如下,这里给的是简单的Binary CrossEntropy Loss,就是只有两个类别。
简化一下,我们定义 p t p_t pt如下:
则,交叉熵损失可以表示成:
C E ( p t ) = − l o g ( p t ) CE(p_{t})=-log(p_{t}) CE(pt)=−log(pt)
当然为了更好的分析这个函数,我们将他的图像画出来,下面的图像中的蓝色的线就是该函数的曲线了,可以发现,计算是概率比较大的简单样本 p t p_{t} pt >> 0.5,依然存在一定的loss,所以当这种样本的数量较多的时候,累计起来就会比较大了,甚至会超过那些概率较小的样本(hard example),导致对于那些hard example的学习效果不佳,这也就是为什么正负样本不均衡会导致学习效果不佳,太多的简单样本,累加起来,会产生较大的影响,量变产生质变。
那么我们该如何平衡交叉熵损失呢
最简单的方法就是在交叉熵损失前面添加一个超参数,变成: C E ( p t ) = − α l o g ( p t ) CE(p_t)=-\alpha log(p_t) CE(pt)=−αlog(pt)
这样就会将这条曲线往下拉一些,使得当概率较大的时候,其影响减小。
Focal Loss Definition
借鉴了上面的方法,所以Focal Loss并没有真正改变正负样本的比例,而是修改了easy/hard example的损失权重,当然 α \alpha α取固定值当然不好,所以作者做了个自适应,完整的Focal Loss定义如下:
![]()
其中 γ \gamma γ作为调节参数,控制着缩放的比例,不同的\gamma对应的曲线,如上图figure 1所示。
Focal Loss有两个好处:
- 如果一个样本分类错误了,概率很小( p t p_t pt很小),这样相乘的系数(1- p t p_t pt)就接近于1,对样本原本的分类影响不大。
- γ \gamma γ起到了平滑的作用,作者的实验中,其等于2的效果最好。
举个例子:
取 γ \gamma γ==2,假如分类的概率是 γ \gamma γ=0.9,则原来的loss=-log(0.9) =0.046,-(1-0.9)^2 * log(0.9) = 0.00046,缩小了约100倍,加入分类概率是 γ \gamma γ=0.968,那么就会缩小约1000倍,如果概率小于0.5,如:p=0.4 , -log(0.4) == 0.39, -(1-0.4)^2 * log(0.4) = 0.14,只是减少了不到3倍。
另外,还可以增加一个参数 α \alpha α,来平衡一下倍数,如下:
这样,即使存在大量的简单样本,但是由于其带来的损失已经非常小了,所以对整体的影响也不会很大,也就不会对hard example产生较大的影响了。
基于Focal Loss 设计的 RetinaNet Detector
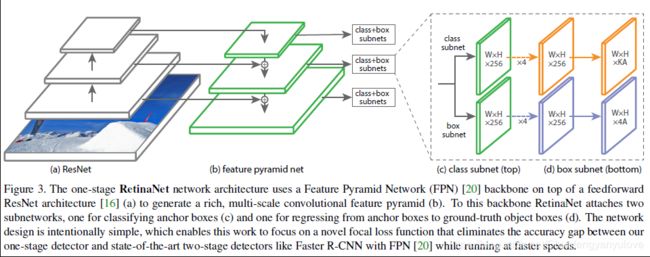
先来一张网络结构图:
相信对FPN比较熟悉的同学会发现,这跟FPN好像啊。
没错,作者的backbone采用的就是FPN,下面对这个网络逐一介绍一下:
-
backbone:FPN
RetinaNet的backbone采用Resnet-FPN结构,并在P3-P7上建立图像金子塔 P l P_l Pl代表其缩放比例是 2 l 2^l 2l倍。同时作者指出,FPN结构还是很有用的,最开始作者只使用Resnet最后一层的feature,结果AP(准确率)并不高。
-
anchors:
作者在原来的基础上,新增了3个size,{ 2 0 2^0 20, 2 1 / 3 2^{1/3} 21/3, 2 2 / 3 2^{2/3} 22/3}
-
正负样本的定义
IOU > 0.5 为正样本。
IOU [0, 0.4) 为负样本。
IOU [0.4, 0.5] 不要了。这里负样本的阈值被提到了0.4(大部分都是0.3),不知道是不是作者有意为之,来证明自己的网络可以容纳更多的正负样本不均衡。但是这样其实也带来了更多的hard examples.
检测部分,当然是正样本去检测就行了。
-
分类分支:
对于每一个FPN分支,都会有一个预测分支与之对应,了解SSD的小伙伴对这里应该不会陌生,分类分支包括4组3*3卷积+ReLU,最后接KA个3*3卷积。K代表类别,A代表anchor的数量。相比较于RPN网络,这里的网络更深了。
有一句话没有理解:parameters of this subnet are shared across all pyramid levels. -
box regression分支:
首先,box regression与分类分支并没有共享网络,结构与分类分支基本一致,只是在最后的卷积核的数量是4A个,因为要对每个anchor预测4个坐标。
在inference过程中,为了提高速度,RetinaNet只使用前1000的Prior去进行坐标回归,并且最后对所有的预测结果进行非极大值抑制,并设置阈值为0.5进行过滤,最终得到预测结果。
Focal Loss使用在分类分支中。
在训练的过程中,RetinaNet直接使用约100k左右的anchor进行训练,而不需要想SSD那样使用OHEM或者像RCNN系列那样提取候选区域,最终的loss是这100K的focal loss的和,并且作者表示,在 γ \gamma γ=2, α \alpha α=0.25的时候,网络效果最佳。
-
参数初始化
FPN部分参考FPN的初始化方法,其他的新添层,w采用高斯分布, σ \sigma σ=0.01, b=0, 最后一个卷积层 b = − l o g ( ( 1 − p i ) / p i ) -log((1-pi)/pi) −log((1−pi)/pi) pi = 0.1
实验部分
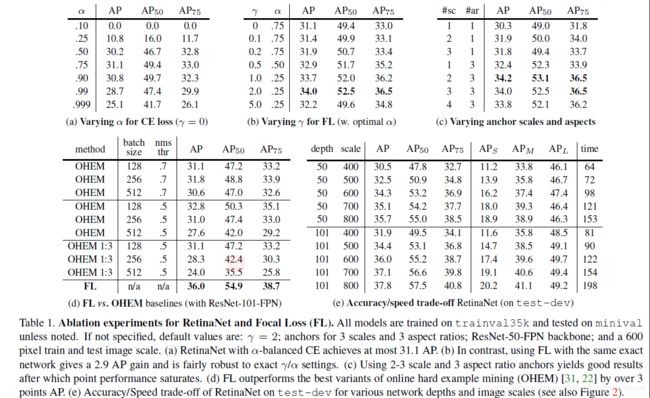
下表是一些对比实验
- ( a ) 是对crossentropy loss使用不同的系数的结果,可见当 α \alpha α=0.75的时候,表现最好。
- ( b ) 是使用focal loss的对比结果,其中加粗的为最好的效果。
- ( c ) 是使用不同比例、大小的anchor的结果对比。
- ( d ) 是对OHEM的对比结果,作者分别对OHEM设置不同的比例,以及使用focal loss的结果,结果显示使用OHEM并没有特别大的变化,但是使用focal loss精度提升明显,这也说明了focal loss的作用。
- ( e ) 是对不同尺度图像的精度以及速度的对比。
为了分析Focal Loss的效果,作者选取了大量的正负样本,然后分别计算Focal Loss,然后对其进行normalize操作,使其和是1,其累计分布如下图所示:
其横轴是样本的数量百分比,纵坐标是累计误差,可见, γ \gamma γ对于负样本的影响相对较大,特别是当 γ \gamma γ取2的时候,负样本的loss大部分的损失都是很小的,只有一小部分的loss比较大,这也说明了focal loss起到了对简单负样本的抑制作用,使得大部分负样本没有作用。
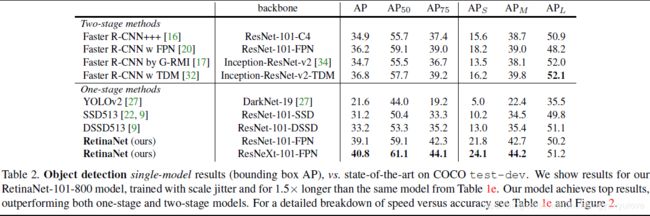
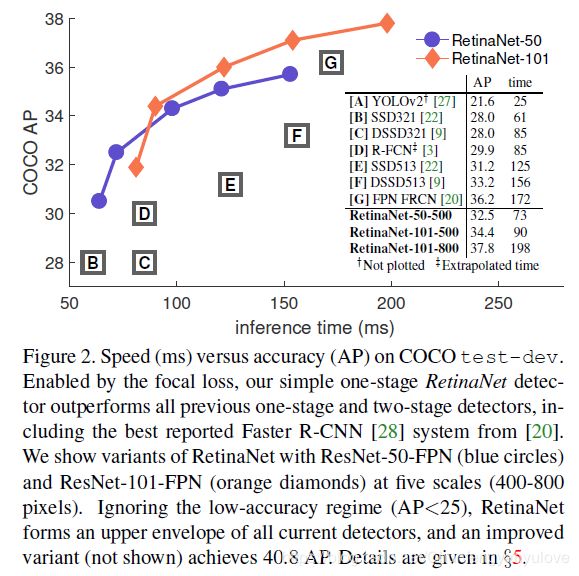
下面是网络的检测精度,以及速度,以及与state of the art网络的对比。
观察下面两张图,可以发现AP不太一样,主要原因是,其采用了一些策略,比如尺度变换等。
以上是对Focal Loss以及RetinaNet的一些理解,如果有不对的地方,欢迎指正