CenterNet: Keypoint Triplts for Object Detection 论文阅读笔记

论文名称:CenterNet: Keypoint Triplts for Object Detection

作者：Kaiwen Duan & Song Bai等

论文链接：https://arxiv.org/abs/1904.08189

代码链接：https://github.com/Duankaiwen/CenterNet

---

简要概述文章精华

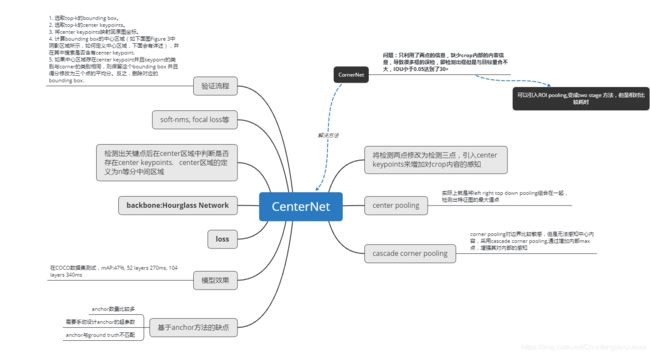
本篇文章是一篇anchor free的目标检测方法，主要是在CornerNet(该篇文章很经典，还没总结，后面补上)的基础上发展而来。文章的主要思想在于：CornerNet中只检测目标的左上角点和右下角点，bounding box错检率会比较高（即检测出目标框但是与目标重合比较少，这也是keypoint检测的常见问题），作者分析错检的主要原因在于-------在进行Corner检测的时候，没有关注bounding box内部的内容信息，所以作者提出了CenterNet，在利用CornerNet检测出bounding box，同时，在bounding box内部检测center keypoint来帮助过滤掉错检框，也就是文章标题所示的Keypoint Triplts，检测三个点，同时，作者提出了center pooling以及cascade corner pooling方法，center pooling用于检测center keypoint,cascade corner pooling用于加强原本corner point的检测，使得corner的检测的时候可以get更多的bounding box内部的内容信息。结果是该网络也取得了精度和召回的双重提升，在COCO上测试，mAP可以达到47%，52-layer hourglass 耗时大约在270ms.

下面详细介绍一下本文的重点

基于anchor的目标检测方法，利用anchor去拟合目标区域取得了很大的成绩，但其也存在一定的缺点：1.需要大量的anchor来保证跟ground truth的重合率，2.anchor一般都是手动设计的，3.手动设计的anchor往往与真实的物体框还是有一定的差距的，4.大量的anchor导致正负样本不均匀问题。

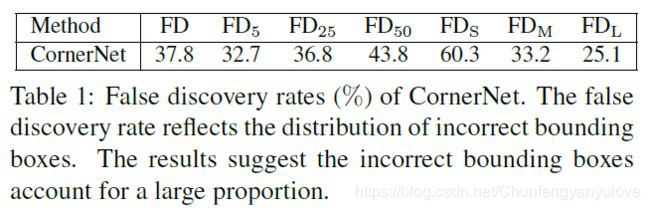
为了尽可能避免使用anchor这些问题，anchor free方法被提出，比较典型的代表就是CornerNet，该网络的灵感来源于关键点检测，通过直接检测目标的左上角点和右下角点的方法来检测目标区域，并且取得了不错的效果。但是其也存在一定的问题，那就是只检测两个点，缺少对中心内容的感知，这样就容易产生检测点的误匹配。如下图Figure 1第一行所示，红框便是错误的框。Table 1展示的是作者统计COCO数据集中CornerNet的错检率（false discovery rates）。可见整体还是比较高的，其中32.7%的检测框与groud truth的IOU重合率小于0.05%，43.8%的小于50%，在小样本中，占比更高，达到了60.3%.

为了解决这个问题，作者提出了centerNet，如下图第二行所示，通过中心keypoint对中心内容进行感知，正常情况，中心keypoint的类别应该跟坐标框的类别相同，利用这种方法来过滤掉错误的匹配框。

本文方法详解

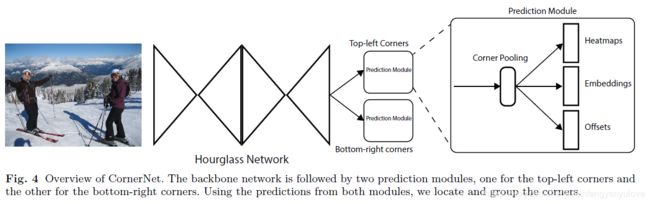
在介绍CenterNet之前，先简单介绍一下CornerNet是怎么做的，下图（Fig. 4）是CornerNet的结构图，backbone采用的是Hourglass结构(这是关键点检测常用的网络)，然后会接两个分支，分别用于检测左上角点以及右下角点，每个分支又会输出三个向量，分别对应Heatmaps，Embeddings，Offsets，heatmaps代表的是不同类别的keypoints的位置，以及对应的score，embeddings代表的是哪些keypoints是属于一个bounding box的，offsets是特征图到原图的映射，对keypoints进行微调的。

那既然，已经猜想出问题出在在进行关键点检测的时候，没有get到bounding box内部的信息，除了本文提出的，又有哪些方法可以解决呢？文章中也提到了，可以采用two-stage方法，后面再接一个ROI-pooling，去识别内部信息，但是耗时会增加比较多。

好了，下面进入正题，今天的主角CenterNet.

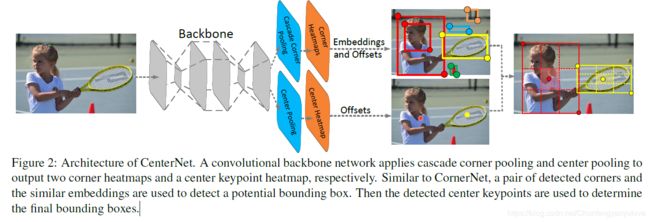
下图Figure 2 所示为CenterNet结构图，对比CornerNet，本文方法多增加了一个分支用于检测目标中心，同时，将目标中心的类别与Corner检测结果相合并。

具体是这么做的呢？
假设我们已经通过上面的网络得到了corners keypoints以及center keypoints的输出，那么后面的逻辑如何融合呢？具体的操作流程如下：

1. 选取top-k的bounding box。
2. 选取top-k的center keypoints。
3. 将center keypoints映射回原图坐标。
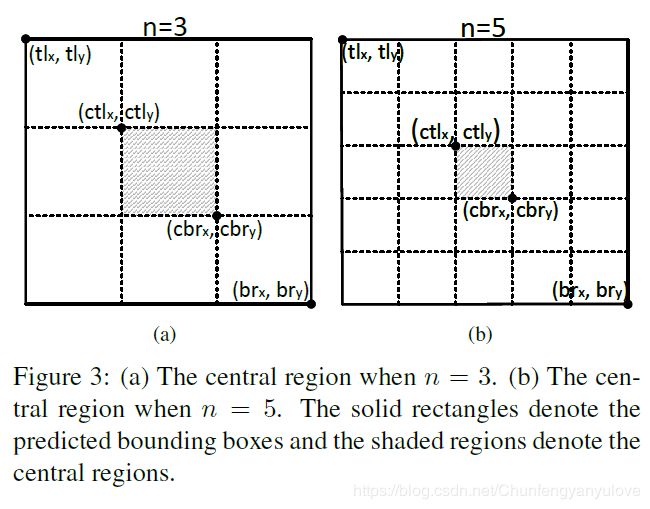
4. 计算bounding box的中心区域（如下面图Figure 3中阴影区域所示，如何定义中心区域，下面会有详述），并在其中搜索是否含有center keypoint.
5. 如果中心区域存在center keypoint并且keypoint的类别与corner的类别相同，则保留这个bounding box 并且得分修改为三个点的平均分。反之，删除对应的bounding box.

中心区域的定义

如果中心区域定义的太大，那么对大物体的精度会下降；如果定义的中心区域太小，那么对小物体的召回又会下降。所以本文有提出了一种动态的中心区域选取方法，公式如下，公式看起来挺复杂，但是结果很好理解，就是下图Figure 3，如果n=3，其实就是对bounding box进行三等分，然后去中间的区域，n=5就是对其进行5等分，然后取中间区域。

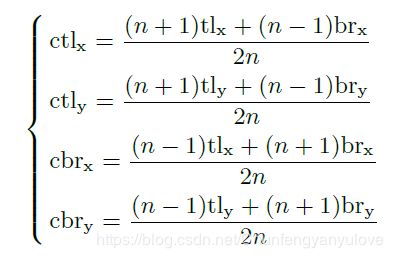
下面介绍一下本文另外两个创新点，center pooling 以及cascade corner pooling

在介绍center pooling以及cascade corner pooling之前，先来回忆一下CornerNet中提到的left pooling以及right pooling。，如下图所示，分别是left pooling以及top pooling，看图应该就一目了然了。

center pooling

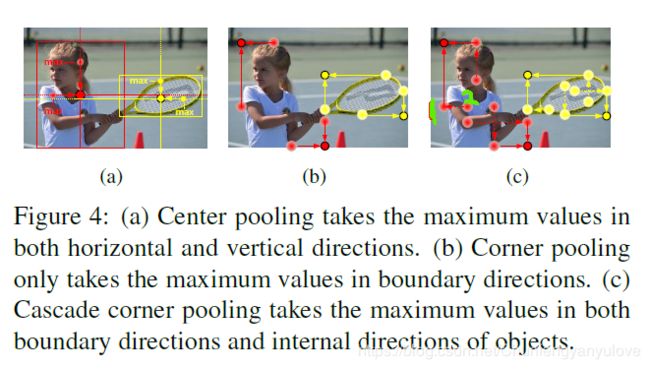
center pooling的目的是找到图像中的center keypoint（即行列都比较大的点）
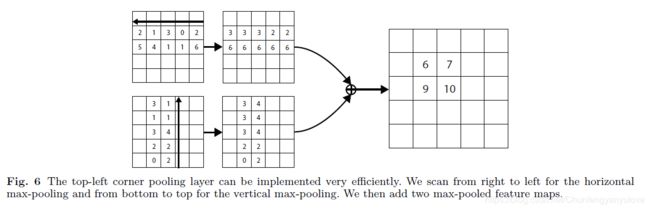
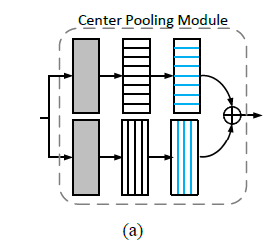
center pooling的做法也很简单，即通过在水平垂直的方向检测特征图的最大值，如图Figure 4a所示为Center pooling示意图。center pooling的具体做法就是如下图，上面代表：left pooling -> right pooling，下面代表 down pooling -> top pooling，然后将结果进行element-add操作。这就找到了中心最大点。

举个例子：
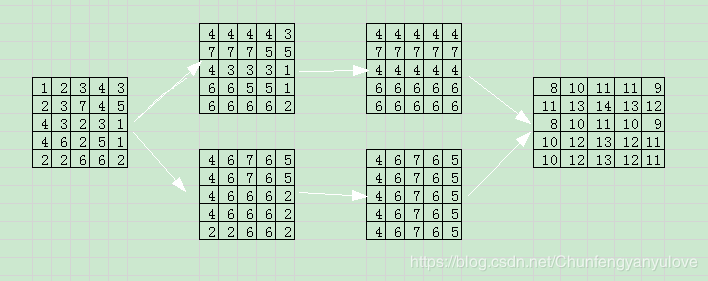
第一行依次是left pooling, right pooling，第二行依次是top pooling down pooling ,最终add到一起，根据值的大小就可以依次选出行和列的的极致情况，显然图中14是最大的，对应到原图7也是最大的。

cascade corner pooling
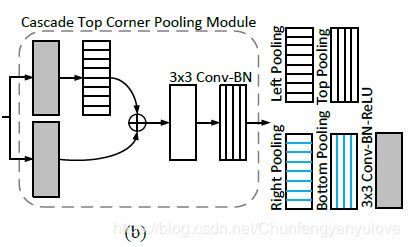
cascade corner pooling在corner pooling的基础上，增加了更多的内部的内容信息。Figure 4:©所示即为cascade corner pooling,主要思想就是不仅仅找到边缘的最大值，同时，将corner内部的内容也加到corner keypoints上面，提高corner keypoints对内容的感知能力，实际的做法就是如下图（b）所示为Top Corner Pooling，首先做一个left pooling，然后与原图求和，后面再过一个top pooling，这样就图中1和2都加到了left-topcorner上，同样的再做left corner pooling, down corner pooling right corner pooling就OK啦。

实验分析

不同网络的精度对比结果如下：

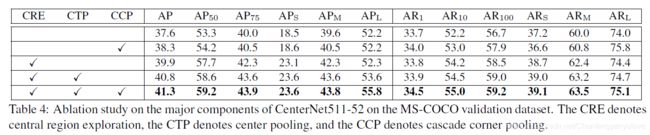
另外，作者做了溶解实验，来对比本文主要的三个关键点的效果提升，其中CRE代表central region exploration ,CTP代表center pooling, CCP代表cascade corner pooling，可见CRE效果提升是最明显的，也侧面说明了增加对中心内容的感知的重要性。

总结

本文是在CornerNet基础上发展来的，主要提到的就是3个重点，一个是中间区域信息的引入思想，另外两个分别是Center Pooling以及Cascade Corner Pooling，思想还是比较好的，值得学习。

最后附一张知识导图，帮助整理知识点

最后附上center pooling的代码，其他代码可以自行查看开头连接

class center_pool(pool_cross):
    def __init__(self, dim):
        super(center_pool, self).__init__(dim, TopPool, LeftPool, BottomPool, RightPool) ## 调用pool_cross

class pool_cross(nn.Module):
    def __init__(self, dim, pool1, pool2, pool3, pool4):
        super(pool_cross, self).__init__()
        self.p1_conv1 = convolution(3, dim, 128)
        self.p2_conv1 = convolution(3, dim, 128)

        self.p_conv1 = nn.Conv2d(128, dim, (3, 3), padding=(1, 1), bias=False)
        self.p_bn1   = nn.BatchNorm2d(dim)

        self.conv1 = nn.Conv2d(dim, dim, (1, 1), bias=False)
        self.bn1   = nn.BatchNorm2d(dim)
        self.relu1 = nn.ReLU(inplace=True)

        self.conv2 = convolution(3, dim, dim)

        self.pool1 = pool1()
        self.pool2 = pool2()
        self.pool3 = pool3()
        self.pool4 = pool4()

    def forward(self, x):
        # pool 1
        p1_conv1 = self.p1_conv1(x)
        pool1    = self.pool1(p1_conv1) ## 这里先来个top pooling
        pool1    = self.pool3(pool1)    ## 接着来个 down pooling

        # pool 2
        p2_conv1 = self.p2_conv1(x)
        pool2    = self.pool2(p2_conv1)   ## left pooling
        pool2    = self.pool4(pool2)      ## right pooling

        # pool 1 + pool 2
        p_conv1 = self.p_conv1(pool1 + pool2)  ## add 
        p_bn1   = self.p_bn1(p_conv1)

        conv1 = self.conv1(x)
        bn1   = self.bn1(conv1)
        relu1 = self.relu1(p_bn1 + bn1)

        conv2 = self.conv2(relu1)
        return conv2