利用keras破解captcha验证码
本文参考了知乎上的一篇文章,只做了少许改动,感觉挺好玩的,自己实现了一下,准确率比原作者的要高一些。如果想要了解原创文章的话,请移步知乎:使用深度学习来破解captcha验证码
本文通过keras深度学习框架来实现captcha验证码的识别,具体的环境配置如下:
Python:2.7.12
keras:1.2.2
theano:0.9.0rc2
captcha:0.2.4
numpy:1.12.0
matplotlib:1.5.3
所有的代码都已经开源在github上:https://github.com/chyang2015/keras_captcha
captcha是用Python写成的生成验证码的库,它支持图片验证码和语音验证码,本文使用的是图片验证码。与参考文章中的设置一样,我们的验证码的格式为数字加大写字母的组合。
先看一个利用captcha生成验证码的例子:
from captcha.image import ImageCaptcha
import matplotlib.pyplot as plt
import numpy as np
import pylab
import random
import string
characters = string.digits + string.ascii_uppercase
print(characters)
width, height, n_len, n_class = 170, 80, 4, len(characters)
generator = ImageCaptcha(width=width, height=height)
random_str = ''.join([random.choice(characters) for j in range(4)])
img = generator.generate_image(random_str)
plt.imshow(img)
plt.title(random_str)
pylab.show()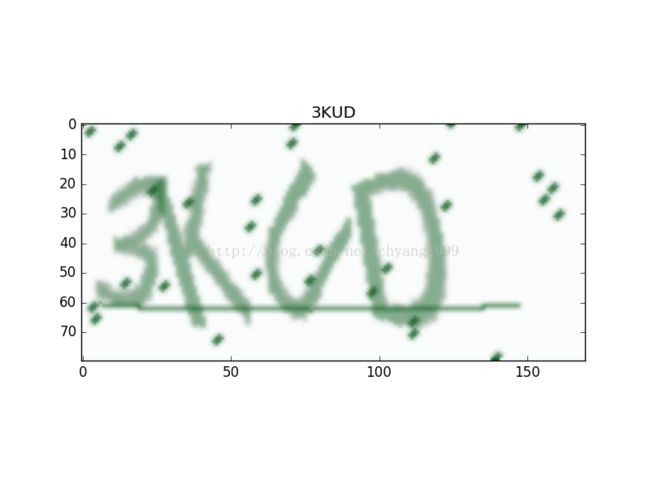
数据生成器
训练模型的时候,我们可以选择两种方式来生成我们的训练数据,一种是一次性生成几万张图,然后开始训练,一种是定义一个数据生成器,然后利用 fit_generator 函数来训练。
第一种方式的好处是训练的时候显卡利用率高,如果你需要经常调参,可以一次生成,多次使用;第二种方式的好处是你不需要生成大量数据,训练过程中可以利用 CPU 生成数据,而且还有一个好处是你可以无限生成数据。
X
X 的形状是 (batch_size, 3, height, width),比如一批生成32个样本,图片宽度为170,高度为80,那么形状就是 (32, 3, 80, 170),取第一张图就是 X[0]。
这里要注意的是keras后端在图像格式上的差异:tensorflow和theano的数据格式是不一样的:
tf(tensorflow)模式:(num, channel, height, weight)
th(theano)模式:(num, height, weight, channel)
要根据自己选择的后端的不同选择不同的数据格式,注意图像数据的转化。
y
y 的形状是四个 (batch_size, n_class),如果转换成 numpy 的格式,则是 (n_len, batch_size, n_class),比如一批生成32个样本,验证码的字符有36种,长度是4位,那么它的形状就是4个 (32, 36),也可以说是 (4, 32, 36),解码函数在下个代码块。
# 定义数据生成器,默认一批生成32张图片
def gen(batch_size = 32):
X = np.zeros((batch_size,3,height,width),dtype=np.uint8)
y = [np.zeros((batch_size,n_class),dtype=np.uint8) for i in range(n_len)]
generator = ImageCaptcha(height=height,width=width)
while True:
for i in range(batch_size):
random_str = ''.join([random.choice(characters) for j in range(4)])
X[i] = np.array(generator.generate_image(random_str)).transpose((2,0,1))
for j, ch in enumerate(random_str):
y[j][i,:] = 0
y[j][i,characters.find(ch)] = 1
yield X,y上面就是一个可以无限生成数据的例子,我们将使用这个生成器来训练我们的模型。
使用生成器
生成器的使用方法很简单,只需要用 next 函数即可。下面是一个例子,生成32个数据,然后显示第一个数据。当然,在这里我们还对生成的 One-Hot 编码后的数据进行了解码,首先将它转为 numpy 数组,然后取36个字符中最大的数字的位置,因为神经网络会输出36个字符的概率,然后将概率最大的四个字符的编号转换为字符串。
# 将概率最大的四个字符的编号转换为字符串
def decode(y):
y = np.argmax(np.array(y),axis=2)[:,0]
return ''.join([characters[x] for x in y])构建深度卷积神经网络
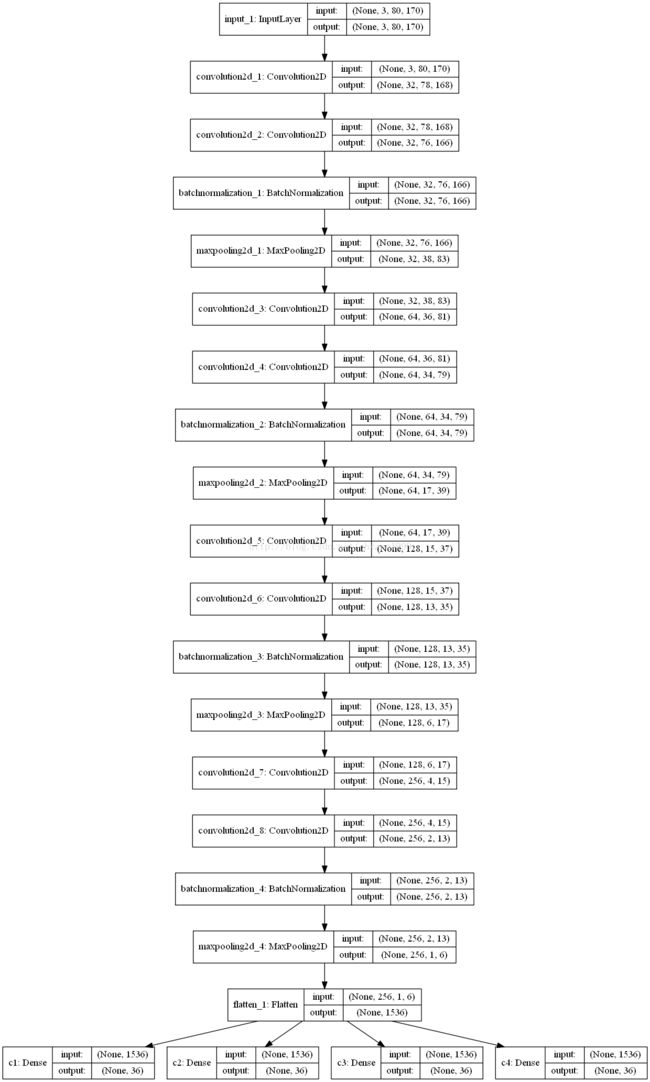
# 构建模型
def captcha_model():
width, height, n_len, n_class = 170,80,4,36
input_tensor = Input(shape=(3,height,width))
x = input_tensor
for i in range(4):
x = Convolution2D(32*2**i,3,3,activation='relu')(x)
x = Convolution2D(32*2**i,3,3,activation='relu')(x)
x = BatchNormalization(axis=1)(x)
x = MaxPooling2D((2,2))(x)
x = Flatten()(x)
x = [Dense(n_class,activation='softmax',name='c%d' % (i+1))(x) for i in range(4)]
model = Model(input=input_tensor,output=x)
return model 模型结构很简单,特征提取部分使用的是两个卷积,一个池化的结构,这个结构是学的 VGG16 的结构。之后我们将它 Flatten,然后添加 Dropout ,尽量避免过拟合问题,最后连接四个分类器,每个分类器是36个神经元,输出36个字符的概率。
模型可视化
训练模型
checkpointer =ModelCheckpoint(filepath="net-weight\\net-epoch.hdf5", verbose=1, save_best_only=True)
model.compile(loss='categorical_crossentropy',optimizer='adadelta',metrics=['accuracy'])
model.fit_generator(gen(),samples_per_epoch=51200,nb_epoch=5,validation_data=gen(),nb_val_samples=1280,callbacks=[checkpointer])
这里我设置了回调函数checkpointer,以保留训练过程中得到的最优模型的权重,预测的时候要加载权重。
测试模型
当我们训练完成以后,可以识别一个验证码试试看:from captcha_model import captcha_model
from captcha_generate_image import gen,decode
import matplotlib.pyplot as plt
import pylab
model = captcha_model()
model.load_weights("net-weight\\net-epoch.hdf5")
X,y = next(gen(1))
y_pred = model.predict(X)
plt.title('real:%s\npred:%s' % (decode(y),decode(y_pred)))
plt.imshow(X[0].transpose((1,2,0)),cmap='gray')
pylab.show()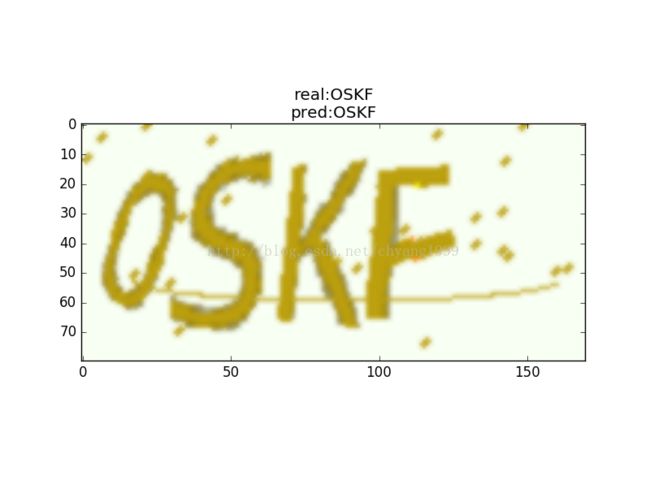
训练过程中的各种输出我也列在这里,可以看到,最终每个类别的准确率几乎都达到了98%,效果还是比参考文章中略高一些。
Epoch 1/5
51168/51200 [============================>.] - ETA: 0s - loss: 3.9187 - c1_loss: 1.1468 - c2_loss: 0.8826 - c3_loss: 1.0020 - c4_loss: 0.8873 - c1_acc: 0.6875 - c2_acc: 0.7496 - c3_acc: 0.7168 - c4_acc: 0.7520Epoch 00000: val_loss improved from inf to 0.82390, saving model to net-weight\net-epoch.hdf5
51200/51200 [==============================] - 648s - loss: 3.9164 - c1_loss: 1.1461 - c2_loss: 0.8821 - c3_loss: 1.0015 - c4_loss: 0.8868 - c1_acc: 0.6877 - c2_acc: 0.7497 - c3_acc: 0.7170 - c4_acc: 0.7522 - val_loss: 0.8239 - val_c1_loss: 0.1846 - val_c2_loss: 0.1971 - val_c3_loss: 0.2559 - val_c4_loss: 0.1863 - val_c1_acc: 0.9484 - val_c2_acc: 0.9477 - val_c3_acc: 0.9359 - val_c4_acc: 0.9453
Epoch 2/5
51168/51200 [============================>.] - ETA: 0s - loss: 0.3697 - c1_loss: 0.0706 - c2_loss: 0.0773 - c3_loss: 0.1280 - c4_loss: 0.0937 - c1_acc: 0.9780 - c2_acc: 0.9741 - c3_acc: 0.9583 - c4_acc: 0.9697Epoch 00001: val_loss improved from 0.82390 to 0.75851, saving model to net-weight\net-epoch.hdf5
51200/51200 [==============================] - 651s - loss: 0.3697 - c1_loss: 0.0706 - c2_loss: 0.0773 - c3_loss: 0.1280 - c4_loss: 0.0937 - c1_acc: 0.9779 - c2_acc: 0.9741 - c3_acc: 0.9583 - c4_acc: 0.9696 - val_loss: 0.7585 - val_c1_loss: 0.1449 - val_c2_loss: 0.1911 - val_c3_loss: 0.2266 - val_c4_loss: 0.1959 - val_c1_acc: 0.9703 - val_c2_acc: 0.9547 - val_c3_acc: 0.9523 - val_c4_acc: 0.9633
Epoch 3/5
51168/51200 [============================>.] - ETA: 0s - loss: 0.2306 - c1_loss: 0.0446 - c2_loss: 0.0498 - c3_loss: 0.0763 - c4_loss: 0.0600 - c1_acc: 0.9844 - c2_acc: 0.9820 - c3_acc: 0.9744 - c4_acc: 0.9797Epoch 00002: val_loss did not improve
51200/51200 [==============================] - 647s - loss: 0.2307 - c1_loss: 0.0445 - c2_loss: 0.0498 - c3_loss: 0.0764 - c4_loss: 0.0600 - c1_acc: 0.9844 - c2_acc: 0.9820 - c3_acc: 0.9743 - c4_acc: 0.9796 - val_loss: 1.4278 - val_c1_loss: 0.2712 - val_c2_loss: 0.3074 - val_c3_loss: 0.4099 - val_c4_loss: 0.4392 - val_c1_acc: 0.9305 - val_c2_acc: 0.9281 - val_c3_acc: 0.9016 - val_c4_acc: 0.8906
Epoch 4/5
51168/51200 [============================>.] - ETA: 0s - loss: 0.1713 - c1_loss: 0.0330 - c2_loss: 0.0399 - c3_loss: 0.0551 - c4_loss: 0.0433 - c1_acc: 0.9883 - c2_acc: 0.9856 - c3_acc: 0.9815 - c4_acc: 0.9854Epoch 00003: val_loss improved from 0.75851 to 0.58820, saving model to net-weight\net-epoch.hdf5
51200/51200 [==============================] - 647s - loss: 0.1712 - c1_loss: 0.0330 - c2_loss: 0.0400 - c3_loss: 0.0551 - c4_loss: 0.0432 - c1_acc: 0.9883 - c2_acc: 0.9856 - c3_acc: 0.9815 - c4_acc: 0.9854 - val_loss: 0.5882 - val_c1_loss: 0.1112 - val_c2_loss: 0.1240 - val_c3_loss: 0.1604 - val_c4_loss: 0.1925 - val_c1_acc: 0.9734 - val_c2_acc: 0.9719 - val_c3_acc: 0.9633 - val_c4_acc: 0.9570
Epoch 5/5
51168/51200 [============================>.] - ETA: 0s - loss: 0.1372 - c1_loss: 0.0271 - c2_loss: 0.0324 - c3_loss: 0.0411 - c4_loss: 0.0367 - c1_acc: 0.9904 - c2_acc: 0.9886 - c3_acc: 0.9859 - c4_acc: 0.9871Epoch 00004: val_loss improved from 0.58820 to 0.36915, saving model to net-weight\net-epoch.hdf5
51200/51200 [==============================] - 647s - loss: 0.1373 - c1_loss: 0.0271 - c2_loss: 0.0324 - c3_loss: 0.0410 - c4_loss: 0.0367 - c1_acc: 0.9904 - c2_acc: 0.9887 - c3_acc: 0.9859 - c4_acc: 0.9871 - val_loss: 0.3691 - val_c1_loss: 0.0730 - val_c2_loss: 0.0932 - val_c3_loss: 0.1108 - val_c4_loss: 0.0922 - val_c1_acc: 0.9852 - val_c2_acc: 0.9789 - val_c3_acc: 0.9742 - val_c4_acc: 0.9836总结
总的来说,今天一天就干了这么多事情,特别感谢原作者分享的文章,既让自己有个实战的参考,也能基于原作者进行一些网络上的改进。原作者后面提到的改进方法基于一类特殊的循环神经网络GRU,由于自己在这方面没有什么研究,就不献丑了。
参考文章:使用深度学习来破解captcha验证码