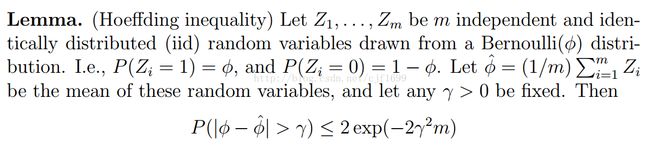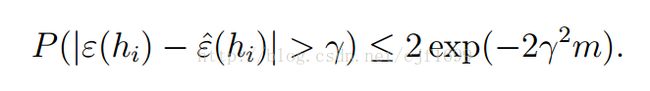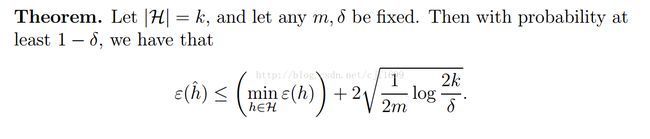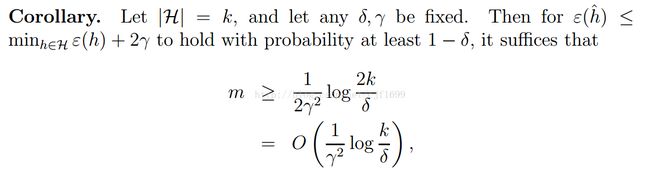【学习笔记】斯坦福大学公开课：cs229 Part 6 Learning Theory【上】

今天进入到cs229的学习理论部分，这一部分说简单也简单，毕竟在Coursera上学过一遍Ng的课，关于bias/variance tradeoff的相关内容有了一些了解，可是cs229里一上来证明，还是值得好好琢磨琢磨的。那么这节课讲了什么呢？

前面学的是算法，无论是线性回归、逻辑回归、广义线性模型、指数分布族，还是朴素贝叶斯、SVM，以及涉及到的梯度下降法、牛顿法、最大似然估计、拉普拉斯平滑等等，都是一些具体的方法，在战场上叫做“战术”，相当于我们的武器。不过打仗不能凭借一腔奋勇之情，还得讲究方法和谋略。那么学习理论就是告诉我们如何战略布局，从根本上如何决策，以及为什么要这样决策的。

1 Bias/variance tradeoff偏差/方差权衡

简而言之，模型的参数过少时，根本无法根据输入准确地预测输出，比方说我的数据本来是二次分布，你拿一个线性函数来糊弄我，那肯定不行，这时无论是训练误差还是泛化误差（就是测试集上的误差）都比较大，术语叫“high bias”；

模型的参数过多时，就会“过犹不及”，在已知的训练集上，模型表现的很好，百发百中，没有一个预测错误的；但是一到测试集上就露出马脚了。就仿佛你把书上的题目都背会了，考试时来个没见过的题目，就懵圈了。本来我就是一个二次函数分布，抛物线的形状简洁得很，你来了个五次函数的曲线，几里拐弯的，怎么可能预测的准。这时，训练误差很小，泛化误差很大，术语叫“high variance”。

那么，我们追求的，就是二者之间的平衡。

2 预热——两条引理

上面说到训练误差和泛化误差，而训练一个机器学习模型时我们只能知道前者，而看不到后者，所以这两种误差之间有什么联系呢？能否根据训练误差很小就判断出泛化误差也很小呢?

首先安德鲁老师抛出了两条引理。一个是概率论中的公理：一堆事件中至少有一件事发生的概率一定不会超过这堆事件的发生概率总和。

另外一个是霍弗丁不等式：

什么意思？说的是z1到zm是m个独立同伯努利分布的随机变量，即要么是0，要么是1，每个随机变量的数学期望都是ϕ，那么，这m个变量一经生成（比如做了m次独立重复试验），我就可以用他们的平均数来估计他们每一个的期望，也就是ϕ，并且对于任意小的整数γ，估计误差超过γ的概率都不超过不等式右面的式子。

这俩引理对于接下来的论证很有帮助。为了简便，安德鲁老师使用二元分类问题举例说明，可以推广到回归问题以及多分类问题。假设每组训练数据（xi,yi）都是独立同分布的，服从某种概率分布D。好的，表演开始。

这节课的符号很多，我偷个懒，就不详细写了。首先定义我们的经验风险，也叫经验误差：empirical risk（empirical error），他其实说的就是m组训练数据中，误分类所占比例，也就是用我们学习到的模型（假设）去预测输出，和实际输出不相符的数据所占整体的比例。那么泛化误差（generalization error）的定义就是我们依据概率分布D抽取一组新数据（x,y），我们的模型会误分类的概率P。

ERM（empirical risk minimize）经验风险最小化其实我们已经接触过了，在线性分类中，我们就曾经试图找到一组参数θ，根据θ transpose x的正负来划分h(x)是0还是1，做法就是用最大似然（梯度下降）等方法，找到使cost function最小的θ，这其实就是ERM。为了更具普适意义，现在我们说，我们是要在整个假设空间中找到某种假设（不一定是线性的了，有可能是神经网络那样的），使得在这种假设下，经验误差最小。

3 假设空间有限

先来考虑假设空间中只有有限个（k个）假设的情况。

我们要套用之前的理论去做一些事情。从假设空间中随意选取一个h，我们让一个伯努利变量Z来指示h表现的怎么样，要是分类错误，Z=1，分类正确，Z=0. 注意，这里有两套符号，Z对应h在测试集上的表现（即新的example），Zj(1≤j≤m)对应h在训练集上的表现。

注意到，由于bernoulli分布的特点，Z的数学期望，就等于Z=1的概率ϕ，就等于我们的泛化误差（上文提到，泛化误差就是模型在new example上误分类的概率），而经验误差，则可表示为Zj们的平均值，因此，根据引理2，我们就做出以下估计：

带帽的是经验误差，不带帽的是泛化误差，也即bernoulli分布的数学期望。我们看到，前者对后者做了一个漂亮的估计。

但是注意，这里只是针对假设空间H中的其中一个假设我们做出了这样的保证，而我们要的是对H中所有假设，都满足这一点，那么引理1就要出场了。

事件 Ai表示的就是对于假设空间中第i个假设，它对应的经验误差和泛化误差相差超过了γ的概率（我们姑且叫做演砸了），正因如此，使用引理1就是在算至少有一个假设演砸了的概率，因此，取个非，就是所有假设都演得很棒的概率了~并且，这个概率相当的高，注意到，对于任意γ>0成立，又是指数衰减，因此这个概率非常接近1了。这个结果叫做uniform convergence。

我想，这大概已经可以说明用ERM训练模型在理论上的可行性了，然而我们还是要深究一下。

注意到，有三个变量，m,γ,还有概率误差，即那个绝对值项，我们可以根据任意两项确定第三项。比如，我们希望所有假设演技都棒的概率越大越好，如果令δ=2kexp(-2γ2m)，那么当

 

时，就会达到我们的期望效果。上式表明，如果要使用ERM，我们至少需要多少训练数据。能够do a good performance的m，我们叫它sample complexity。注意到,m是k的对数函数，这很漂亮。

现在我们已经说明了，对于假设空间H中每一个假设，都可以用经验误差近似的代表它的泛化误差，让其经验误差最小，基本上也就做到了泛化误差最小，即达到准确预测的目的。不过，这里用了“基本上”，即还是会存在一些偏差的。也就是说，我们使用经验误差最小化，在H中挑了一个最好的假设h^，这个h^和真正能使得泛化误差最小的某个同样在H中的h*可能并不是同一个假设。那么，h^和h*在泛化误差方面，表现得究竟差了多少呢？两次利用绝对值项，并注意到“带帽”和“不带帽”分别代表的是经验误差和泛化误差，对h^和h*便有：

于是看到了，我们根据ERM选出来的h^比理想情况下的h*坏不到哪里去，最多不超过2γ！好了，现在我们可以把上述归纳成一个定理了：

以及一个推论：

再说最后一个问题！

根据我们的定理，其实可以看出一些关于bias/variance tradeoff的端倪。如果我们扩大假设空间H变成H‘，在H’中选择模型，那么定理中第一项只会变小（因为H是H‘的子集），而到了H’之后，由于k变大了，第二项就会变大。这就说明，如果我们在更大的假设空间中选择模型（简单理解为，线性模型中，我们考虑更高次的多项式函数），偏差只可能变小，而方差则可能会变大，这和我们最开始的论述是一致的。

好了，下一篇笔记中，我再接着记录H中假设数目无限的情况下的学习情况~

（图片来源：Andrew Ng ，Stanford University cs229讲义）

********分割线************

PS：经历了各种偷懒，拖了不知道几天之后，终于，，，把这篇写完了[捂脸]