LeetCode 514: Freedom Trail 解题与思考

LeetCode 514: Freedom Trail 解题与思考

[原题链接]

题目描述

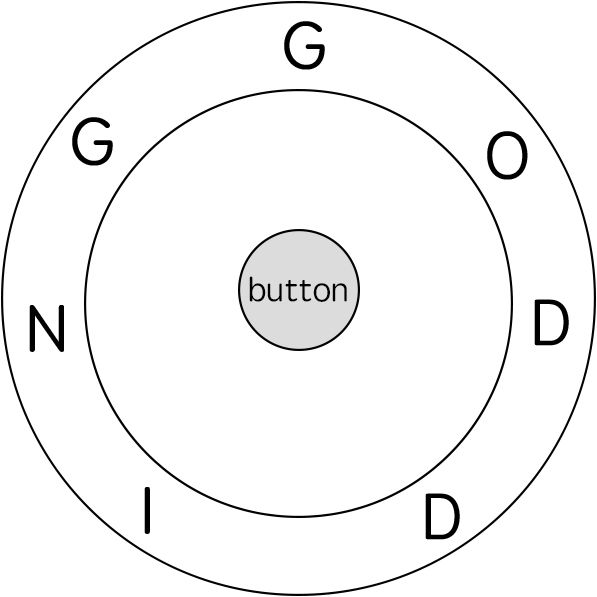
我们有一个轮盘，轮盘上有一个首尾相接的字符串S，我们有如下操作
1、转轮盘到下一个或者上一个字符，需要一步操作
2、输出当前字符，需要一步操作
假如我们有目标字符串K，求取出K的最小操作步数

思路

第一感觉就是用DP，因为看上去除去末尾的“上一个字符串”所需要的距离，加上从上一个最小距离，然后求极小值，就是所需答案。
但是遇到了几个问题：

• 假设结束的字符为E，在轮盘中有若干个相同的E，你不知道以哪个结尾是最优解
• 你也不知道上一个字符串的末尾停留在哪个位置时能取到最优解

所以我们至少要把问题稍微做一下转换：

Step1
假设字符串 Kn 长度为n，以 En 结尾，有p个E( En,1,En,2,....,En,p )(此处每个变量分别记录其所在位置)，那么，我们就是在寻找以某个位于 En,i 结尾所得到的字符串K所用步数最少。
记字符串 Ei 结尾所需要的步数为 Sn(En,i) ，记得到长度为n的字符串K的最小步数为 Kn 即

得到K的最少步数=min(Sn(En,i))−−①

Step2
然后这个时候我们需要求解 Sn(En,i) ，问题就变成：求解以某个特定位置 En,i 结尾的得到K的最小步数。这个问题就是很明显的DP了。
不妨设上一个字符串为 Kn−1 ，结尾字符为 En−1 ， 假设我们已经求得 Sn−1(En−1,j) ，也即以位置 En−1,j 结尾的时候所需的最小步数，那么我们只要找出从所有 En−1 中出发到达 En,i 中所用步数最少的，就是以特定位置 En,i 结尾的最小步数，即

Sn(En,i)=min(Sn−1(En−1,j)+En−1,j到En,i的最小步数)−−②

于是递推式就出来了。其中 Sk 则为最优子问题。

算法

设计一个栈，栈内元素为二元对，记录了某个字符c的位置以及到达c耗费的最小步数

假设有两个这样的栈，一个为now，一个为last，分别记录当前结尾字符所在位置以及最小步数，和上一个结尾字符所在位置以及最小步数

初始化：我们将轮盘开始字符压now栈，最小步数为0；
以n记录取到字符串的第几个

循环做以下步骤：
1、将now的元素移动到last
2、对于字符串 Kn ，假设结尾字符为 En ，对每个 En,i ，从last栈中取出所有的元素，按照②式与之计算最短路径，求最小值，然后压入now
3、n自加1

最后的解为now栈中所有最小路径中的最小值

代码

#include 
#include 
#include 
using namespace std;

class Solution {
    int distance(int a, int b, int size) {
        return (a < b) ? ((b - a > size / 2) ? (size + a - b) : (b - a)) : ((a - b > size / 2) ? (size + b - a) : (a - b));
    }
public:
    int findRotateSteps(string ring, string key) {
        vector<vector<int>> charArr;
        vectorint, int>> sol, solNext;
        sol.push_back(pair<int, int>(0, 0));
        int nowChar = 0;
        charArr.resize(26);
        int i = 0;
        for ( auto c : ring ) {
            charArr.at(c - 'a').push_back(i++);
        }
        while ( nowChar != key.size() ) {
            for ( auto pos : charArr.at(key.at(nowChar) - 'a') ) {
                pair<int, int> best(pos, 100000);
                for ( auto nowpos : sol ) {
                    int dis = distance(nowpos.first, pos, ring.size());
                    if ( nowpos.second + dis + 1 < best.second ) {
                        best.second = nowpos.second + dis + 1;
                    }
                }
                solNext.push_back(best);
            }
            sol = solNext;
            solNext.resize(0);
            nowChar++;
        }
        int answer = 100000;
        for ( auto ans : sol ) {
            answer = (ans.second < answer) ? ans.second : answer;
        }
        return answer;
    }
};

思考

原题目是不怎么好DP的，需要绕个弯子，总的来说不难