数字滤波器的设计

数字滤波一般分为时域滤波和频域滤波。频域滤波是将时域变换到频域，对相应频率做调整，然后反变换到时域，抛开FFT的话过程相对简单。在这里我们主要说时域滤波。

时域滤波器分为无限脉冲响应IIR和有限脉冲响应FIR两种。IIR滤波器的优点是可以用较低的阶数（相比同样指标的FIR滤波器）实现滤波器。缺点一：不是线性相位，只能用于对相位信息不敏感的信号(如音频信号）。缺点二：有可能是不稳定的。在设计的过程中为了保持稳定性和因果性，要求z变换所有的极点都必须位于单位圆内。但即使是这样，也可能由于量化舍入等因素引起的误差最终导致IIR滤波器不稳定。FIR滤波器的优点是可以设计成具有线性相位的，并且是稳定的(FIR滤波器除原点处外没有极点)，缺点是阶数高，也就是说计算量大。

IIR滤波器设计：

IIR滤波器最终具有如下形式:

FIR滤波器最终为:

IIR滤波器的设计主要是将已经比较成熟的连续时间滤波器(如巴特沃兹滤波器，切比雪夫滤波器，椭圆滤波器)变换成满足指标的离散时间滤波器。主要方法使脉冲响应不变法和双线性变换法。

脉冲响应不变法：

脉冲响应不变法的核心思想是：让离散时间滤波器的脉冲响应和已有的连续时间滤波器的脉冲响应保持“相等”。这里当然不可能相等，可以理解为，离散时间滤波器的脉冲响应是对连续时间滤波器脉冲响应的“采样”。

设计过程如下：

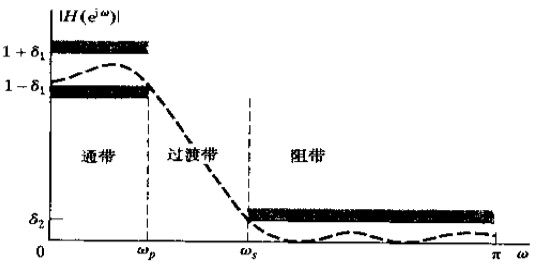
1，确定离散时间滤波器的技术指标。主要是通带截止频率，阻带截止频率，通带增益范围，阻带增益范围。下图摘自奥本海姆的《离散时间信号处理》。

  所以离散时间滤波器的技术的要求为:

  

  

2，将离散时间滤波器所要求的技术指标转换成连续时间滤波器对应的指标。

因为离散时间脉冲响应是连续时间脉冲响应的等间隔采样，所以离散时间滤波器与连续时间滤波器的脉冲响应有如下关系：

                     

Td是离散时间脉冲响应对连续时间脉冲响应的采样间隔，在实际中会被消掉，计算的时候可以取便于计算的值，比如1。注意到等式右边乘了Td，是为了保持两者在频域的幅度一致。

于是，两者的频率响应关系如下：

                

如果连续时间滤波器是带限的，并且满足:  对于，

 那么就有：

                   

比较和可以看出。 如果领Td=1，则。

于是根据这个对应关系以及离散时间技术指标的两个不等式可以计算出连续时间的技术指标:

3，选择连续时间滤波器，并按照2中的指标计算出连续时间滤波器的参数。

   以巴特沃兹滤波器为例：

   

这里需要确定两个参数，一个是N, 一个是。这两个参数可以由2中的不等式取边际值变成等式方程组求出。

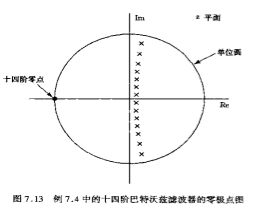
4, 得到了N和， 连续时间滤波器就确定了，可以在S平面确定出极点的位置。为了保证稳定性，需要取S平面虚轴左面的N个极点。由这些极点，可以得到Hc(s)的表达式（拉普拉斯变换)。

对于连续时间滤波器的系统函数，其对应的脉冲响应不变式的离散时间系统函数为: 

于是，既然我们已经得到了H(s)，就可以得到相应的离散时间滤波器的系统函数H(z)，进而得到时域的表达式。

至此，IIR滤波器通过脉冲响应不变法设计完毕！

在设计过程中发现有一点是要求连续时间滤波器是带限的，这就是说，连续时间滤波器只能是低通或带通，那么脉冲响应不变法就不适用于设计高通或带阻的滤波器！而且，实际中连续时间低通滤波器也不是完全带限的，不过如果在高频部分趋于0，那么混叠就很小，在设计滤波器时，可以在满足通带指标的同时，适当超过阻带指标来做一些补偿。

双线性变换法：

双线性变换的核心思想是：确定一种s和z的代数变换，用这种变换将s平面映射到z平面。设计过程如下：

1， 确定离散时间滤波器的技术指标。这一步和脉冲响应不变法相同。

2，将离散时间滤波器所要求的技术指标转换成连续时间滤波器对应的指标。

     这一步和脉冲响应不变法不同的是，在脉冲响应不变法中，有。而对于双线性变换法，映射关系是：

      , 也即 

     上面的公式来源于

                  ,       

     具体的公式推导这里就不详细写了，重点就是 Ω和ω的对应关系和脉冲响应不变法时不同了。

     接下来就可以按照这一对应关系，由1中 ω的截止频率和频率响应的幅度的不等式，得到 Ω对应的截止频率和不同频率响应的幅度的不等式，从而确定了连续时间滤波器的技术指标。

3， 选择连续时间滤波器，并按照2中的指标计算出连续时间滤波器的参数。这一步和脉冲响应不变式相同。

4， 根据N和 ，确定连续时间滤波器，得到H(s)，这一步也和脉冲响应不变式相同。

5， 根据H(s)，得到H(z)。

     这一步需要将带入H(s)，从而得到H(z)。这一步完成了双线性变换法从S平面到Z平面的映射。

6， 根据H(z)得到形如 的时域表达式。

以下是三种用双线性变换法得到低通滤波器H(z)的零极点图，摘自奥本海姆的《离散时间信号处理》

    

脉冲响应不变法的要求对应的连续时间滤波器必须是带限的。（否则会出现混叠)

双线性变换法的要求对应的连续时间滤波器必须具有分段恒定的幅度响应。因为其频率映射(连续时间频率到离散时间频率)是非线性的，引入了频率轴的非线性畸变。

FIR滤波器设计

FIR滤波器的设计方法主要是窗函数法。

所谓窗函数法，是说，假定有一个理想滤波器，那么它在时域具有非因果并且无限长的脉冲响应，为了在实际中应用，需要对该理想滤波器的脉冲响应h[n]加窗截断，来得到因果的并且有限长的脉冲响应。

因为时域加窗后频域也会相应改变，理想滤波器就变成了“非理想”滤波器。于是问题就变成了寻找一个合适的窗，使这个加窗截断后的“非理想”滤波器满足技术指标。

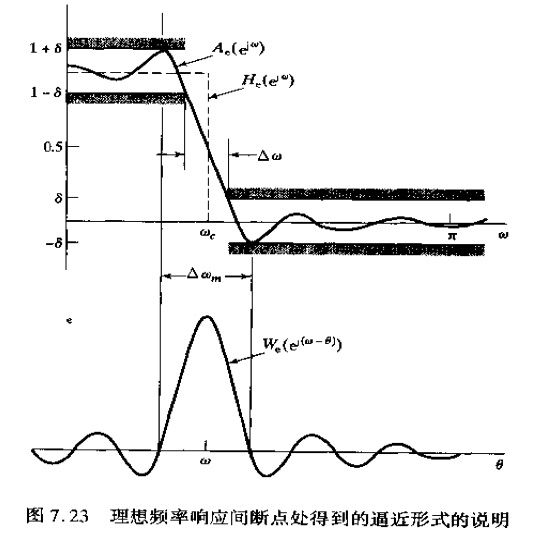
下图摘自奥本海姆的《离散时间信号处理》

为了满足FIR滤波器的因果性和线性相位，窗函数应该满足：

              

也就是w[n]是对于点M/2对称的。

通常所用的窗函数有：矩形窗，汉宁窗，海明窗，布莱克曼窗，凯撒窗等。

因为凯撒窗的形状可以根据参数调节，所以对于频域指标有明确限制时会选择凯撒窗，通过频域指标来确定凯撒窗的参数。

凯撒窗定义为：

式中α=M/2, 为第一类零阶修正贝塞尔函数。

所以凯撒窗也有两个参数：M和β。

设计过程：

1， 确定离散时间滤波器的技术指标。上图中的δ和通带截止频率，以及阻带截止频率。

2，定义为过渡区的宽度。并定义 用来计算β

    

    于是对于给定的δ就可计算出参数β。

3，参数M可以通过以下公式计算出：

    

     至此，凯撒窗的参数就完全确定了。

4，窗函数w[n]已经确定。如果理想滤波器的脉冲响应是h[n]，那么对应的FIR滤波器就是h[n]w[n]。

设计FIR高通滤波器:

如果已有了FIR低通滤波器，很容易就可以设计出相反的高通滤波器。

理想高通滤波器（广义线性相位）频响为：

可以看出， ，于是高通滤波器的时域表示为：

而且可以通过这种方式得到多通带多阻带的滤波器。