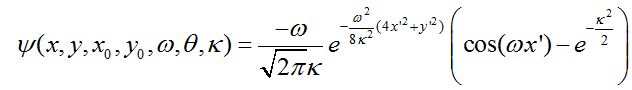竞争编码
竞争编码
摘要
竞争编码(competitive coding scheme[1])是目前掌纹识别方法中效果非常好的一种,具有特征占用空间小,匹配速度快,识别精度高等优势[2]。本文首先简要介绍该方法,随后给出其核心部分之一——构建Gabor滤波器的C++语言实现代码,最后给出该方法在香港理工大学公开库(v2)上身份验证(verification)实验的结果。
1 引言
2004年,AdamsWai-Kin Kong等[1]提出了用于低分辨率掌纹识别的竞争编码方法。该方法具有特征占用空间小,匹配速度快,识别精度高等优势,成为低分辨率掌纹识别方法的state-of-the-art。根据文献[3]的分类方法,竞争编码属于掌纹识别中基于编码的方法这一类别。该类方法包括三个核心部分:滤波器,编码规则,以及匹配方式。对于滤波器,竞争编码选择了六个不同方向的Gabor滤波器的实部;对于编码规则,竞争编码采用“winner-take-all”规则,即只关心滤波结果中极值对应的方向,随后将其编码为3个比特;而对于匹配方式,竞争编码利用二进制的异或操作实现高效的匹配。
由于竞争编码中滤波器的参数选择对于最终的识别结果会产生重要影响,而目前公开的资料中却没有详细的参数信息。这就会导致该方法的可重复性较差,也就是说,后续研究人员按照文献[1]实现了竞争编码方法,其精度却远低于已有文献中给出的识别精度。因此,为了便利后续的掌纹识别方法研究,我们给出构建滤波器的C++语言代码,并以香港理工大学的掌纹公开库(v2)[4]为基准数据库,测试了选择不同的参数时该方法的身份验证(verification)实验的EER。这里给出的实验结果可以作为竞争编码在该库上训练参数的依据,也可以作为竞争编码在该库上识别精度的上限。
2 构建滤波器
构建滤波器时需要考虑的几点主要包括滤波器的大小,滤波器的实现公式,以及公式中的参数取值。这里我们选择35×35的滤波器大小[5, 6],Gabor滤波器的公式[7]
| (1) |
其中![]() ,
,![]() ,
,![]() 是该滤波器的中心,
是该滤波器的中心,![]() 和
和![]() 分别表示滤波器的频率和方向。
分别表示滤波器的频率和方向。![]() 定义为
定义为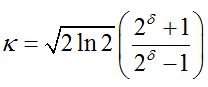 ,其中
,其中![]() 是频率响应。当
是频率响应。当![]() 和
和![]() 固定下来之后,
固定下来之后,![]() 可以通过
可以通过![]() 确定。构建滤波器的C++语言实现代码如下:
确定。构建滤波器的C++语言实现代码如下:
#include
// 滤波器大小
const int g_iFilterSize = 35;
const int g_iHalfFilterSize =g_iFilterSize/2;
// 滤波方向
const int g_iOrientation = 6;
// 滤波器的具体数值
double g_pfFilter[g_iOrientation][g_iFilterSize*g_iFilterSize]= {0};
// 构建某个方向的滤波器,前三个参数分别对应于公式1中的![]() ,
,![]() 和
和![]() 。
。
void BuildGaborFilterAngle(double fOmega,double fKappa, double fTheta, double* pFilter)
{
constdouble _2ln2 = sqrt(2*log(2));
doublefSigma = fKappa / fOmega;
doublefFactor1 = -fOmega / (sqrt(2*PI) * fKappa);
doublefFactor2 = -(fOmega*fOmega)/(8*fKappa*fKappa);
doublefSin = sin(fTheta);
doublefCos = cos(fTheta);
doublefFactor;
doublex, y, x1, y1;
doublefSum = 0;
inti, j;
for(i=0; i
{
x= i-g_iHalfFilterSize;
for(j=0; j
{
y= j-g_iHalfFilterSize;
x1= x*fCos + y*fSin;
y1= y*fCos - x*fSin;
fFactor= fFactor1 * exp(fFactor2*(4*x1*x1+y1*y1));
pFilter[i*g_iFilterSize+j]= fFactor * ( cos(fOmega*x1) - exp(-fKappa*fKappa/2) );
fSum+= pFilter[i*g_iFilterSize+j];
}
}
doublefMean = fSum / (g_iFilterSize * g_iFilterSize);
for(i=0;i
for(j=0; j
pFilter[i*g_iFilterSize+j]-= fMean;
}
// 构建全部六个方向的滤波器,参数分别对应于公式1中的![]() 和
和![]()
void BuildGaborFilter(double fOmega, doublefKappa)
{
doublefTheta;
inti;
for(i=0;i
{
fTheta= PI*i/g_iOrientation;
BuildGaborFilterAngle(fOmega,fKappa, fTheta, g_pfFilter[i]);
}
}
图1.滤波器的形貌
3 实验结果
我们首先利用上一篇文章提到的预处理方法获取香港理工大学掌纹公开库的ROI图像,随后以不同的参数构建滤波器,并根据身份验证实验测试竞争编码方法的精度,结果如表1所示。
表1.竞争编码中Gabor滤波器不同的参数取值对应的EER(%)
|
|
0.1 |
0.2 |
0.3 |
0.4 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
1 |
| 0.1 |
4.5162 |
31.8045 |
34.6238 |
32.0035 |
32.5016 |
32.0753 |
32.1757 |
32.9526 |
33.0047 |
33.1685 |
| 0.2 |
0.0629 |
4.6147 |
25.5948 |
31.8098 |
31.3643 |
34.5768 |
32.6908 |
31.9973 |
32.0482 |
32.5224 |
| 0.3 |
0.0424 |
0.1831 |
4.7377 |
20.3330 |
29.6424 |
31.8269 |
31.3708 |
31.0372 |
34.4988 |
31.7868 |
| 0.4 |
0.1437 |
0.0658 |
0.3796 |
4.9009 |
16.5864 |
26.4293 |
30.7706 |
31.8337 |
31.7740 |
31.3116 |
| 0.5 |
0.4173 |
0.0515 |
0.1270 |
0.6549 |
5.2761 |
14.8493 |
23.4143 |
28.4554 |
31.5613 |
31.8353 |
| 0.6 |
0.7957 |
0.0435 |
0.0697 |
0.2081 |
1.0394 |
5.4991 |
13.7736 |
21.3956 |
26.6101 |
30.1823 |
| 0.7 |
1.0810 |
0.0553 |
0.0531 |
0.1183 |
0.3178 |
1.5012 |
5.8644 |
12.8980 |
19.7228 |
24.9977 |
| 0.8 |
1.3093 |
0.1066 |
0.0485 |
0.0752 |
0.1570 |
0.4875 |
2.0073 |
6.2558 |
12.6445 |
18.6218 |
| 0.9 |
1.4708 |
0.1970 |
0.0405 |
0.0611 |
0.1080 |
0.2441 |
0.7357 |
2.5919 |
6.9901 |
12.6715 |
| 1 |
1.5979 |
0.3240 |
0.0451 |
0.0495 |
0.0764 |
0.1428 |
0.3550 |
1.0937 |
3.3406 |
7.3262 |
| 1.1 |
1.6759 |
0.4509 |
0.0497 |
0.0473 |
0.0670 |
0.1139 |
0.2224 |
0.5151 |
1.6079 |
4.1354 |
| 1.2 |
1.7264 |
0.6113 |
0.0747 |
0.0402 |
0.0579 |
0.0822 |
0.1565 |
0.3257 |
0.8316 |
2.2293 |
| 1.3 |
1.7605 |
0.7316 |
0.1042 |
0.0429 |
0.0499 |
0.0730 |
0.1227 |
0.2265 |
0.4818 |
1.2441 |
| 1.4 |
1.8166 |
0.8472 |
0.1441 |
0.0397 |
0.0458 |
0.0694 |
0.0992 |
0.1652 |
0.3344 |
0.7453 |
| 1.5 |
1.8474 |
0.9405 |
0.1841 |
0.0438 |
0.0440 |
0.0606 |
0.0843 |
0.1432 |
0.2511 |
0.5275 |
| 1.6 |
1.8901 |
1.0254 |
0.2341 |
0.0464 |
0.0406 |
0.0568 |
0.0735 |
0.1252 |
0.2073 |
0.3721 |
| 1.7 |
1.8915 |
1.1068 |
0.2784 |
0.0505 |
0.0403 |
0.0515 |
0.0721 |
0.1155 |
0.1792 |
0.3220 |
| 1.8 |
1.9193 |
1.1684 |
0.3233 |
0.0567 |
0.0392 |
0.0491 |
0.0664 |
0.0906 |
0.1566 |
0.2834 |
| 1.9 |
1.9368 |
1.2153 |
0.3593 |
0.0624 |
0.0422 |
0.0487 |
0.0618 |
0.0913 |
0.1409 |
0.2337 |
| 2 |
1.9394 |
1.2699 |
0.3798 |
0.0676 |
0.0351 |
0.0474 |
0.0570 |
0.0941 |
0.1304 |
0.2186 |
| 2.1 |
1.9387 |
1.3083 |
0.4078 |
0.0698 |
0.0383 |
0.0426 |
0.0558 |
0.0873 |
0.1269 |
0.2084 |
| 2.2 |
1.9556 |
1.3326 |
0.4409 |
0.0796 |
0.0422 |
0.0419 |
0.0537 |
0.0833 |
0.1194 |
0.2091 |
| 2.3 |
1.9708 |
1.3666 |
0.4536 |
0.0799 |
0.0389 |
0.0456 |
0.0547 |
0.0849 |
0.1225 |
0.1971 |
| 2.4 |
1.9745 |
1.4162 |
0.4708 |
0.0810 |
0.0439 |
0.0419 |
0.0613 |
0.0858 |
0.1230 |
0.2088 |
| 2.5 |
1.9865 |
1.4251 |
0.4783 |
0.0784 |
0.0402 |
0.0427 |
0.0579 |
0.0836 |
0.1192 |
0.2110 |
| 2.6 |
1.9967 |
1.4305 |
0.4834 |
0.0826 |
0.0414 |
0.0391 |
0.0551 |
0.0816 |
0.1240 |
0.2156 |
| 2.7 |
1.9920 |
1.4437 |
0.4868 |
0.0840 |
0.0406 |
0.0440 |
0.0591 |
0.0933 |
0.1364 |
0.2442 |
| 2.8 |
1.9889 |
1.4728 |
0.4857 |
0.0805 |
0.0505 |
0.0420 |
0.0591 |
0.0974 |
0.1492 |
0.2658 |
| 2.9 |
1.9868 |
1.4837 |
0.4791 |
0.0819 |
0.0478 |
0.0461 |
0.0690 |
0.1089 |
0.1625 |
0.3037 |
| 3 |
1.9922 |
1.4876 |
0.4873 |
0.0838 |
0.0528 |
0.0505 |
0.0788 |
0.1166 |
0.1771 |
0.3461 |
可以看出,某些参数对应的EER低于4%,与公开发表的结果不相上下。特别的,最小EER为0.0351%(![]() ),低于文献[8]中的0.0379%,文献[9]中的0.038%,以及文献[10]中的0.0388%。
),低于文献[8]中的0.0379%,文献[9]中的0.038%,以及文献[10]中的0.0388%。
参考文献
[1] Adams Wai-Kin Kong, David Zhang. “CompetitiveCoding Scheme for Palmprint Verification”, Proceedings of the 17thInternational Conference on Pattern Recognition, pp. 520-523, 2004.
[2] David Zhang, Wangmeng Zuo, Feng Yue. “A Comparative Study of Palmprint RecognitionAlgorithms”,ACM Computing Surveys, vol.44, no. 1, Article 2, 2012.
[3] Adams Wai-Kin Kong, David Zhang. “ASurvey of Palmprint Recognition”,PatternRecognition, vol. 42, no. 7, pp. 1408-1418, 2009.
[4] PolyU Palmprint database,http://www.comp.polyu.edu.hk/~biometrics/
[5] I Ketut Gede Darma Putra, Erdiawan.“High Performance Palmprint Identification System Based On Two DimensionalGabor”,TELKOMNIKA, vol. 8, no. 3,pp. 309-318, 2010.
[6] Slobodan Ribarić,Marija Marčetić. “PersonalRecognition Based on the Gabor Features of Colour Palmprint Images”,Proceedings of the 35th InternationalConvention on MIPRO, pp. 967-972, 2012.
[7] Adams Wai-Kin Kong.Palmprint Identification Based onGeneralization of Iriscode, Ph. D. dissertation, Waterloo University, Canada,2007.
[8] Zhenhua Guo, David Zhang, LeiZhang, Wangmeng Zuo. “Palmprint Verification Using Binary Orientation Co-occurrenceVector”,Pattern Recognition Letters,vol. 30, no. 13, pp. 1219-1227, 2009.
[9] Wangmeng Zuo, Feng Yue, DavidZhang. “On Accurate Orientation Extraction and Appropriate Distance Measure forLow-resolution Palmprint Recognition”,PatternRecognition, vol. 44, no. 4, pp. 964-972, 2011.
[10] Wei Li, Bob Zhang, Lei Zhang,Jingqi Yan. “Principal Line-Based Alignment Refinement for PalmprintRecognition”,IEEE Transactions onSystems, Man, and Cybernetics, Part C: Applications and Reviews, vol. 42,no. 6, pp. 1491-1499, 2012.