机器学习之-支持向量机SVM原理

支持向量机

支持向量机（support vector machine，简称SVM）是一种二分类模型，它的基本模型是在特征空间上的间隔最大化的线性分类器，其学习模型的策略是间隔最大化，可转化为一个求解凸二次规划的最优化问题。训练后的线性分类器模型不仅保证了每个实例的预测类别准确性，而且还提高了每个实例的预测类别的置信度，从而增强了分类器模型的泛化能力。

支持向量机支持的由简至繁的模型：

1. 线性可分支持向量机：当训练数据线性可分时，通过硬间隔最大化，学习一个线性分类器，即线性可分支持向量机。
2. 线性支持向量机：当大部分训练数据线性可分，只有极少数数据不可分时，可通过软间隔最大化，学习一个线性分类器，即线性支持向量机。
3. 非线性支持向量机：当训练数据线性不可分时，通过使用核技巧及软间隔最大化，学习一个非线性支持向量机。

一、线性可分支持向量机

给定一个特征空间上的训练数据集$$T=\left\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\right\}$$其中，$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1，-1\right\},i=1,2,...,N,x_i$为第$i$个实例，$y_i$为$x_i$的类标记，当$y_i=+1$时，$x_i$为正例；当$y_i=-1$时，$x_i$为负例。假设训练数据集是线性可分的。学习的目标是在特征空间中找到一个分离超平面，能将所有实例划分到正确的类别中。分离的超平面模型是$wx+b=0$，模型参数是法向量$w$和截距$b$。分离超平面将特征空间划分为两类，一个是正类，另一个是负类。

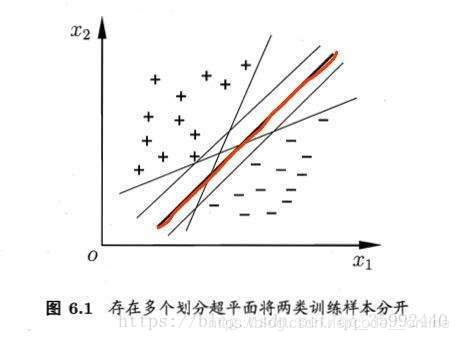
然而，当训练数据集线性可分时，存在无穷个分类超平面可将两类数据正确分开。虽然这些分类器保证了实例的正确分类，但是每个模型的泛化能力是有所差异的。为了保证实例以最大可能性的置信度进行预测分类，线性可分支持向量机利用间隔最大化来求解最优分离超平面。这个最优超平面是唯一的。

那么，问题来了，怎么确定这个最优超平面呢？

一般来说，一个点距离分离超平面越远，则表明这个分类预测准确度越大。在超平面$wx+b=0$确定的情况下，$|wx+b|$表示这个点$x$距离超平面的远近，而$wx+b$的符号与类标记$y$的符号是否一致能表示分类是否正确。所以可用$y(wx+b)$来表示分类的正确性及确定度，这就是函数间隔。实例$x_i$距离超平面的函数间隔可用$y_i(w{x}_i+b)$来表示。但是当成比例的改变$w,b$，超平面没有发生改变，但函数间隔也成比例的改变。因此，需要做规范化处理，即除以法向量$w$的模：$\frac{y_i(w{x}_i+b)}{||w||}$，这就是几何间隔。通过几何间隔度量实例到超平面的距离以及分类正确性。

1.1 间隔最大化

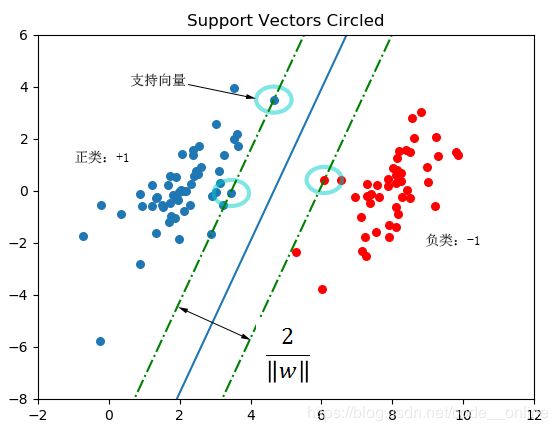
支持向量机学习的基本思想是求解能够正确划分数据集并且几何间隔最大的分离超平面。此时，发现有两个临界面$w^{T}x+b=1$和$w^{T}x+b=-1$。$w^{T}x+b=1$是类标记为1的临界面。当类别为1的实例，其满足$w^T{x}_i+b\ge 1$，而类别为-1的实例，其满足$w^T{x}_i+b\le -1$，因此，实例是否正确分类可依据$y_i(w^T{x}_i+b)\ge 1$这个条件来判定。为了使得分类置信度最大，需要保证两个临界面之间的距离尽可能的远，事实上相当于类别临界点到分离超平面的二倍几何间隔关系，即满足$\frac{2}{||w||}$最大化。其等价于$min\frac{1}{2}||w|{|}^2$，将其转化为一个凸二次规划的最优化问题：$$\underset{w,b}{\min }\frac{1}{2}||w|{|}^2$$$$s.t.y_i(w{x}_i+b)\ge 1,i=1,2,...,N$$

1.2 支持向量

在线性可分情况下，训练数据集的样本点中距离分离超平面最近的样本点实例称为支持向量，其满足$y_i(w{x}_i+b)=1$和对应的拉格朗日乘子${\alpha }_i>0$，即临界面上的实例点。

在训练分离超平面模型时，只有支持向量起作用，相对的，其他实例点并不起作用。当改变支持向量时，相应的分离超平面也将发生改变；如果改变除了支持向量的其他实例点，分离超平面不会发生改变。因此，支持向量决定了分离超平面，这种模型被称为支持向量机。支持向量个数一般很少，所以，支持向量机由很少的“重要的”训练样本确定。

1.3 对偶算法

为了求解线性可分支持向量机的最优化问题，将它作为原始最优化问题，应用拉格朗日对偶性，通过求解对偶问题得到原始问题的最优解，这就是线性可分支持向量机的对偶算法。优点是对偶问题通常更容易求解，而且还可以引入核函数，进而推广到非线性分类问题。（具体算法可参阅统计学习方法附录C）
通过拉格朗日函数将一个约束的凸优化问题转化为非约束的优化问题，为此，为每一个实例的不等式约束引入拉格朗日乘子${\alpha }_i\ge 0,i=1,2,...,N$，拉格朗日函数如下：$$L(w,b,\alpha )=\frac{1}{2}||w|{|}^2-\sum _{i=1}^N{\alpha }_i{y}_i(w{x}_i+b)+\sum _{i=1}^N{\alpha }_i$$其中，$\alpha =({\alpha }_1,{\alpha }_2,...,{\alpha }_N{)}^T$为拉格朗日向量。那么，将原始问题的最优解 $w,b$转化为拉格朗日函数的极小极大问题，即

$$\underset{w,b}{\min }\underset{\alpha }{\max }L(w,b,\alpha )$$根据拉格朗日对偶性，原始问题的对偶问题是极大极小问题：$$\underset{\alpha }{\max }\underset{w,b}{\min }L(w,b,\alpha )$$为了得到对偶问题的解，需要先求$L(w,b,\alpha )$对$w,b$的极小，再求对$\alpha$的极大。

• ${\min }_{w,b}L(w,b,\alpha )$
  将拉格朗日函数$L(w,b,\alpha )$分别对$w,b$求偏导数并令其为0。$$\frac{\partial L(w,b,\alpha )}{w}=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0⟹w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i$$$$\frac{\partial L(w,b,\alpha )}{b}=-\sum _{i=1}^N{\alpha }_i{y}_i=0⟹\sum _{i=1}^N{\alpha }_i{y}_i=0$$
  再将其代入拉格朗日函数中，得到以下函数：$$\begin{array}{rl}L(w,b,\alpha )& =\frac{1}{2}||w|{|}^2-\sum _{i=1}^N{\alpha }_i{y}_i(w.x_i+b)+\sum _{i=1}^N{\alpha }_i\\ & =\frac{1}{2}||w|{|}^2-w\sum _{i=1}^N{\alpha }_i{y}_i{x}_i-b\sum _{i=1}^N{\alpha }_i{y}_i+\sum _{i=1}^N{\alpha }_i\\ & =-\frac{1}{2}||w|{|}^2+\sum _{i=1}^N{\alpha }_i=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩+\sum _{i=1}^N{\alpha }_i\end{array}$$即$$\underset{w,b}{\min }L(w,b,\alpha )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩+\sum _{i=1}^N{\alpha }_i$$
• 求${\min }_{w,b}L(w,b,\alpha )$对$\alpha$的极大，即对偶问题：$$\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩+\sum _{i=1}^N{\alpha }_i$$$$\begin{gathered} s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ {\alpha }_i\ge 0,i=1,2,...,N \end{gathered}$$等价于以下最优化问题：$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩-\sum _{i=1}^N{\alpha }_i$$$$\begin{gathered} s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ {\alpha }_i\ge 0,i=1,2,...,N \end{gathered}$$
  对于线性可分训练数据集，对偶优化问题可利用SMO算法（可参考SMO博客）求解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$，进而求解$w^{\ast }={\sum }_{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$，$b^{\ast }$可通过选择一个非零的${\alpha }_i>0$，将其对应的$(x_i,y_i)$代入到$y_i(w{x}_i+b)=1$求解$b^{\ast }=y_i-{\sum }_{j=1}^N{\alpha }_j^{\ast }{y}_j⟨x_i,x_j⟩$，最终得到分离超平面及分类决策函数。
  分离超平面：$$\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x,x_i⟩+b^{\ast }=0$$
  分类决策函数：$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x,x_i⟩+b^{\ast })$$

1.4 线性可分支持向量机学习算法

输入：线性可分训练集$T=\left\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\right\}$，其中，$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1，-1\right\},i=1,2,...,N$
输出：分离超平面和分类决策函数

• 构造并求解约束最优化问题$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩-\sum _{i=1}^N{\alpha }_i$$$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$ $${\alpha }_i\ge 0,i=1,2,...,N$$求最优解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$
• 计算$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$选择${\alpha }^{\ast }$的一个正分量${\alpha }_j^{\ast }>0$，计算$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x_i,x_j⟩$$
• 求分离超平面$$\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x,x_i⟩+b^{\ast }=0$$分类决策函数$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x,x_i⟩+b^{\ast })$$
  在线性可分支持向量机中，$w^{\ast }$和$b^{\ast }$只依赖于训练数据对应的${\alpha }_i^{\ast }>0$的样本点$(x_i,y_i)$，而其他样本点对$w^{\ast }$和$b^{\ast }$没有影响。这些对应的${\alpha }_i^{\ast }>0$的样本点$(x_i,y_i)$称为支持向量。

给定线性可分训练数据集，通过硬间隔最大化求解相应的凸二次规划问题学习得到的分离超平面为线性可分支持向量机。

二、线性支持向量机

对于理想情况下，训练数据集是线性可分的，但是在现实问题中的训练数据集存在少量的噪声点或者特异点，这些特殊点导致线性不可分。为了学习分类器模型，将硬间隔最大化的学习策略更改为软间隔最大化，使得分类器模型允许一些噪声点的干扰。为了解决不满足$y_i(w{x}_i+b)\ge 1$这个约束条件的样本点$(x_i,y_i)$，可以对每个样本点$(x_i,y_i)$引入一个松弛变量${\xi }_i\ge 0$，使函数间隔加上松弛变量大于等于1，即$$y_i(w{x}_i+b)+{\xi }_i\ge 1$$为了防止松弛变量过大，对松弛变量引入了惩罚参数C，目标函数变为：$$\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$$C>0$为惩罚参数，C值越大，表明对误分类的${\xi }_i$惩罚力度越大；C值越小，则对误分类的${\xi }_i$惩罚力度越小。最小化目标函数的含义是使$\frac{1}{2}||w|{|}^2$最小化的同时还要保证误分类的个数和对应的松弛变量尽量小，C是调和这两者之间的系数。
软间隔最大化的凸优化问题：$$\underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$$$s.t.y_i(w{x}_i+b)+{\xi }_i\ge 1,i=1,2,...,N$$$${\xi }_i\ge 0,i=1,2,...,N$$
原始问题的拉格朗日函数，即
$$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i(y_i(w{x}_i+b)-1+{\xi }_i)-\sum _{i=1}^N{\mu }_i{\xi }_i,{\alpha }_i\ge 0,{\mu }_i\ge 0$$与线性可分支持向量机求解步骤相同，求$L(w,b,\xi ,\alpha ,\mu )$对$w,b,\xi$的极小$$\begin{array}{rl}& \frac{\partial L(w,b,\xi ,\alpha ,\mu )}{w}=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0⟹w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i\\ & \frac{\partial L(w,b,\xi ,\alpha ,\mu )}{b}=-\sum _{i=1}^N{\alpha }_i{y}_i=0⟹\sum _{i=1}^N{\alpha }_i{y}_i=0\\ & \frac{\partial L(w,b,\xi ,\alpha ,\mu )}{{\xi }_i}=C-{\alpha }_i-{\mu }_i=0\end{array}$$将其代入到拉格朗日函数得到如下函数：$$\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩+\sum _{i=1}^N{\alpha }_i$$再对${\min }_{w,b,\xi }L(w,b,\xi ,\alpha ,\mu )$求$\alpha$的极大，得到对偶问题：$$\underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩+\sum _{i=1}^N{\alpha }_i$$$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$$$C-{\alpha }_i-{\mu }_i=0$$$${\alpha }_i\ge 0,i=1,2,...,N$$$${\mu }_i\ge 0,i=1,2,...,N$$

等价于$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩-\sum _{i=1}^N{\alpha }_i$$$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$$$0\le {\alpha }_i\le C,i=1,2,...,N$$同理，对于满足KKT条件的对偶问题，通过SMO算法求解对偶问题的解，从而得到原始问题的解，最终确定分离超平面及分类决策函数。

2.1 线性支持向量机学习算法

输入：线性可分训练集$T=\left\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\right\}$，其中，$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1，-1\right\},i=1,2,...,N$
输出：分离超平面和分类决策函数

• 选择惩罚参数C>0，构造并求解凸二次规划问题$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j⟨x_i,x_j⟩-\sum _{i=1}^N{\alpha }_i$$$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$ $$0\le {\alpha }_i\le C,i=1,2,...,N$$求最优解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$
• 计算$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$选择${\alpha }^{\ast }$的一个正分量$0<{\alpha }_j^{\ast }<C$，计算$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x_i,x_j⟩$$
• 求分离超平面$$\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x,x_i⟩+b^{\ast }=0$$分类决策函数$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨x,x_i⟩+b^{\ast })$$

2.2 支持向量

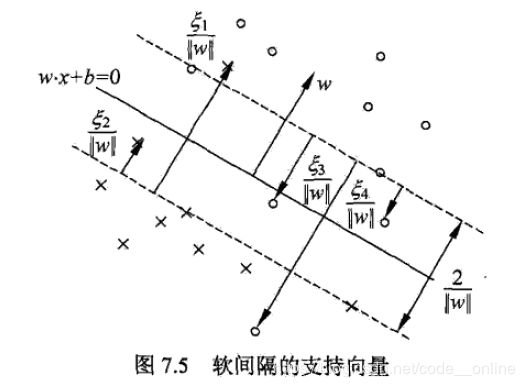
分离超平面由实线表示，间隔边界由虚线表示，正例点由“o”表示，负例点由“x”表示。实例$x_i$到间隔边界的距离为$\frac{{\xi }_i}{||w||}$

软间隔的支持向量$x_i$可能在间隔边界上，或者在间隔边界与分离超平面之间，或者在分离超平面误分的一侧。若${\alpha }_i<C$,则${\xi }_i=0$，支持向量$x_i$在间隔边界上；若${\alpha }_i=C,0<{\xi }_i<1$，则分类正确，$x_i$在间隔边界与分离超平面之间；若${\alpha }_i=C,{\xi }_i=1$，则$x_i$在分离超平面上；若${\alpha }_i=C,{\xi }_i>1$，则$x_i$在分离超平面误分的另一侧；

对于给定的线性不可分的训练数据集，通过软间隔最大化求解的凸二次规划问题，得到的分离超平面是线性支持向量机。

三、非线性支持向量机

3.1 核技巧

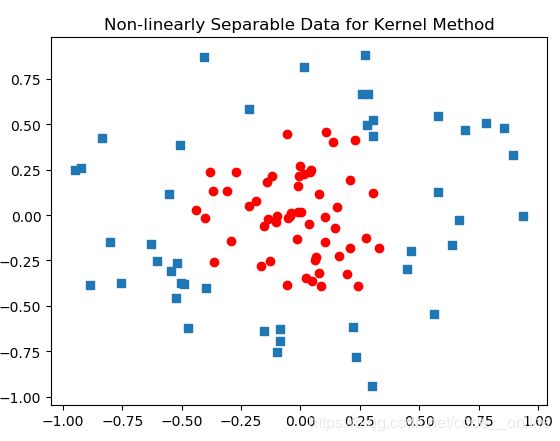
非线性分类问题一般无法直接用线性分类器来进行有效分类，只能利用非线性模型才能很好地进行分类。例如，如下图是样本的分布，在该空间内不存在一个线性分类器进行分类，但是存在一个超曲面可将正负例分类。

为了使用线性分类问题的解决方法，将该特征空间的实例映射到另一特征空间内，使得实例点线性可分，其采取的方法是进行一个非线性变化，把非线性问题变换为线性问题，再通过解决变换后的线性问题的方法求解原始的非线性问题。

用线性分类方法求解非线性分类问题分为两步：首先使用一个非线性变换将原始空间的数据映射到新的空间，然后，在新空间里用线性分类学习方法从训练数据中学习分类模型。

那么，问题来了，如何找到这种特征空间呢？如何确定原始空间到新特征空间的映射函数呢？

核技巧应用到支持向量机，其基本思想是通过一个非线性变换将输入空间映射到一个特征空间，使得在输入空间中的超曲面模型对应特征空间的超平面模型，这样，分类问题可通过在特征空间求解线性支持向量机。

事实上，根本不需要大费周章的求解新特征空间及相应的映射函数。由于原始空间的超平面模型与新空间的超平面模型是一一对应的关系，原始空间里超曲面模型中的$⟨x,z⟩$对应着新空间里超平面的$⟨\varphi (x),\varphi (z)⟩$，只需要计算$⟨\varphi (x),\varphi (z)⟩$即可得到实例的预测类别。但是，计算$⟨\varphi (x),\varphi (z)⟩$相对比较复杂。因此，引入了核函数$K(x,z)$，其等价于$⟨\varphi (x),\varphi (z)⟩$，节省了求解新特征空间及对应的映射函数所带来的开销，简化了模型的求解过程。

核函数：设$\mathcal{X}$是输入空间，$\mathcal{H}$是特征空间，如果存在一个从$\mathcal{X}$到$\mathcal{H}$的映射$$\varphi (x):\mathcal{X}\to \mathcal{H}$$使得所有$x,z\in \mathcal{X}$，满足$K(x,z)$满足条件$$K(x,z)=\varphi (x).\varphi (z)$$$K(x,z)$为核函数，$\varphi (x)$为映射函数，$\varphi (x).\varphi (z)$为$\varphi (x)$与$\varphi (z)$的乘积。

使用核技巧的对偶问题的目标函数变为：$$\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i$$相应的分类决策函数：$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i⟨\varphi (x_i),\varphi (x_j)⟩+b^{\ast })=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)+b^{\ast })$$
在核函数$K(x,z)$给定的条件下，利用解线性分类问题的方法求解非线性分类问题的支持向量机。学习是隐式地在特征空间进行，不需要显示低定义特征空间与映射函数，这样的技巧为核技巧，巧妙地利用线性分类学习方法与核函数解决非线性分类问题。

3.2 常用的核函数

• 线性核函数（linear）$$K(x,z)=⟨x,z⟩$$
• 多项式核函数（poly）$$K(x,z)=(\gamma ⟨x,z⟩+r{)}^d$$
• 高斯核函数（rbf）$$K(x,z)=exp(-\gamma ||x-z|{|}^2)$$
• sigmoid核函数 $$tanh(\gamma ⟨x,z⟩+r)$$

3.3 非线性支持向量机学习算法

输入：训练集$T=\left\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\right\}$，其中，$x_i\in \mathcal{X}=R^n,y_i\in \mathcal{Y}=\left\{+1，-1\right\},i=1,2,...,N$
输出：分类决策函数

• 选择适当的核函数$K(x,z)$和适当的惩罚参数C>0，构造并求解最优化问题$$\underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_{j}K(x_i,x_j)-\sum _{i=1}^N{\alpha }_i$$$$s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0$$ $$0\le {\alpha }_i\le C,i=1,2,...,N$$求最优解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$
• 计算$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$选择${\alpha }^{\ast }$的一个正分量$0<{\alpha }_j^{\ast }<C$，计算$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x_i,x_j)$$
• 分类决策函数$$f(x)=sign(\sum _{i=1}^N{\alpha }_i^{\ast }{y}_{i}K(x,x_i)+b^{\ast })$$

从非线性分类训练集，通过核函数和软间隔最大化，学习得到的分类决策函数为非线性支持向量。

四、SVM参数

参数	含义
C	float类型，默认值为1.0，错误实例的惩罚参数
kernel	默认核函数为rbf，可选项为“linear”，“poly”，“rbf”’，“sigmoid”, “precomputed“等等
degree	默认为3.0，只有poly核函数有这个参数，其他核函数没有
gamma	‘rbf’, ‘poly’ and 'sigmoid’核函数的核系数。默认为auto，如果默认值，则表示为1/n_features
coef0	只有’poly’ and 'sigmoid’核函数有这个参数，用$r$表示，默认为0.0
probability	boolean类型，表示是否启用概率评估
shrinking	Boolean类型，默认为True，表示是否使用缩减启发式
tol	默认为1e-3，表示标准终止的容忍值
cache_size	指定核缓存的大小
class_weight	类别的权重，字典形式传递。设置第几类的参数C为weight*C
verbose	默认为False，是否支持冗余输出
max_iter	默认为-1，表示最大迭代次数。-1为无限制
decision_function_shape	‘ovo’：one vs one, ‘ovr’：one vs rest, default=‘ovr’
random_state	数据洗牌时的种子值，int值

五、SVM实战

import numpy as np
import pandas as pd
from sklearn.svm import SVC
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split

# 加载数据
def load_data():
    iris = load_iris()
    df_iris = pd.DataFrame(iris.data, columns=iris.feature_names)
    df_iris['label'] = iris.target
    df_iris.columns = ['sepal length', 'sepal width', 'petal length', 'petal width', 'label']
    df_data = np.array(df_iris.iloc[:100, :])
    for i in range(len(df_data)):
        if df_data[i, -1] == 0:
            df_data[i, -1] = -1
    del df_iris
    return df_data[:, :-1], df_data[:, -1]


X, y = load_data()
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=2019)


class SVM(object):
    def __init__(self, max_iter=100, kernel='linear', C=1.0):
        self.max_iter = max_iter
        self.kernel = kernel
        self.C = C   # 松弛变量
        self.b = 0.0  # 偏置b

    # 初始化参数
    def _init_args(self, data, label):
        self.instances, self.features = data.shape  # （样本实例数量，特征数量）
        self.X = data
        self.y = label
        self.alpha = np.zeros(self.instances)  # 实例对应的拉格朗日乘子
        self.E = [self._E(i) for i in range(self.instances)]  # 实例对应的误差

    # 计算误差
    def _E(self, i):
        return self.gxi(i) - self.y[i]

    # 核函数
    def _kernel(self, xi, xj):
        if self.kernel == 'linear':
            return sum([xi[k] * xj[k] for k in range(self.features)])
        if self.kernel == 'poly':
            return (sum([xi[k] * xj[k] for k in range(self.features)]) + 1) ** 2
        return 0

    # 样本的预测值
    def gxi(self, i):
        r = self.b
        for j in range(self.instances):
            r += self.alpha[j] * self.y[j] * self._kernel(self.X[i], self.X[j])
        return r

    # KKT条件
    def KKT(self, i):
        y_g = self.y[i] * self.gxi(i)
        if self.alpha[i] == 0:
            return y_g >= 1
        elif 0 < self.alpha[i] < self.C:
            return y_g == 1
        else:
            return y_g <= 1

    # 选择合适的i，j
    def init_alphas(self):
        support_vectors_indexs = [i for i in range(self.instances) if 0 < self.alpha[i] < self.C]
        non_safity_list = [i for i in range(self.instances) if i not in support_vectors_indexs]
        support_vectors_indexs.extend(non_safity_list)

        for i in support_vectors_indexs:
            if self.KKT(i):
                continue
            Ei = self.E[i]
            if Ei >= 0:
                j = min(range(self.instances), key=lambda x: self.E[x])
            else:
                j = max(range(self.instances), key=lambda x: self.E[x])
        return i, j

    # 范围约束的拉格朗日乘子
    def _compare(self, L, H, _alpha):
        if _alpha >= H:
            return H
        elif _alpha <= L:
            return L
        else:
            return _alpha

    # 训练模型
    def fit(self, data, label):
        self._init_args(data, label)

        for iter in range(self.max_iter):
            i, j = self.init_alphas()
            Ei, Ej = self.E[i], self.E[j]

            if self.y[i] == self.y[j]:
                L = max(0, self.alpha[j] + self.alpha[i] - self.C)
                H = min(self.C, self.alpha[j] + self.alpha[i])
            else:
                L = max(0, self.alpha[j] - self.alpha[i])
                H = min(self.C, self.C + self.alpha[j] - self.alpha[i])

            eta = self._kernel(self.X[i], self.X[i]) + self._kernel(self.X[j], self.X[j]) \
                  - 2 * self._kernel(self.X[i], self.X[j])
            if eta <= 0:
                continue

            alphaj_new_unc = self.alpha[j] + self.y[j] * (Ei - Ej) / eta

            alphaj_new = self._compare(L, H, alphaj_new_unc)
            alphai_new = self.alpha[i] + self.y[i] * self.y[j] * (self.alpha[j] - alphaj_new)

            # 更新偏置b
            b1_new = -self.E[i] - self.y[i] * self._kernel(self.X[i], self.X[i]) * (alphai_new - self.alpha[i]) - \
                     self.y[j] * self._kernel(self.X[j], self.X[i]) * (alphaj_new - self.alpha[j]) + self.b
            b2_new = -self.E[j] - self.y[i] * self._kernel(self.X[i], self.X[j]) * (alphai_new - self.alpha[i]) - \
                     self.y[j] * self._kernel(self.X[j], self.X[j]) * (alphaj_new - self.alpha[j]) + self.b

            if alphai_new > 0 and alphai_new < self.C:
                b_new = b1_new
            elif alphaj_new > 0 and alphaj_new < self.C:
                b_new = b2_new
            else:
                b_new = (b1_new + b2_new) / 2

            self.alpha[i] = alphai_new
            self.alpha[j] = alphaj_new
            self.b = b_new

            self.E[i] = self._E(i)
            self.E[j] = self._E(j)
        print('train done...')

    def predict(self, data):
        r = self.b
        for i in range(self.instances):
            r += self.alpha[i] * self.y[i] * self._kernel(self.X[i], data)
        return 1 if r > 0 else -1

    def score(self, X_test, y_test):
        pred_cnt = sum(1 for i in range(len(X_test)) if self.predict(X_test[i]) == y_test[i])
        return pred_cnt / len(X_test)


svm = SVM()
svm.fit(X_train, y_train)
print("The score of custom svm model's prediction is :",svm.score(X_test, y_test))

clf = SVC(gamma='auto')
clf.fit(X_train,y_train)
print("The score of built-in SVC model's prediction is:",clf.score(X_test,y_test))

The score of custom svm model's prediction is: 0.95
The score of built-in SVC model's prediction is: 1.0

参考文献

• 李航 《统计学习方法》
• 周志华 《机器学习》
• scikit-learn官方文档