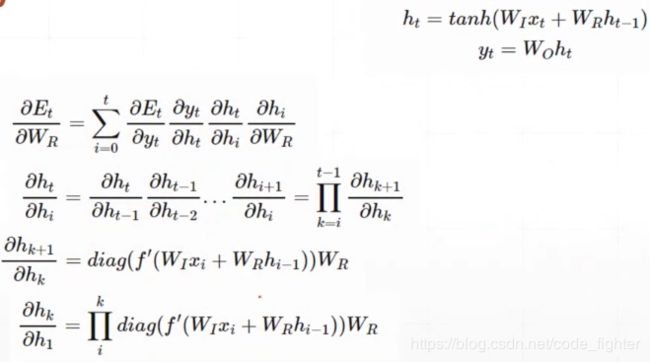pytorch学习笔记7--循环神经网络、GAN

循环神经网络

序列的表示方法

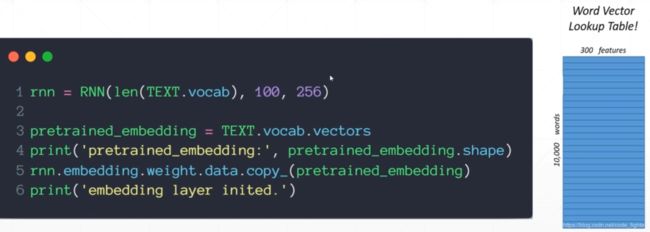
1. pytorch 中 string的表示方法：word embedding [seq_len,feature_len]、[words,word_vec]、one-hot…
   eg：[5,1],[5,100]

2. batch

   1. [word num, b, word_vec]
   2. [b,word num, word vec]

3. word2vec v.s. Glove

word_to_ix = {"hello":0,"world":1}
lookup_tensor = torch.tensor([word_to_ix["hello"]],dtype=torch.long)

embeds = nn.Embedding(2,5)
hello_embed = embeds(lookup_tensor)
print(hello_embed)
:tensor([[0.6614,0.2669,0.0617,0.6213,-0.4519]],grad_fn=<EmbeddingBackward>)

from torchnlp word_to_vector import Glove
vectors = GloVe()

vectors['hello']
:-1.7494
:0.6242
:...
:-0.6202
:2.0928
:[torch.FloatTensor of size 100]

RNN Layer的使用

nn.RNN

rnn = nn.RNN(input_size=100,hidden_size=20,num_layers=4)
print(rnn)
x = torch.randn(10,3,100)
out,h = rnn(x)
print(out.shape,h.shape)
:torch.Size([10,3,20])  torch.Size([4,3,20])

nn.RNNCell

cell1 = nn.RNNCell(100,20)
h1 = torch.zeros(3,20)
for xt in x:
    h1 = cell1(xt,h1)
print(h1.shape)
:torch.Size([3,20])

cell1 = nn.RNNCell(100,30)
cell2 = nn.RNNCell(30,20)

h1 = torch.zeros(3,30)
h2 = torch.zeros(3,20)

for xt in x:
    h1 = cell1(xt,h1)
    h2 = cell2(h1,h2)

print(h2.shape)
:torch.Size([3,20])

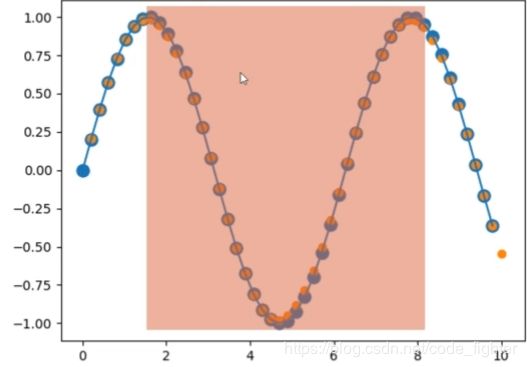
预测sin(x)曲线

start = np.random.radint(3,size=1)[0]
time_steps = np.linspace(start,start+10,num_time_steps)
data = np.sin(time_steps)
data = data.reshape(num_time_steps,1)
x = torch.tensor(data[:-1]).float().view(1,num_time_steps -1,1)
y = torch.tensor(data[1:]).float().view(1,num_time_steps -1,1)

class Net(nn.Module):
    def __init__(self,):
        super(Net,self).__init__()
        self.rnn = nn.RNN(
            input_size = input_size,
            hidden_size = hidden_size,
            num_layers = 1,
            batch_first = True,
        )
        self.linear = nn.Linear(hidden_size,output_size)
        
    def forward(self,x,hidden_prew):
        out,hidden_prev = self.rnn(x,hidden_prev)
        
        out = out.view(-1,hidden_size)
        out = self.linear(out)
        out = out.unsqueeze(dim=0)
        return out, hidden_prev

train

model = Net()
criterion = nn.MSELoss()
optimizer = optim.Adam(model.parameters(),lr)

hidden_prev = torch.zeros(1,1,hidden_size)
for iter in range(6000):
    start = np.random.randint(10,size=1)[0]
    time_steps = np.linspace(start,start+10,num_time_steps)
    data = np.sin(time_steps)
    data = data.reshape(num_time_steps,1)
    x = torch.tensor(data[:-1]).float().view(1,num_time_steps-1,1)
    y=torch.tensor(data[1:]).float().view(1,num_time_steps-1,1)
    output,hidden_prev = model(x,hidden_prev)
    hidden_prev = hidden_prev.detach()
    
    loss = criterion(output,y)
    model.zero_grad()
    loss.backward()
    optimizer.step()
    
    if iter %100 == 0:
        print("Iteration :{ }  loss { }".format(iter,loss.item()))

predict

predictions = []
input = x[:,0,:]
for _ in range(x.shape[1])
    input = input.view(1,1,1)
    (pred,hidden_prev) = model(input,hidden_prev)
    input = pred
    predictions.append(pred.detach().numpy().ravel()[0])

梯度弥散和梯度爆炸

gradient clipping

loss = criterion(output,y)
model.zero_grad()
loss.backward()
for p in model.parameters():
    print(p.grad.norm())
    torch.nn.utils.clip_grad_norm(p,10)# 把梯度clipping到0~10 的范围
optimizer.step()

gradient vanishing

梯度长时间得不到更新
LSTM解决梯度弥散

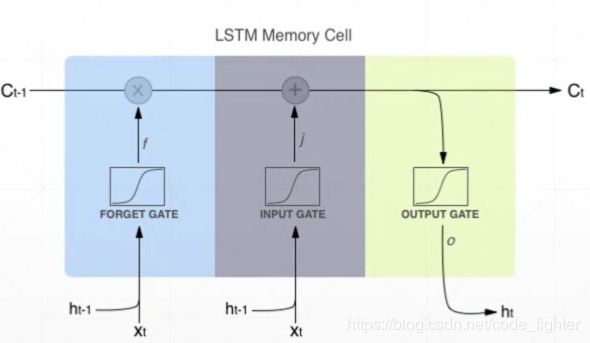
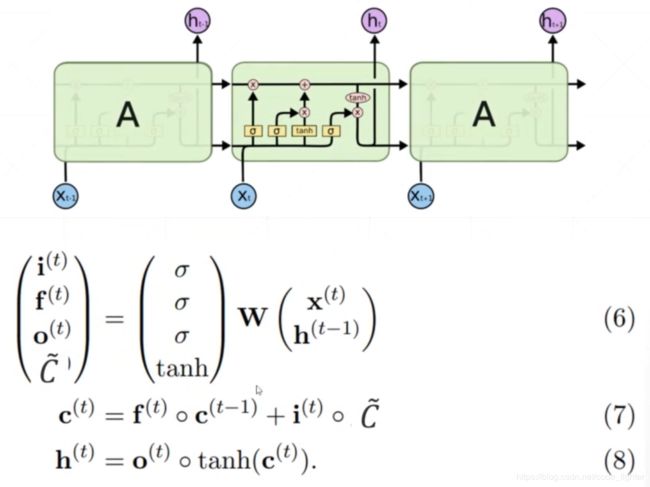
LSTM 的使用

lstm = nn.LSTM(input_size=100, hidden_size=20,num_layers=4)
print(lstm)
x = torch.randn(10,3,100)
out,(h,c) = lstm(x)
print(out.shape,h.shape,c.shape)

: torch.Size([10,3,20]) torch.Size([4,3,20]) torch.Size([4,3,20])

LSTMCell 的使用

print('one layer lstm')
cell = nn.LSTMCell(input_size=100,hidden_size=20)
h = torch.zeros(3,20)
c = torch.zeros(3,20)
for xt in x :
    h,c = cell(xt,[h,c])

print(h.shape,c.shape)

: torch.Size([3,20]) torch.Size([3,20])

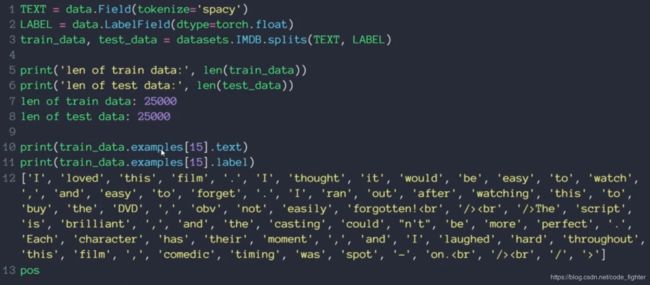
情感分类实战

class RNN(nn.Module):
	def __init__(self,vocab_size,embedding_dim,hidden_dim):
		super(RNN,self).__init__()
		# [0-10001] =>[100]
		self.embedding = nn.Embedding(vocab_size,embedding_dim)
		#[100] => [256]
		self.rnn = nn.LSTM(embedding_dim,hidden_dim,num_layers=2,bidirectional=True,dropout=0.5)
		#[256*2] = > [1]
		self.fc = nn.Linear(hidden_dim*2,1)
		self.dropout = nn.Dropout(0.5)
	def forward(self,x):
		# [seq,b,1] => [seq,b,100]
		embedding = self.dropout(self.embedding(x))
		#output:[seq,b,hid_dim*2]
		#hidden/h: [num_layers*2,b,hid_dim]
		# cell/c: [num_layers*2,b,hid_dim]
		output,(hidden,cell) = self.rnn(embedding)
		# [num_layers*2,b,hid_dim] => 2 of [b,hid_dim] => []b,hid_dim*2]
		hidden = torch.cat([hidden[-2],hidden[-1]],dim=1)
		# [b,did_dim*2] => [b,1]
		hidden = self.dropout(hidden)
		out = self.fc(hidden)
		return out

def train(rnn,iterator,optimizer,criteon):
	avg_acc = []
	rnn.train()
	for i , batch in enumerate(iterator):
		# [seq,b] => [b,1] => [b]
		pred = rnn(batch.text).squeeze(1)
		loss = criteon(pred,batch.label)
		acc = binary_acc(pred,batch.label).item()
		avg_acc.append(acc)
		optimizer.zero_grad()
		loss.backward()
		optimizer.step()

def binary_acc(preds,y):
	preds = torch.round(torch.sigmoid(preds))
	correct = torch.eq(preds,y).float()
	acc = correct.sum()/len(correct)
	return acc

def eval(rnn,iterator,criteon):
	avg_acc = []
	rnn.eval()
	with torch.no_grad():
		for batch in iterator:
			# [b,1] =>[b]
			pred = rnn(batch.text).squeeze(1)
			loss = criteon(pred,batch.label)
			acc = binary_acc(pred,batch.label).item()
			avg_acc.append(acc)
	avg_acc = np.array(avg_acc).mean()
	print('>>test:',avg_acc)		

GAN

损失

$$mi{n}_{G}ma{x}_{D}L(D,G)=E_{x{p}_r(x)}[logD(x)]+E_{x{p}_z(z)}[log(1-D(G(z)))]=E_{x{p}_r(x)}[logD(x)]+E_{x{p}_g(x)}[log(1-D(x))]$$

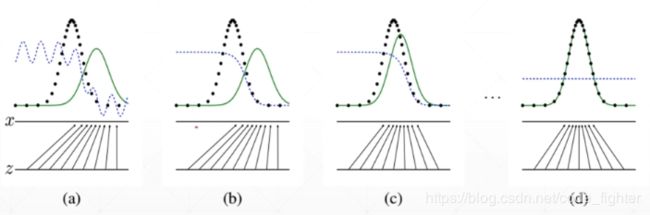
纳什均衡

1. where will D converge, given fixed G
   1. for G fixed ,the optimal discriminator D is $D_G^{\ast }(x)=\frac{P_{data}(x)}{P_{data}(x)+p_g(x)}$
   2. proof. the training criterion for the discriminator D, given any generator G, is to maximize the quantity V(G,D)
   3. $$V(G,D)={\int }_x{P}_{data}(x)log(D(x))dx+{\int }_z{P}_z(z)log(1-D(g(z)))dz={\int }_x{P}_{data}(x)log(D(x))+P_g(x)log(1-D(x))dx$$
   4. 因为G 是固定的，所以令$P_{data}(x)=A,P_g(x)=B$
   5. $$f(\tilde{x})=Alog\tilde{x}+blog(1-\tilde{x})$$
   6. 令$\frac{df(\tilde{x})}{d\tilde{x}}=A\frac{1}{ln10}\frac{1}{\tilde{x}}-B\frac{1}{ln10}\frac{1}{1-\tilde{x}}=\frac{1}{ln10}(\frac{A}{\tilde{x}}-\frac{B}{1-\tilde{x}})=\frac{1}{ln10}\frac{A-(A+B)\tilde{x}}{\tilde{x}(1-\tilde{x})}=0$
   7. 所以：$D^{\ast }(x)={\tilde{x}}^{\ast }=\frac{A}{A+B}=\frac{p_r(x)}{p_r(x)+p_g(x)}\in [0,1]$
2. KL Divergence vs. JS Divergence
   1. $D_{KL}(p||q)={\int }_{x}p(x)log\frac{p(x)}{q(x)}dx$
   2. $D_{JS}(p||q)=\frac{1}{2}{D}_{KL}(p||\frac{p+q}{2})+\frac{1}{2}{D}_{KL}(q||fracp+q2)$ 主要解决kl不对称的问题
3. where will G converge,after optimal D

$D_{JS}(P_r||P_g)=\frac{1}{2}{D}_{KL}(P_r||\frac{P_r+P_g}{2})+\frac{1}{2}{D}_{KL}(P_g||\frac{P_r+P_g}{2})$

$=\frac{1}{2}(log2+{\int }_x{P}_r(x)log\frac{P_r(x)}{P_r+P_g(x)})+\frac{1}{2}(log2+{\int }_x{P}_g(x)log(\frac{P_g(x)}{P_r+P_g(x)})dx$

$=\frac{1}{2}(log4+L(G,D^{\ast }))$
所以
$$L(G,D^{\ast })=2D_{JS}(P_r||P_g)-2log2$$
$D_{JS}(P_r||P_g)\ge 0$
$P_r=P_g$

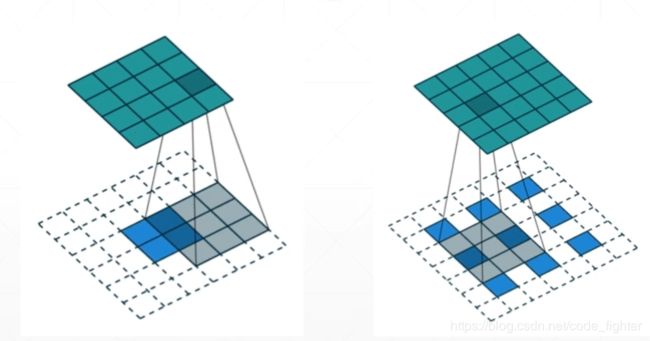
transposed convolution

WGAN 使用wassertein Distance 代替了Discriminator

GAN 实战

import numpy as np
import visdom
import random
from torch import nn, optim,autograd
import torch
from  matplotlib import pyplot as plt
h_dim = 400
batchsz = 512
viz = visdom.Visdom()

class Generator(nn.Module):
    def __init__(self):
        super(Generator,self).__init__()

        self.net = nn.Sequential(
            nn.Linear(2,h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim,h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim,h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim,2)
        )
    def forward(self, x):
        output = self.net(x)
        return output

class Discriminator(nn.Module):

    def __init__(self):
        super(Discriminator,self).__init__()

        self.net = nn.Sequential(
            nn.Linear(2,h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim,h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim,h_dim),
            nn.ReLU(True),
            nn.Linear(h_dim,1),
            nn.Sigmoid()

        )

    def forward(self, x):
        output = self.net(x)
        return output


def data_generator():
    scale = 2.
    centers = [(1,0),(-1,0),(0,1),(0,-1),(1./np.sqrt(2),1./np.sqrt(2)),
               (1./np.sqrt(2),-1./np.sqrt(2)),(-1./np.sqrt(2),1./np.sqrt(2))
               ,(-1./np.sqrt(2),-1./np.sqrt(2))]

    while True:
        dataset = []
        for i in range(batchsz):
            point = np.random.randn(2)*0.02
            center = random.choice(centers)

            point[0] += center[0]
            point[1] += center[1]
            dataset.append(point)

        dataset = np.array(dataset).astype(np.float32)
        dataset /= 1.414
        yield  dataset


def main():

    torch.manual_seed(23)
    np.random.seed(23)

    data_iter = data_generator()
    x = next(data_iter)

    G = Generator().cuda()
    D = Discriminator().cuda()
    optim_G = optim.Adam(G.parameters(),lr=5e-4,betas=(0.5,0.9))
    optim_D = optim.Adam(D.parameters(),lr=5e-4,betas=(0.5,0.9))

    for epoch in range(50000):
        for _ in range(5):
            # train on real data
            x = next(data_iter)
            x = torch.from_numpy(x).cuda()
            predr = D(x)
            # max predr,min lossr
            lossr = predr.mean()

            z = torch.randn(batchsz,2).cuda()
            xf = G(z).detach()
            predf = D(xf)
            lossf = predf.mean()

            # aggregate all
            loss_D = lossr + lossf

            # optimize
            optim_D.zero_grad()
            loss_D.backward()
            optim_D.step()

        # 2 train Generator
        z = torch.randn(batchsz,2).cuda()
        xf = G(z)
        predf = D(xf)
        loss_G = predf.mean()

        # optimize
        optim_G.zero_grad()
        loss_G.backward()
        optim_G.step()