数学建模（六） 主成分分析，聚类分析，对策论，马氏链

全并到一起写是因为我只想写十篇。

1.主成分分析

PCA！！！
主成分分析（Principal Component Analysis， PCA），将多个变量通过线性变换以选出较少个数重要变量的一种多元统计分析方法。
主成分：由原始指标综合形成的几个新指标。依据主成分所含信息量的大小称为第一主成分，第二主成分等等。由讨论多个指标降为少数几个综合指标的过程在
数学上就叫做降维。主成分分析通常的做法是，寻求原指标的线性组合Fi。
同样可以用SPSS作，过程不能略，因为略掉这部分就讲完了，粘几个表格吧：
数据：



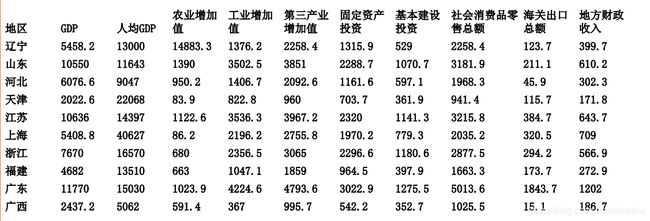
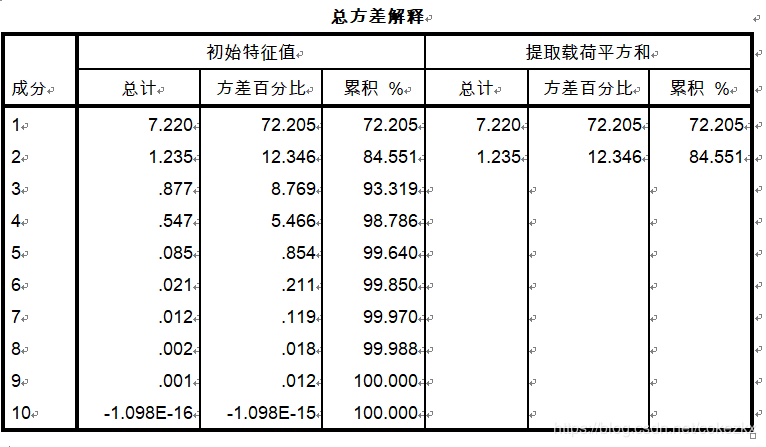
这两个表格的数须被用来计算最终总得分。
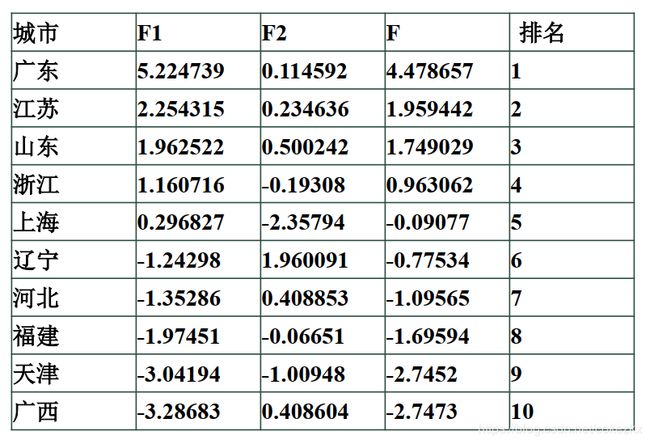
F1=0.353ZX1+0.042ZX2-0.041ZX3+0.364ZX4+0.367ZX5+0.366ZX6+0.352ZX7+0.364ZX8+0.298ZX9+0.355ZX10；
F2=0.175ZX1- 0.741ZX2+0.609ZX3- 0.004ZX4+0.063ZX5- 0.061ZX6-0.022ZX7+0.158ZX8-0.046ZX9-0.115ZX10
F=(72.2/84.5) F1 +(12.3/84.5) F2
ZXi是归一化后的自变量取值，归一化SPSS也可以作。
F1，F2的系数分别是成分矩阵中的数据除以主成分相对应的特征值开平方根，F的系数是方差百分比的比例。结果：

2.聚类分析

聚类分析是一种探索性的分析，在分类的过程中，人们不必事先给出一个分类的标准，聚类分析能够从样本数据出发，自动进行分类。聚类分析所使用方法的不同，常常会得到不同的结论。不同研究者对于同一组数据进行聚类分析，所得到的聚类数未必一致。因此我们说聚类分析是一种探索性的分析方法。用SPSS：

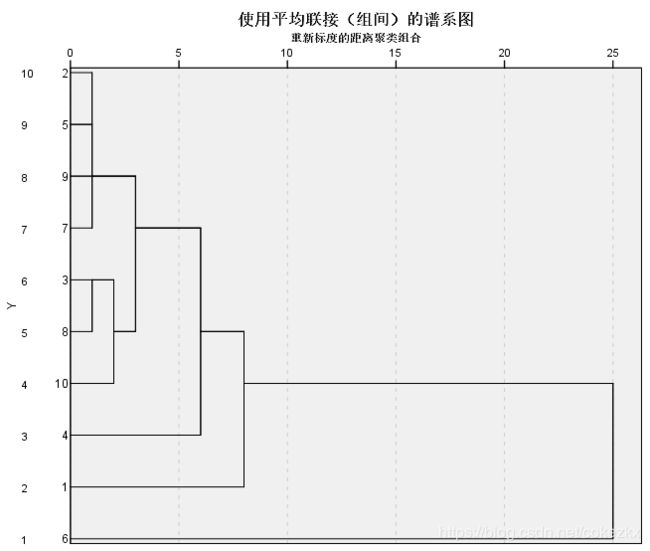
冰柱图：

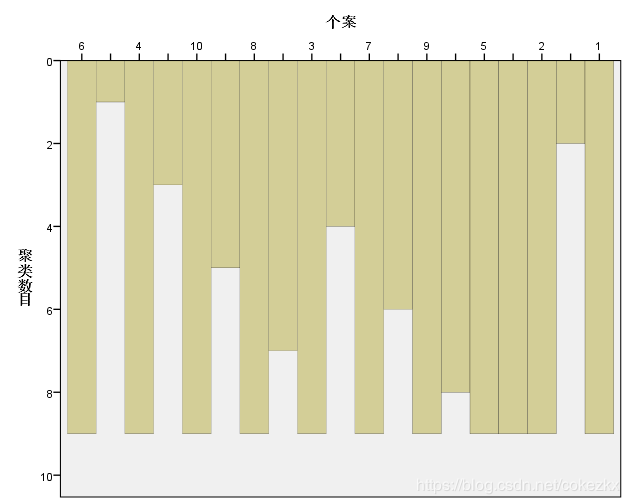
这个图的意义也是样本聚成类的顺序表示。

3.对策论

在日常生活中，经常看到一些具有相互之间斗争或竞争性质的行为。具有竞争或对
抗性质的行为称为对策行为。对策问题的特征是参与者为利益相互冲突的各方， 其结局不取决于其中任意一方的努力而是各方所采取的策略的综合结果。
例：在一场敌对的军事行动中，甲方拥有三种进攻性武器 A1, A2, A3 ，可分别用
于摧毁乙方工事；而乙方有三种防御性武器 B1, B2,B3 来对付甲方。据平时演习得到的数据，各种武器间对抗时，相互取胜的可能如下：
A1 对 B1 2： 1； A1 对 B2 3： 1； A1 对 B3 1： 2；
A2 对 B1 3： 7； A2 对 B2 3： 2； A2 对 B3 1： 3；
A3 对 B1 3： 1； A3 对 B2 1： 4； A3 对 B3 2： 1
解：先分别列出甲、乙双方的赢得的可能性矩阵，将甲方矩阵减去乙方矩阵的对应
元素，得零和对策时甲方的赢得矩阵如下：
A=[1/ 2 3/ 5 1/ 3；2/5 1/5 1/ 2；1/ 3 1/ 2 1/ 3];
编写程序如下:

a=[1/3,1/2,-1/3;-2/5,1/5,-1/2;1/2,-3/5,1/3];
b=10;
a=a+b*ones(3); %把赢得矩阵的每个元素变成大于0的数
[x0,u]=linprog(ones(3,1),-a',-ones(3,1),[],[],zeros(3,1));
x=x0/u,u=1/u-b
[y0,v]=linprog(-ones(3,1),a,ones(3,1),[],[],zeros(3,1));
y=y0/(-v),v=1/(-v)-b
Optimal solution found.


x =

    0.5283
         0
    0.4717


u =

   -0.0189


Optimal solution found.


y =

         0
    0.3774
    0.6226


v =

   -0.0189

u<0,故乙方有利。
lingo：

 model:
sets:
player1/1..3/:x;
player2/1..3/:y;
game(player1,player2):c;
endsets
data:
ctrl=?; !ctrl取1求局中人1的策略，ctrl取0求局中人2的策略;
c=0.3333333 0.5 -0.3333333
-0.4 0.2 -0.5
0.5 -0.6 0.3333333;
enddata
max=u*ctrl-v*(1-ctrl);
@free(u);@free(v);
@for(player2(j):@sum(player1(i):c(i,j)*x(i))>u);
 @for(player1(i):@sum(player2(j):c(i,j)*y(j))

实在看不懂，有机会的话改可能性矩阵c吧。
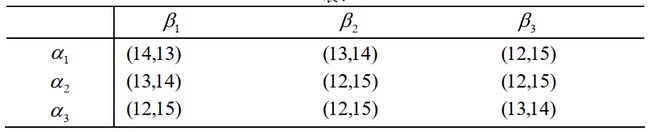
例2：有甲、乙两支游泳队举行包括三个项目的对抗赛。这两支游泳队各有一名健将级运动员（甲队为李，乙队为王），在三个项目中成绩都很突出，但规则准许他们每人只能参加两项比赛，每队的其他两名运动员可参加全部三项比赛。已知各运动员平时成绩（秒）见下表：

假定各运动员在比赛中都发挥正常水平，又比赛第一名得5分，第二名得3分，第
三名得1分，问教练员应决定让自己队健将参加哪两项比赛，使本队得分最多？（各队参加比赛名单互相保密，定下来后不准变动）
解：分别用α1 、 α 2 和α3 表示甲队中李姓健将不参加蝶泳、仰泳、蛙泳比赛的策
略，分别用 β1 、 β2 和 β3 表示乙队中王姓健将不参加蝶泳、仰泳、蛙泳比赛的策略。当甲队采用策略α1 ，乙队采用策略 β1 时，在100米蝶泳中，甲队中赵获第一、钱获第三得6分，乙队中张获第二，得3分；在100米仰泳中，甲队中李获第二，得3分，乙队中王获第一、张获第三，得6分；在100米蛙泳中，甲队中李获第一，得5分，乙队中王获第二、张获第三，得4分。也就是说，对应于策略 (α1, β1) ，甲、乙两队各自的得分为(14,13) 。代码：

a=[59.7 63.2 57.1 58.6 61.4 64.8
67.2 68.4 63.2 61.5 64.7 66.5
74.1 75.5 70.3 72.6 73.4 76.9];
m=3;n=3;kk=3;T=1000;
sc1=[5:-2:1,zeros(1,3)]; %1-6 名的得分
sc2=repmat(sc1,kk,1);
for i=1:m
	for j=1:n
		b=a;
		b(i,3)=T;b(j,4)=T; %不参加比赛，时间成绩取为充分大
		[b,ind]=sort(b,2); %对 b 的每一行进行排序
		for k=1:m
			sc2(k,ind(k,:))=sc1; %计算得分
		end
		A_sc(i,j)=sum(sum(sc2(:,1:m))); %统计得分
		B_sc(i,j)=sum(sum(sc2(:,m+1:end)));
	end
end
A_sc,B_sc
fid=fopen('txt2.txt','w');
fprintf(fid,'%f\n',A_sc');
fwrite(fid,'~','char'); %往纯文本文件中写 LINGO 数据的分割符
fprintf(fid,'%f\n',B_sc');
fclose(fid);

结果：

4.马氏链

一个随机试验的结果有多种可能性，在数学上用一个随机变量（或随机向量）来描述。在许多情况下，人们不仅需要对随机现象进行一次观测，而且要进行多次，甚至接连不断地观测它的变化过程。这就要研究无限多个，即一族随机变量。随机过程理论就是研究随机现象变化过程的概率规律性的。
设{ξt,t ∈T}是一族随机变量， T 是一个实数集合， 若对任意实数t ∈T,ξ(t)
是一个随机变量，则称{ξ(t) ,t ∈T}为随机过程。
T 称为参数集合，参数t 可以看作时间。 ξ(t) 的每一个可能取值称为随机过程的一个状态。其全体可能取值所构成的集合称为状态空间，记作E。当参数集合T 为非负整数集时，随机过程又称随机序列。本章要介绍的马尔可夫链就是一类特殊的随机序列。
一段粘贴来的白话：马尔可夫过程就是几个状态按一个转移概率矩阵做转移。这个转移概率就是问题中心，我们可以直接用输入序列统计出一个转移概率。如果是一个往复运动，例如钟摆，左边状态是0，中间是1，右边是2，那么序列就是01210121012101201210121···马尔可夫假设有一条是下一状态只取决于当前状态，如果当前状态是1，接下来是0或2的概率各占一半。
例：若顾客的购买是无记忆的，即已知现在顾客购买情况，未来顾客的购买情况
不受过去购买历史的影响，而只与现在购买情况有关。现在市场上供应 A、 B、 C 三个不同厂家生产的 50 克袋装味精，用“ξn =1”、 “ ξn = 2 ”、“ ξn = 3”分别表示“顾客第 n 次购买 A、 B、 C 厂的味精”。显然， {ξn ,n = 1,2…} 是一个马氏链。若已知第一次顾客购买三个厂味精的概率依次为 0.2， 0.4， 0.4。又知道一般顾客购买的倾向由下表给出，预测经过长期的多次购买之后，顾客的购买倾向如何？

解：方程组：

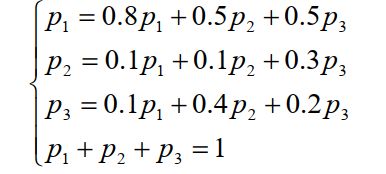
代码：

format rat
p=[0.8 0.1 0.1;0.5 0.1 0.4;0.5 0.3 0.2];
a=[p'-eye(3);ones(1,3)];
b=[zeros(3,1);1];
p_limit=a\b

p_limit =

       5/7     
      11/84    
      13/84   

这个题感觉没啥难度，看到应用性更强的再粘。