动态规划（一）硬币找零，机器人路径

动态规划（Dynamic Programming，简称DP），虽然抽象后进行求解的思路并不复杂，但具体的形式千差万别，找出问题的子结构以及通过子结构重新构造最优解的过程很难统一，并不像回溯法具有解决绝大多数问题的银弹。

动态规划求解的一般思路

1.硬币找零

　　扩展1：单路取苹果

　　扩展2：机器人路径

2.字符串相似度/编辑距离（edit distance）

　　应用1：子串匹配

　　应用2：最长公共子序列

3.最长公共子序列(Longest Common Subsequence,lcs)

　　扩展1：输出所有lcs

　　扩展2：通过LCS获得最长递增自子序列

4.最长递增子序列（Longest Increasing Subsequence,lis）

　　扩展：求解lis的加速

5.最大连续子序列和/积

　　扩展1：正浮点数数组求最大连续子序列积

　　扩展2：任意浮点数数组求最大连续子序列积

6.矩阵链乘法

　　扩展：矩阵链乘法的备忘录解法（伪码）

7.0-1背包问题

8.有代价的最短路径

9.瓷砖覆盖（状态压缩DP）

10.工作量划分

11.三路取苹果

参考资料

附录1：其他的一些动态规划问题与解答（链接）

附录2：《算法设计手册》第八章 动态规划 面试题解答

动态规划求解的一般思路：

　　判断问题的子结构（也可看作状态），当具有最优子结构时，动态规划可能适用。

　　求解重叠子问题。一个递归算法不断地调用同一问题，递归可以转化为查表从而利用子问题的解。分治法则不同，每次递归都产生新的问题。

　　重新构造一个最优解。

备忘录法：

　　动态规划的一种变形，使用自顶向下的策略，更像递归算法。

　　初始化时表中填入一个特殊值表示待填入，当递归算法第一次遇到一个子问题时，计算并填表；以后每次遇到时只需返回以前填入的值。

　　实例可以参照矩阵链乘法部分。

1.硬币表示

有数量不限的硬币，币值为25分、10分、5分和1分，请编写代码计算n分有几种表示法。
给定一个int n，请返回n分有几种表示法。保证n小于等于100000，为了防止溢出，请将答案Mod 1000000007。
测试样例：
6
返回：2

//二维dp
public int countWays(int n) {
    int A[] = {1, 5, 10, 25}, dp[][] = new int[A.length][n + 1];
    for (int j = 0; j <= n; j++) {
        dp[0][j] = 1;
    }
    for (int i = 1; i < A.length; i++) {
        for (int j = 0; j <= n; j++) {
            int t = j - A[i];
            if (t >= 0) {
                dp[i][j] = (dp[i - 1][j] + dp[i][t]) % 1000000007;
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }

    return dp[A.length - 1][n];
}

//一维dp
public int countWays(int n) {
    int dp[] = new int[n + 1], i, A[] = {1, 5, 10, 25};
    for (i = 0, dp[0] = 1; i < A.length; i++) {
        for (int j = A[i]; j <= n; j++) {
            dp[j] = (dp[j] + dp[j - A[i]]) % 1000000007;
        }
    }

    return dp[n];
}

class Coins {
public:
    int countWays(int n) {
        // write code here
        int coins[4]={1,5,10,25};
        int dp[100001] = {0};       
        dp[0] = 1;
        for(int i = 0;i < 4;++i){
            for(int j = coins[i];j <= n;++j){
                dp[j] =(dp[j]+dp[j-coins[i]])%1000000007;               
            }
        }
        return dp[n];
    }
};

硬币表示_牛客网
https://www.nowcoder.com/questionTerminal/c0503ca0a12d4256af33fce2712d7b24

1.1取苹果

动态规划之收集苹果 - lol霖 - 博客园
https://www.cnblogs.com/lihonglin2016/p/4298432.html
路径经过的最大值（最小值）：
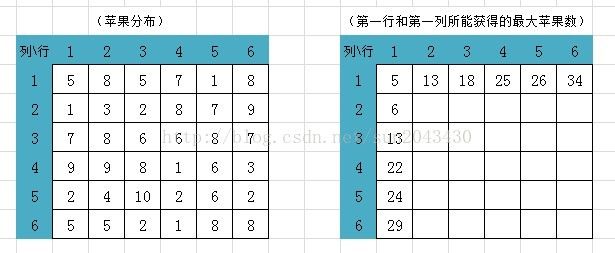
原题：平面上有N*M个格子，每个格子中放着一定数量的苹果。从左上角的格子开始， 每一步只能向下走或是向右走，每次走到一个格子就把格子里的苹果收集起来， 这样一直走到右下角，问最多能收集到多少个苹果。

不妨用一个表格来表示：

{5, 8, 5, 7, 1, 8},
{1, 3, 2, 8, 7, 9},
{7, 8, 6, 6, 8, 7},
{9, 9, 8, 1, 6, 3},
{2, 4,10, 2, 6, 2},
{5, 5, 2, 1, 8, 8},

接下来填第2行，首先是第2行第2列的值，应该填写为 MAX（A[1，2], A[2，1]）+ A[2，2]对应的苹果数量。也就是说到达第2行第2列能获得的最大苹果数，要看第2行第1列所获得的苹果数（6）和第1行第2列所获得的苹果数（13），这两者哪个更大，谁大就取谁的值，显然第1行第2列所获得的苹果数（13）更大，所以用13加上第2行第2列的苹果数3 = 16，就是到达第2行第2列能获得的最大苹果数。同理，填所在格能获得的最大苹果数就是看它左面一格和上面一格哪个值更大，就取哪个值再加上自己格子里面的苹果数，就是到达此格能获得的最大苹果数。依此填完所有格子，最后得到下图：

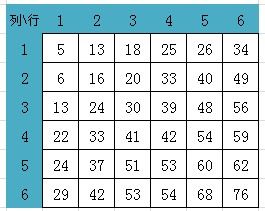
所以：到达右下角能够获得的最大苹果数量是76。所经过的路径可以通过倒推的方法得到，从右下角开始看所在格子的左边一格和上面一格哪边大就往哪边走，如果遇到一样大的，任选一条即可。

这样我们可以画出路线图，如下图右边表格：

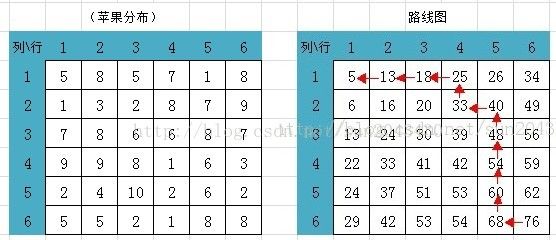
这个例子的分析和解决方法大概就是这样了。在前面第一个例子里面我们提到：空间换时间是动态规划的精髓。但是一个问题是否能够用动态规划算法来解决，需要看这个问题是否能被分解为更小的问题（子问题）。而子问题之间是否有包含的关系，是区别动态规划算法和分治法的所在。一般来说，分治法的各个子问题之间是相互独立的，比如折半查找（二分查找）、归并排序等。而动态规划算法的子问题在往下细分为更小的子问题时往往会遇到重复的子问题，我们只处理同一个子问题一次，将子问题的结果保存下来，这就是动态规划的最大特点。

首先，我们要找到这个问题中的“状态”是什么？我们必须注意到的一点是，到达一个格子的方式最多只有两种：从左边来的(除了第一列)和从上边来的(除了第一行)。因此为了求出到达当前格子后最多能收集到多少个苹果，我们就要先去考察那些能到达当前这个格子的格子，到达它们最多能收集到多少个苹果。 (是不是有点绕，但这句话的本质其实是DP的关键：欲求问题的解，先要去求子问题的解)

经过上面的分析，很容易可以得出问题的状态和状态转移方程。状态S[i][j]表示我们走到(i, j)这个格子时，最多能收集到多少个苹果。那么，状态转移方程如下：

S[i][j]=A[i][j] + max(S[i-1][j], if i>0 ; S[i][j-1], if j>0)
其中i代表行，j代表列，下标均从0开始；A[i][j]代表格子(i, j)处的苹果数量。

S[i][j]有两种计算方式：1.对于每一行，从左向右计算，然后从上到下逐行处理；2. 对于每一列，从上到下计算，然后从左向右逐列处理。这样做的目的是为了在计算S[i][j]时，S[i-1][j]和S[i][j-1]都已经计算出来了。

动态规划算法总结起来就是两点：

1 寻找递推（递归）关系，比较专业的说法叫做状态转移方程。

2 保存中间状态，空间换时间。

#include  
#include  
using namespace std;  
int a[100][100];  
int dp[100][100];  
int m,n;  

void dp_fun(int x,int y)  
{  
    dp[x][y] = a[x][y];  
    int max = 0;  
    if(x > 0 && max < dp[x-1][y])  
    {  
        max = dp[x-1][y];  
    }  
    if(y > 0 && max < dp[x][y-1])  
    {  
        max = dp[x][y-1];  
    }  
    dp[x][y] += max;  
    if(x1)  
    {  
        dp_fun(x+1,y);  
    }     
    if(y1)  
    {  
        dp_fun(x,y+1);  
    }  
    return;  
}   

int main()  
{  
    memset(dp,0,sizeof(dp));   
    cin>>m>>n;  
    for(int i=0;ifor(int j=0;jcin>>a[i][j];  
        }  
    }     
    dp_fun(0,0);  
    for(int i=0;ifor(int j=0;jcout<"\t";  
        }  
        cout<return 0;  
}  

1.2机器人走方格
题目描述
有一个XxY的网格，一个机器人只能走格点且只能向右或向下走，要从左上角走到右下角。请设计一个算法，计算机器人有多少种走法。
给定两个正整数int x,int y，请返回机器人的走法数目。保证x＋y小于等于12。
测试样例：
2,2
返回：2

/ 题目要求走的是大格子而不是网格线的交点，所以有两种走法。
// 二维数组用于计算走到当前格子的走法总数，为其上方格子走法总数与其左侧格子走法总数之和

class Robot {
public:
    int countWays(int x, int y) {
        // write code ,here
        int dp[13][13]={0};
        dp[0][0]=0;
        for(int i=1;i//第一行初始化，因为只有横着走一种方法。
             dp[0][i]=1;
         for(int i=1;i//第一列初始化，因为只有竖着一种方法。
            dp[i][0]=1;
         for(int i=1;i//dp[i][j]的方法，等于走到上面一格和走到左边一个方法之和。
              for(int j=1;j1][j]+dp[i][j-1];
              }
         return dp[x-1][y-1];      
    }
};

题目描述
有一个XxY的网格，一个机器人只能走格点且只能向右或向下走，要从左上角走到右下角。请设计一个算法，计算机器人有多少种走法。注意这次的网格中有些障碍点是不能走的。
给定一个int[][] map(C++ 中为vector >),表示网格图，若map[i][j]为1则说明该点不是障碍点，否则则为障碍。另外给定int x,int y，表示网格的大小。请返回机器人从(0,0)走到(x - 1,y - 1)的走法数，为了防止溢出，请将结果Mod 1000000007。保证x和y均小于等于50

class Robot {
public:
    int countWays(vector<vector<int> > map, int x, int y) {
         if(map.size() != x || map[0].size() != y)
        {
            return 0;
        }
        int dp[100][100]={0};
       dp[0][0] = 1;
         for(int i=0;i//dp[i][j]的方法，等于走到上面一格和走到左边一个方法之和。
              for(int j=0;jif(map[i][j] != 1) 
                  {
                      dp[i][j]=0;
                       continue;
                  }
                  if(i == 0 || j == 0)
                  {
                      if(i == 0 && j != 0)
                      {
                          dp[i][j] = dp[i][j-1];
                      }
                       if(i != 0 && j == 0)
                      {
                          dp[i][j] = dp[i-1][j];
                      }
                      continue;
                  }
                  dp[i][j]=(dp[i-1][j]+dp[i][j-1])%1000000007;

              }
         return dp[x-1][y-1];      

    }
};