2D空间中使用Quadtree四叉树进行碰撞检测优化

【原文】Quick Tip: Use Quadtrees to Detect Likely Collisions in 2D Space

---

很多游戏中都需要使用碰撞检测算法检测两个物体的碰撞，但通常这些碰撞检测算法都很耗时很容易拖慢游戏的速度。这里我们学习一下使用四叉树来对碰撞检测进行优化，优化的根本是碰撞检测时跳过那些明显离得很远的物体，加快检测速度。

【注：这里算法的实现使用的Java语言，但算法和语言没有关系，理解了其中的原理可以应用到各种碰撞检测场景中。】

介绍

碰撞检测是多数游戏的关键部分，不管是2d游戏还是3d游戏中，检测两个物体的碰撞都是很重要的，否则会出现很奇怪的现象。

width="600" height="450" src="https://www.youtube.com/embed/_viW2ZUMlvo" allowfullscreen="">

碰撞检测是一个很耗费资源的操作。假设有100个物体要进行互相的碰撞检测，两两物体的位置比较要进行：100x100 = 10000次，检测的次数实在太多。

碰撞检测优化的一个办法就是想办法减少检测的次数，例如在屏幕对角的两个物体那么远是不可能碰撞的所以也就没必要去判断他们是否碰撞了，四叉树的优化就是基于这一点。

关于四叉树

四叉树是二叉树的一个扩展也是一个数据结构，只不过四叉树是有四个子节点。四叉树将2d区域分成多个部分来进行划分操作。

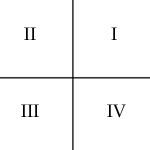
在接下来的示例图片中，每张图片代表一个游戏的2d空间，红色的方块代表物体。同时本文中每个区域的子区域（子节点）按照逆时针进行标记如下：

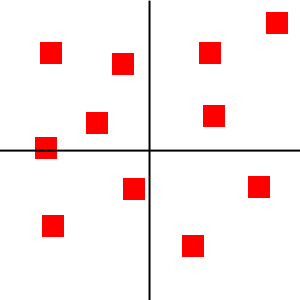
一个四叉树的开始是一个单一节点（根节点），根节点对应原本还没有分割的2d空间，物体可以添加到2d空间，也就是添加到根节点上。

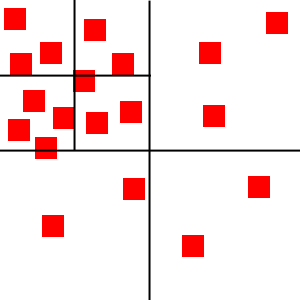
当更多的物体添加到四叉树以后，根节点物体数量太多了就会分裂出四个子节点，将多数物体分给子节点中（处于子节点边界的物体无法加入任何一个子节点就还是留给父节点）。

同样随着物体数量增加每一个子节点可以继续分裂出自己的四个子节点。

可以看到每个节点只包含少量的物体（不能分给子节点的那些物体）。因此我们知道，在左上节点中的物体是不可能和左下节点中的物体产生碰撞的，因此就不需要在他们之间进行碰撞检测。

四叉树的实现

四叉树的一个非常好的JavaScript实现例子：javascript-quadtree-implementation

四叉树的实现很简单，这里的实现代码使用的Java语言，但这个技术可以应用到任何语言当中。

【译者注】：这里的Java实现中坐标系原点位于左上角，物体的锚点也位于左上角。

首先是Quadtree的核心类：

Quadtree.java

public class Quadtree {

  private int MAX_OBJECTS = 10;
  private int MAX_LEVELS = 5;

  private int level;        // 子节点深度
  private List objects;     // 物体数组
  private Rectangle bounds; // 区域边界
  private Quadtree[] nodes; // 四个子节点

 /*
  * 构造函数
  */
  public Quadtree(int pLevel, Rectangle pBounds) {
   level = pLevel;
   objects = new ArrayList();
   bounds = pBounds;
   nodes = new Quadtree[4];
  }
}

Quadtree类的结构很清楚：

• MAX_OBJECTS：定义的是一个区域节点在被划分之前能够拥有节点的最大数量；
• MAX_LEVELS：定义的是子节点的最大深度；
• level：指的是当前节点的深度，对于自身来说level为0；
• bounds：指的是当前节点所占的2d空间；
• nodes：四个子节点。

在这个例子中，四叉树中要碰撞检测的物体都是些小矩形，实际可能会有任意形状的物体，这个和四叉树检测优化算法本身无关，只是不同行的物体检测要采用不同的检测方法（圆形检测、矩形检测等），一般也都会将不规则物体简化为规则形状。

然后要实现四叉树的五个方法：clear, split, getIndex, insert和 retrieve

clear方法递归清除所有节点所拥有的物体：

/*
 * 清空四叉树
 */
 public void clear() {
   objects.clear();

   for (int i = 0; i < nodes.length; i++) {
     if (nodes[i] != null) {
       nodes[i].clear();
       nodes[i] = null;
     }
   }
 }

split函数将当前节点平均分成四个子节点，并用计算好的新节点数据初始化四个子节点：

/*
 * 将一个节点分成四个子节点（实际是添加四个子节点）
 */
 private void split() {
   int subWidth = (int)(bounds.getWidth() / 2);
   int subHeight = (int)(bounds.getHeight() / 2);
   int x = (int)bounds.getX();
   int y = (int)bounds.getY();

   nodes[0] = new Quadtree(level+1, new Rectangle(x + subWidth, y, subWidth, subHeight));
   nodes[1] = new Quadtree(level+1, new Rectangle(x, y, subWidth, subHeight));
   nodes[2] = new Quadtree(level+1, new Rectangle(x, y + subHeight, subWidth, subHeight));
   nodes[3] = new Quadtree(level+1, new Rectangle(x + subWidth, y + subHeight, subWidth, subHeight));
 }

getIndex函数判断物体属于父节点还是子节点，以及属于哪一个子节点：

/*
 * 用于判断物体属于哪个子节点
 * -1指的是当前节点可能在子节点之间的边界上不属于四个子节点而还是属于父节点
 */

 private int getIndex(Rectangle pRect) {
   int index = -1;
   // 中线
   double verticalMidpoint = bounds.getX() + (bounds.getWidth() / 2);
   double horizontalMidpoint = bounds.getY() + (bounds.getHeight() / 2);

   // 物体完全位于上面两个节点所在区域
   boolean topQuadrant = (pRect.getY() < horizontalMidpoint && pRect.getY() + pRect.getHeight() < horizontalMidpoint);
   // 物体完全位于下面两个节点所在区域
   boolean bottomQuadrant = (pRect.getY() > horizontalMidpoint);

   // 物体完全位于左面两个节点所在区域
   if (pRect.getX() < verticalMidpoint && pRect.getX() + pRect.getWidth() < verticalMidpoint) {
      if (topQuadrant) {
        index = 1; // 处于左上节点 
      }
      else if (bottomQuadrant) {
        index = 2; // 处于左下节点
      }
    }
    // 物体完全位于右面两个节点所在区域
    else if (pRect.getX() > verticalMidpoint) {
     if (topQuadrant) {
       index = 0; // 处于右上节点
     }
     else if (bottomQuadrant) {
       index = 3; // 处于右下节点
     }
   }

   return index;
 }

insert函数往四叉树中添加物体，如果物体可以分给子节点则分给子节点，否则就留给父节点了，父节点物体超出容量后如果没分裂的话就分裂从而将物体分给子节点：

/*
 * 将物体插入四叉树
 * 如果当前节点的物体个数超出容量了就将该节点分裂成四个从而让多数节点分给子节点
 */
 public void insert(Rectangle pRect) {

    // 插入到子节点
   if (nodes[0] != null) {
     int index = getIndex(pRect);

     if (index != -1) {
       nodes[index].insert(pRect);

       return;
     }
   }

    // 还没分裂或者插入到子节点失败，只好留给父节点了
   objects.add(pRect);

    // 超容量后如果没有分裂则分裂
   if (objects.size() > MAX_OBJECTS && level < MAX_LEVELS) {
      if (nodes[0] == null) { 
         split(); 
      }
      // 分裂后要将父节点的物体分给子节点们
     int i = 0;
     while (i < objects.size()) {
       int index = getIndex(objects.get(i));
       if (index != -1) {
         nodes[index].insert(objects.remove(i));
       }
       else {
         i++;
       }
     }
   }
 }

最后一个是retrieve函数，这个函数返回所有可能和指定物体碰撞的物体，也就是待检测物体的筛选，这也是优化碰撞检测的关键：

/*
 * 返回所有可能和指定物体碰撞的物体
 */
 public List retrieve(List returnObjects, Rectangle pRect) {
   int index = getIndex(pRect);
   if (index != -1 && nodes[0] != null) {
     nodes[index].retrieve(returnObjects, pRect);
   }

   returnObjects.addAll(objects);

   return returnObjects;
 }

应用于2d碰撞检测

实现了四叉树数据结构之后我们就可以用来优化碰撞检测减少检测次数了。

典型的，游戏开始要创建四叉树并指定游戏场景的边界尺寸：

Quadtree quad = new Quadtree(0, new Rectangle(0,0,600,600));

在每一帧都要使用clear函数清空四叉树然后使用insert函数将所有物体重新添加到四叉树中：

quad.clear();
for (int i = 0; i < allObjects.size(); i++) {
  quad.insert(allObjects.get(i));
}

所有物体都插入以后，要遍历所有的物体并使用retrieve函数筛选出所有可能碰撞的物体进行碰撞检测。

List returnObjects = new ArrayList();
for (int i = 0; i < allObjects.size(); i++) {
  returnObjects.clear();
  quad.retrieve(returnObjects, objects.get(i));

  for (int x = 0; x < returnObjects.size(); x++) {
    // 使用合适的碰撞检测算法和每一个可能碰撞的物体进行碰撞检测...
  }
}

关于碰撞检测算法文章（之后也会再翻译）：碰撞检测

结论

总之碰撞检测是一个很耗费资源的操作，通过四叉树结构减少检测的次数可以大大优化碰撞检测效率，帮助减轻碰撞检测对游戏的拖延。