数据结构基础18:二叉搜索树的搜索、插入、删除和升序输出
前言: HashMap 的底层实现中用到了红黑树,红黑树其实是二叉搜索平衡树,我们先了解一下二叉搜索树。
哈希表的字典操作(查找、插入和删除)的平均时间复杂度为Θ(1),而这些操作在坏的情况下能的时间与字典的元素个数呈线性关系。当HashMap的链表长度超过8时,就需要用到平衡二叉搜索树红黑树,红黑树的字典操作时间复杂度为o(logN),能保证哈希冲突过多时的性能;而且二叉搜索树中的节点是有顺序的,可以在Θ(n)时间内按升序输出字典的元素,这是哈希表没有的优势。
一、二叉搜索树的定义
1、二叉搜索树(Binary Search Tree),又被称为二叉查找/排序树,是一颗特殊的二叉树。
时间复杂度:二叉搜索树的查找、插入和删除的平均时间为Θ(logN),最坏的时间为Θ(n)
二叉搜索树需满足以下四个条件:
- 每个元素有一个关键字,并且任意两个元素的关键字都不同
- 若任意节点的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若任意节点的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 任意节点的左、右子树也分别为二叉查找树;
索引二叉搜索树:源于普通的二叉搜索,只是在每个节点中添加一个leftSize域。这个域的值是该节点左子树的元素个数。leftSize同时给出了一个元素的索引,即该元素的左子树排在该元素之前。
2、借鉴二分查找的高效率,对普通二叉树按一定顺序组织成二叉搜索树可以大大提升数据的查找效率。通常情况下查找效率在O(logN)。但二叉搜索树对数的结构没有限制,所有在最坏情况下会出现O(N),为了保证查找效率,我们需要对二叉树的结构进行限制,接着出现了平衡二叉搜索树。
3、平衡二叉搜索树
平衡二叉搜索树控制它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。这样就保证了查找效率维持在O(lgN),如果进行加入或是删除操作,对数据的结构造成破坏,需要对树形及时调整。
4、红黑树
红黑树是平衡二叉搜索树的一种实现,但是对树的高度差控制没有那么严格,只是要求一个子树的高度不能高于另一个子树高度的二倍,所以查找效率没有多大的影响,但是红黑树相比于平衡二叉树的一大优势就是所有的数结构的调整都可以在3次旋转之内完成,效率上得到了很大的提升。
一颗红黑树需满足:
(1)每个节点或者是黑色,或者是红色。
(2)根节点是黑色。
(3)每个叶子节点(NIL)是黑色。 [注意:这里叶子节点,是指为空(NIL或NULL)的哨兵节点。]
(4)如果一个节点是红色的,则它的子节点必须是黑色的。
(5)从一个节点到该节点的子孙节点的所有路径上包含相同数目的黑节点。
二、二叉搜索树常用操作
通常采取二叉链表作为二叉搜索树的存储结构。
1、二叉搜索树节点定义:为二叉树的每个元素添加一个关键字T key即可,与原来的数据value形成数对。
/*
* 二叉搜索树定义
*/
public class BSTree
{
//属性成员
public BSTNode root; // 根结点
//二叉搜索节点内部类
class BSTNode
{
int key; // 关键字
T value; //存储的数据值
BSTNode left; // 左孩子
BSTNode right; // 右孩子
public BSTNode(T key,T value)
{
this.key = key;
this.value = value;
this.left = left;
this.right = right;
}
}
//方法成员
/*
search(T key):返回关键字为k的数对
insert(p):插入数对pair
erase(T key):删除关键字为k的数对
ascend():按关键字升序输出所有数对
*/
} 2、搜索节点
搜索关键字为key的节点并返回。该过程的时间复杂度为O(h),其中h是树的高度。
由于二叉搜索树定义上的特殊性,只需根据输入的 key 值从根开始进行比较,若小于根的 key 值,则与根的左子树比较,大于根的key值与根的右子树比较,以此类推,找到则返回相应节点,否则返回 null。
/*
* 1、返回关键字为k的数对
*/
public BSTNode search(int key)
{
BSTNode currentNode = root;
while (currentNode != null)
{
if(keycurrentNode.key)
currentNode = currentNode.rightChild;
else
return currentNode;//找到匹配的元素
}
}
return null;//无匹配的数对
} 3、插入节点
把数对(key,value)插入二叉树中。要插入一个元素,首先要通过查找来确定。
与查找操作相似,由于二叉搜索树的特殊性,待插入的节点也需要从根节点开始进行比较,小于根节点则与根节点左子树比较,反之则与右子树比较,迭代此过程直到左子树为空或右子树为空,则插入到相应为空的位置。如果在比较的过程中置如果搜索到相同关键字的节点,就用pair.value覆盖掉该节点的值。
要注意保存父节点的信息 ,待插入的位置是父节点的左子树还是右子树,才能插入到正确的位。
/*
*2、 插入节点:要插入一个元素,首先要通过查找来确定
*/
public void insert(int key, int value)
{
if(root == null)
{
root = new BSTNode(key, value);
return;
}
BSTNode currentNode = root;
BSTNode parentNode = root;
boolean isLeftChild = true;
while (currentNode != null)
{
parentNode = currentNode;
if (key < currentNode.key)
{
currentNode = currentNode.leftChild;
isLeftChild = true;
} else {
currentNode = currentNode.rightChild;
isLeftChild = false;
}
}
BSTNode newNode = new BSTNode(key, value);
if (isLeftChild)
{
parentNode.leftChild = newNode;
}
else
{
parentNode.rightChild = newNode;
}
} 4、删除
在二叉搜索树的代码实现中,最难的是删除,因为这涉及到三种情况::
待删除节点是叶节点(没有子树):最简单,直接删除,将该节点置为null即可
待删除节点有一个子节点(左子树或右子树):是该节点的父节点指向该节点的子节点.见图1
待删除节点既有左孩子又有右孩子:用其右子树中的最小值(或左子树的最大元素)代替该节点上的值,删除其右子树上的最小值.见图2.
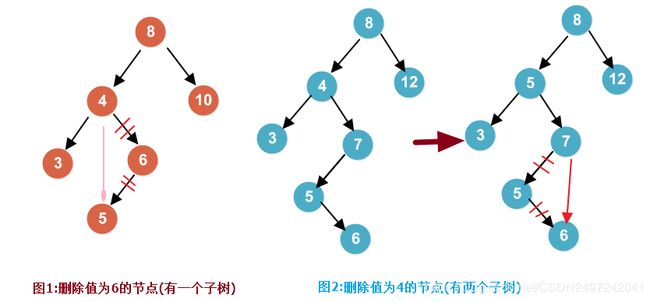 图1
图1
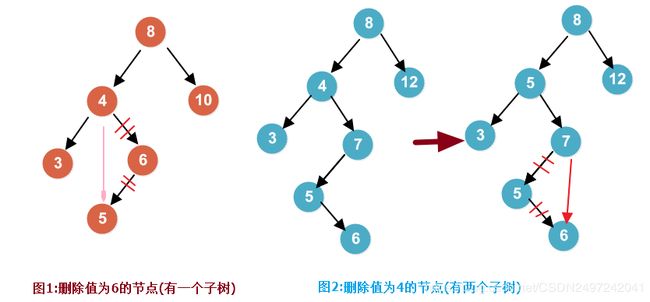 图2
图2
/**
* 删除指定key的节点
*/
public void deleteNode(int key)
{
//如果二叉搜索树中没有对应key的节点,那么不执行删除操作
if(search(key)==null)
return;
//否则肯定有key节点,首先定位到这个节点
BSTNode currentNode = root;
BSTNode currentNodeParentNode= null; //当前节点的父亲节点
while( currentNode.key!=key)
{
//如果要删除的节点key比当前节点的key小,那么说明要删除的节点在左子树中
if(key maxNode = currentNode.leftChild; //这变量存放了要找的最大节点
BSTNode maxNodeParentNode= currentNode; //这变量存放了要找的最大节点的父节点
while(maxNode.rightChild!=null){
//向右移动
maxNodeParentNode=maxNode;
maxNode= maxNode.rightChild;
}
//把最大节点插入到currentNode中,从而维持了原有的结构不变
currentNode.key = maxNode.key;
currentNode.value = maxNode.value;
//删除左子树的原最大节点
maxNodeParentNode.rightChild= null;
return ;
}
//情况2,如果当前节点既没有左节点又没有右节点,则直接丢弃
if(( currentNode.rightChild==null) && (currentNode.rightChild==null) )
{
//如果当前节点为根节点,那么删除根节点
if(currentNode==root){
root=null;
}
//如果当前节点不为根节点,那么必定有父亲节点,这时候只要丢弃当前节点就可以了,判断是判断当前节点是父亲节点的左儿子还是右儿子
if(currentNode==currentNodeParentNode.leftChild){
currentNodeParentNode.leftChild=null;
}
else
currentNodeParentNode.rightChild = null;
return;
}
//情况3,如果当前节点只有左节点或者右节点中的1个,那么把儿子提升上来
else
{
//如果只有左节点
if( currentNode.leftChild!=null){
//如果当前节点为根节点,那么吧左节点提升上来当根节点
if(currentNode==root){
root=currentNode.leftChild;
}
//如果当前节点不为根节点,那么必定有父节点,则判断当前节点是父亲节点的左儿子还是右儿子,并且用左节点值取代之
else if(currentNode==currentNodeParentNode.leftChild){
currentNodeParentNode.leftChild= currentNode.leftChild;
}
else
currentNodeParentNode.rightChild=currentNode.leftChild;
}
//如果只有右节点
else{
//如果当前节点为根节点,那么吧右节点提升上来当根节点
if(currentNode==root){
root=currentNode.rightChild;
}
//如果当前节点不为根节点,那么必定有父节点,则判断当前节点是父亲节点的左儿子还是右儿子,并且用右节点值取代之
if(currentNode==currentNodeParentNode.leftChild){
currentNodeParentNode.leftChild = currentNode.rightChild;
}
else
currentNodeParentNode.rightChild = currentNode.rightChild;
}
}
}
5、升序输出二叉查找树:
由于二叉搜索的特性,一个节点的左子节点的值都比它的值小,右子节点的值都比它的值大
因此采用中序遍历的方法(左,根,右)按升序输出所有节点值。
/**
* 4、升序输出所有节点:因为二叉搜索树中,左<根<右,所以我们可以用中序遍历的方法来升序打印出所有的节点
*/
public void ascendPrintAllNodes()
{
midOrder(root);
}
/**
* 中序遍历某节点,它会先打印左边节点,再打印当前节点,最后打印出右边节点
*/
private void midOrder(BSTNode currentNode)
{
//当前节点如果是null,则不打印出当前节点,并且退出递归
if(currentNode!=null)
{
midOrder(currentNode.leftChild);
System.out.print(currentNode.value+" ");
midOrder(currentNode.rightChild);
}
} 6、返回含有最大或最小值的节点
根据root一直遍历它的左孩子或右孩子。
/*
* 5、返回最大/小节点:
*/
private BSTNode maxNode(BSTNode root) {
if (root == null)
return null;
while(root.rightChild != null)
root = root.rightChild;
return root;
} 三、二叉搜索树的应用
用来实现平衡二叉搜索树红黑树
