周一到周五,每天一篇,北京时间早上7点准时更新~
OpenGL represents a 4 × 4 matrix not as a two-dimensional array of floating values, but rather as a single array of 16 floating-point values(OpenGL中用16个浮点数来表示矩阵,而不是用二维浮点数数组). By default, OpenGL uses a columnmajor or column-primary layout for matrices(默认情况下,OpenGL使用的是列序的矩阵). That is, for a 4 × 4 matrix, the first four elements represent the first column of the matrix, the next four elements represent the second column, and so on(意思就是说,对于4x4个元素的矩阵来说,前四个浮点数表示的是矩阵的第一列,接着的第二个四个浮点数是矩阵第二列,以此类推). This approach is different from many math libraries, which do take the two-dimensional array approach(很多数学库跟这个不一样,他们使用二维数组的方式去实现). For example, OpenGL prefers the first of these two examples:(比如OpenGL选择使用下面例子中的前者:)
GLfloat matrix[16]; // Nice OpenGL-friendly matrix
GLfloat matrix[4][4]; // Not as convenient for OpenGL programmersOpenGL can use the second variation, but the first is a more efficient representation(OpenGL可以使用第二种,但是第一种表达方式更高效). The reason for this will become clear in a moment(为何如此,一会就清楚了). These 16 elements represent the 4 × 4 matrix, as shown below(16个元素达标的4x4矩阵如下所示). When the array elements traverse down the matrix columns one by one, we call this column-major matrix ordering(当我们遍历数组元素的时候,我们管这叫列序矩阵). In memory, the 4 × 4 approach of the two-dimensional array (the second option in the preceding code) is laid out in a row-major order(在内存里,二维数组是以行序存储的). In math terms, the two orientations are the transpose of each other(数学里,这两种方式互为转置)
Representing the above matrix in colum-major order in memory produces an array as follows:(列序矩阵如下所示)
static const float A[] =
{
A00, A01, A02, A03, A10, A11, A12, A13,
A20, A21, A22, A23, A30, A31, A32, A33
};In contrast, representing it in row-major order would require a layout such as this:(而行序矩阵的表达则如下:)
static const float A[] =
{
A00, A10, A20, A30, A01, A11, A21, A31,
A20, A21, A22, A23, A30, A31, A32, A33,
};The real magic lies in the fact that these 16 values can represent a particular position in space and an orientation of the three axes with respect to the viewer(这里神奇的地方就是,矩阵的这16个数字可以表达一个空间中的相对于观察者来说的特定位置以及在这个位置的朝向). Interpreting these numbers is not hard at all(解释这些数字并不难). The four columns each represent a four-element vector(四列元素分别是四个向量). To keep things simple for this book, we focus our attention on just the first three elements of the vectors in the first three columns(为了使的内容更简单,我们主要集中精力在前三个向量的前三个元素上). The fourth column vector contains the x, y, and z values of the transformed coordinate system’s origin(第四列元素的xyz表示的是位移).
The first three elements of the first three columns are just directional vectors that represent the orientation (vectors here are used to represent a direction) of the x, y, and z axes in space(前三列的前三个元素表达的是旋转). For most purposes, these three vectors are always at 90° angles from each other and are usually each of unit length (unless you are also applying a scale or shear)(大多数情况下,这三个向量都是两两垂直的,并且是一个单位向量). The mathematical term for this (in case you want to impress your friends) is orthonormal when the vectors are unit length, and orthogonal when they are not(数学意义上,如果这仨不是单位向量则是正交,如果是则是标准正交). Figure 4.5 shows the 4 × 4 transformation matrix with its components highlighted(图4.5标注出了4x4矩阵的这些元素). Notice that the last row of the matrix is all 0s with the exception of the very last element, which is 1.(注意到所有列向量的最后一个元素都是0,最后一个列向量的最后一个元素是1)
The upper-left 3 × 3 sub-matrix of the matrix shown in Figure 4.5 represents a rotation or orientation(左上的3x3矩阵表达了旋转). The last column of the matrix represents a translation or position.(最后一列向量表达的是位置)The most amazing thing is that if you have a 4 × 4 matrix that contains the position and orientation of a coordinate system, and you multiply a vertex expressed in the identity coordinate system (written as a column matrix or vector) by this matrix, the result is a new vertex that has been transformed to the new coordinate system(最神奇的事情就是,你使用4x4矩阵去乘以一个点的坐标之后,这个点会被转换到另一个坐标系里去). As a result, any position in space and any desired orientation can be uniquely defined by a 4 × 4 matrix, and if you multiply all of an object’s vertices by this matrix, you transform the entire object to the given location and orientation in space!(所以,任何一个空间中的位置以及朝向,都可以用唯一的用一个4x4矩阵表达出来,如果用这个矩阵乘以一个物体的所有点, 那么这个物体的所有点都会被转换到那个位置上的姿势上去)
In addition, if you transform an object’s vertices from one space to another using one matrix, you can then transform those vertices by yet another matrix, transforming them again into another coordinate space(补充一下,你可以把一个物体从一个坐标系转换到另一个坐标系,同时还可以继续把这些点再转换到下一个坐标系). Given matrices A and B and vector v, we know that(给出A、B俩矩阵和向量v,我们知道:)![]()
is equivalent to(等价于)![]()
This relationship arises because matrix multiplication is associative(因为矩阵乘法可以累加,所以他们有这样的关系). Here in lies the magic: It is possible to stack a whole bunch of transforms together by multiplying the matrices that represent those transforms and using the resulting matrix as a single term in the final product(也就是说:你可以把所有变换矩阵事先全部乘上,然后拿到结果矩阵再去对你的物体进行相关操作)
The final appearance of your scene or object can depend greatly on the order in which the modeling transformations are applied(你渲染物体的最终结果取决于这些变换矩阵的相乘的顺序). This is particularly true of translation and rotation. We can see this as a consequence of the associativity and commutativity rules for matrix multiplication(这是由于矩阵的性质决定滴). We can group together sequences of transformations in any way we like because matrix multiplication is associative, but the order in which the matrices appear in the multiplication matters because matrix multiplication is not commutative(我们可以用任意的方式去让一堆矩阵相乘,但不同顺序会得到不同的结果)
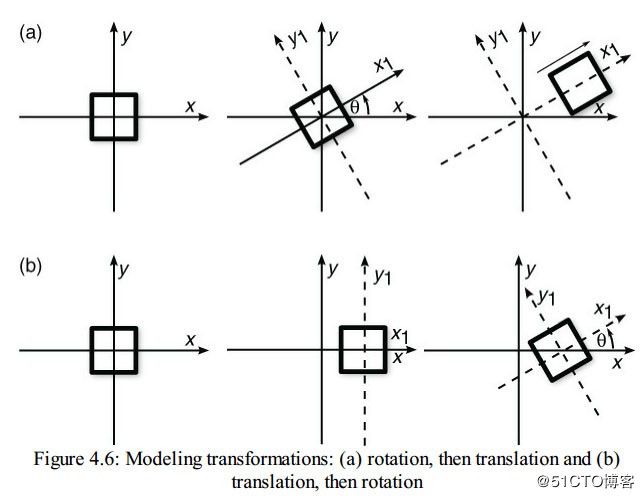
Figure 4.6(a) illustrates a progression of a square rotated first about the z axis and then translated down the newly transformed x axis, and Figure 4.6(b) illustrates first translating the same square along the x axis and then rotating it around around the z axis(图4.6a展示了先旋转后移动的效果,图4.6b展示了先移动后旋转的效果). The difference in the final dispositions of the square occurs because each transformation is performed with respect to the last transformation performed(这种差异产生的原因是因为,每一次变换是相对于上一次变换的结果来进行的). In Figure 4.6(a), the square is rotated with respect to the origin first(图4.6a中,旋转是相对于原点来做的). In Figure 4.6(b), after the square is translated, the rotation is performed around the newly translated origin(图4.6b中,旋转是相对于移动后的位置来做的)
第一时间获取最新桥段,请关注东汉书院以及图形之心公众号
东汉书院,等你来玩哦