多标签学习Ml-KNN算法

Ml-KNN: A Lazy Learning Approach to Multi-Label Learning

Pattern Recognition 40 (2007) 2038 – 2048

张敏灵，周志华

1 MLKNN简介

多标签学习来源于文本分类问题，一个文档可能同时属于几个不同的类别。在多标签学习中，训练集中的每个样例有多个标签，我们的主要任务是预测测试样本的标签集合。

多标签数据学习方法主要分为两种，一种问题转换法，包括转换为二分类、转换为标签排序、转换为多分类。另一种是算法适应法，包括Lazy learning(如ML-KNN)、Decision tree(如ML-DT)、Kernel learning(如Rank-svm)、Neural network(如BP-MLL)、information-theoretic(如CML)、Spectral analysis(如MLLS)。

MLKNN是由传统的K近邻（K-nearest neighbor，KNN）发展而来的，对于每一个测试样本，在训练集中找到它的K近邻。然后，基于邻居样本的统计信息，如属于相同类别的邻居的个数，用最大后验概率原则（MAP）决定测试样本的标签集合。

2 评价指标

多标签学习系统的评价指标与传统的单个标签学习系统不同，单标签任务常见的评价指标有accuracy、precision、 recall 、F-measure。多标签任务的评价指标更为复杂，主要有海明损失（Hamming loss，HL）、1-错误率（One-error，OE）、覆盖率（Coverage）、排序损失（Ranking loss，RL）、平均精度（Average precision，AVP）。

2.1 海明损失（Hamming loss，HL）

海明损失可以用来评估一个样本被错分多少次,例如，一个样本不属于标签A但是被错分成标签A，或者是，一个样本属于标签A，但是没有被预测为标签A。

也可以说，用海明损失来计算分类器预测出的结果序列与结果序列之间的数值上的距离。海明损失越小，预测结果越好。
$$HL=\frac{1}{m}.\sum _{i=1}^m\frac{|Y_i\Delta Z_i|}{M}$$
$m$–样本个数
$M$–所有标签总个数
$Y_i$–样本i实际标签的集合
$Z_i$–样本i预测标签的集合
$\Delta$–两个集合的对称差，异或

2.2 1-错误率（One-error，OE）

1-错误率可以用来评估在输出结果中排序第一的标签并不属于实际标签集中的概率。相当于单标签分类问题中的评价指标error。1-错误率越小，预测结果越好。
$$one-error=\frac{1}{m}.\sum _{i=1}^{m}g((\arg \underset{y\in Y}{\max }f(x_i,y))\notin Y_i)$$
$$g(x)=\{\begin{array}{ll}0& \text{x为假}\\ 1& \text{x为真}\end{array}$$

2.3 覆盖率（Coverage）

覆盖率评价我们平均还差多远，在排序列表中向下，直接覆盖了所有与这个样本相关的标签。覆盖率越小，预测结果越好。
$$coverage=\frac{1}{m}.\sum _{i=1}^m\underset{y\in Y_i}{\max }ran{k}_f(x_i,y)-1$$
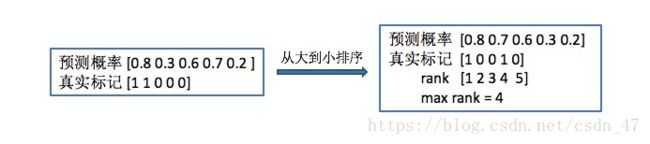
​ 举个例子来解释公式中的max rank。图左边为一个样本的预测概率和真实标记，将预测概率从大到小排序，对应的真实标记也跟着排序，排序后真实标记中从左往右，最后一个标记为1的情绪类别对应的排名为4，因此max rank = 4。

2.4 排序损失（Ranking loss，RL）

表示有多少不相关的标签排序高于相关的标签。排序损失用来表示在结果排序中，不属于相关标签集中的项目被排在了属于相关标签集中项目的概率的平均。排序损失越小，预测结果越好。
$$\begin{array}{r}RL=\frac{1}{m}.\sum _{i=1}^m\frac{1}{|Y_i||\overline{Y_i}|}|\{(y_1,y_2)|f(x_i,y_1)\le f(x_i,y_2),(y_1,y_2)\in Y_i\times \overline{Y_i}\}|\end{array}$$

$\overline{Y_i}$ 是 $Y_i$ 相对于所有类别标签集合L的补集。

2.5 平均精度（Average precision，AVP）

在所有的预测结果排序中，排序排在相关标签集的标签前面，且属于相关标签集的概率，该指标反映了分类标签的平均精确度。这个指标最初用于信息检索（IR）系统，用来评估检索的文本排序性能。平均精度越大，预测效果越好。
$$\begin{array}{rl}AVG& =\frac{1}{m}\sum _{i=1}^m\frac{1}{|Y_i|}\times \sum _{y\in Y_i}\frac{|y^{‘}|ran{k}_f(x_i,y^{‘})\le ran{k}_f(x_i,y),y^{‘}\in Y_i)|}{ran{k}_f(x_i,y)}\end{array}$$
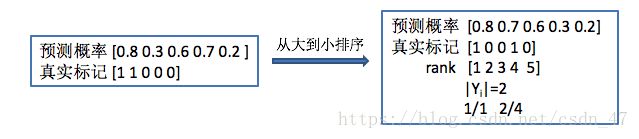
举个例子来解释公式。还是刚刚那个样例，Yi表示第i个样本中真实标记为1的个数，这里等于2。这一部分的公式，分母表示标记为1的情绪类别所对应的排名，分子表示小于等于该排名的情绪类别中标记为1的个数，对于所有标记为1的情绪类别进行计算。比如，第一个1所在的位置rank=1，因此分母=1，排名比它小且标计为1的个数为1，因此值为1. 第二个1所在的位置rank=4，因此分母=4，排名比它小且标计为1的个数为2，因此值为2/4.

3 ML-KNN

给定样本x和它的类别集合 $Y\subseteq \Omega$ ,令 $y_x$ 表示 $x$ 的类别向量，如果标签 $\iota \in \Omega$ ,那么 $y_x(\iota )(\iota \in \Omega )$ 的值为1，否则为0。

令N(x)表示样本x在训练集中的K近邻，根据这些邻居的标签集，可以计算属于第 $\iota$ 个类别的邻居个数，用公式表示为：
$$C_x(\iota )=\sum _{a\in N(x)}{y}_a(\iota )$$

对于一个测试样本 $t$ ，用最大后验概率原则（MAP）决定测试样本是否有类别标签 $\iota$ ，使用如下公式：
$$\begin{array}{rl}{y}_t(L)& =\arg \underset{b\in \{0,1\}}{\max }p(H_b^L|E_{C_t(L)}^L)\\ & =\arg \underset{b\in \{0,1\}}{\max }p(H_b^L).p(E_{C_t(L)}^L|H_b^L)\end{array}$$

其中，$H_1^L$ 表示t中包含情绪标签L，$H_0^L$ 表示t不包含情绪标签L。$E_j^{L}j\in \{0,1,\dots ,k\}$ 表示在 $t$ 的 $k$ 近邻中，有 $j$ 个样本有标签 $L$ 。$C_t^L$ 用来计算 $t$ 的 $k$ 个近邻中含有情绪 $L$ 的近邻个数，$C_t^L={\sum }_{a\in N(t)}{y}_a(L)$ 。先验概率 $p(H_b^L)$ 和后验概率 $p(E_{C_t(L)}^L|H_b^L$ 可以从训练集中计算频度得到。具体的ML-KNN算法过程如图所示：

图片中，s为平滑参数，可被设为1。$r_t$ 是一个真实值向量，用来排序 $\Omega$ 中的标签。$c[j]$ 统计训练集样本中，满足自己含有标签 $\iota$,且它的 $K$ 近邻正好有j个标签 $l$ 这两个条件的样本的个数。$c‘[j]$ 统计训练集样本中满足自己不含有标签 $\iota$ , 且它的 $K$ 近邻正好有 $j$ 个标签ι这两个条件的样本的个数。

4 代码实现

https://github.com/hinanmu/MLKNN