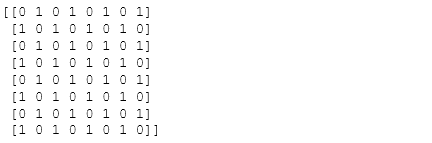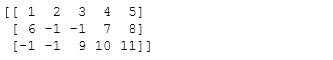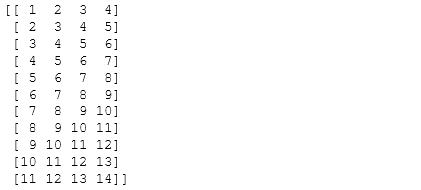Numpy练习
100道NumPy Exercise题
https://github.com/rougier/numpy-100/blob/master/100_Numpy_exercises.ipynb
- 1.导包查看numpy
import numpy as np
print(np.__version__)
![]()
- 2.创建全0的数组,并查看数组占用内存大小
a=np.zeros(10)
print('%d bytes'%(a.size*a.itemsize))
Z = np.zeros((10,10))
print("%d bytes" % (Z.size * Z.itemsize))
- 3.创建一个0~49的数组
Z = np.arange(50)
# 修改数组中的值
Z[3:5]=99
print(Z)
# 数组首尾倒序
Z = Z[::-1]
print(Z)
- 4.数组改变形状reshape
Z = np.arange(9).reshape(3,3)
print(Z)
- 5.生成10*10的数组,并输出最小和最大值
Z = np.random.random((10,10))
Zmin, Zmax = Z.min(), Z.max()
print(Zmin, Zmax)
![]()
- 6.创建10*10的二维全1数组,让除边界以外的全为0
Z = np.ones((10,10))
# 让除边界以外的全为0
Z[1:-1,1:-1] = 0
print(Z)
- 7.创建5*5的全1矩阵,设置矩阵的边界为0
Z = np.ones((5,5))
#设置矩阵的边界为0
Z = np.pad(Z, pad_width=1, mode='constant', constant_values=0)
print(Z)
- 8.创建对角矩阵 对角线上取值1,2,3,4
Z=np.diag((1,2,3,4))
print(Z)
- 9.设置5*5矩阵对角线以下为1,2,3,4
Z = np.diag(1+np.arange(4),k=-1)
print(Z)
- 10.创建一个8*8的棋盘状矩阵
Z = np.zeros((8,8),dtype=int)
Z[1::2,::2] = 1 #行数1开始~最后(每次间隔2),列数0开始~最后列(间隔2)
Z[::2,1::2] = 1
print(Z)
- 11.创建一个8*8的棋盘状矩阵–使用tile对已有的数组进行延展
Z = np.tile( np.array([[0,1],[1,0]]), (4,4))
print(Z)
- 12.对一个5*5的矩阵进行标准化
Z = np.random.random((5,5))
Z = (Z - np.mean (Z)) / (np.std (Z))
print(Z)
- 13.矩阵的乘积
Z = np.dot(np.arange(15).reshape(5,3), np.ones((3,4)))
print(Z)
# Alternative solution, in Python 3.5 and above
Z = np.arange(15).reshape(5,3) @ np.ones((3,4))
print(Z)
- 14.返回一个flatten矩阵的元素的index的横竖索引(x,y)
#numpy.unravel_index(indices, dims, order=‘C’)
#Converts a flat index or array of flat indices into a tuple of coordinate arrays.
# 返回一个flatten矩阵的元素的index的横竖索引(x,y)
print(np.unravel_index(16,(4,5)))# 表示如果把一个4*5的矩阵变成一个扁平的一维数组,索引16在原矩阵中的行坐标和列坐标为3,1
#16=3*5+1
# 返回flat array中索引为100元素在维度(6,7,8)的矩阵中所在的下标
print(np.unravel_index(100,(6,7,8)))
loc_indexs=np.unravel_index([22, 41, 37], (7,6))
print(loc_indexs)
# 22=3*6+4 横竖坐标(3,4)
# 41=6*6+5
# 37=6*6+1
- 15.Create a custom dtype that describes a color as four unsigned bytes (RGBA)
color = np.dtype([("r", np.ubyte, 1),
("g", np.ubyte, 1),
("b", np.ubyte, 1),
("a", np.ubyte, 1)])
print(color)
![]()
- 16.下面代码结果?
print(sum(range(5),-1))
print(sum(range(5),-3))
- 17.How to round away from zero a float array ?
# numpy.copysign(x1, x2, /, out=None, *, where=True, casting='same_kind',
# order='K', dtype=None, subok=True[, signature, extobj])
# Change the sign of x1 to that of x2, element-wise.
Z = np.random.uniform(-10,10,10)
print(Z)
print(np.copysign(np.ceil(np.abs(Z)), Z))
- 18.数组取交集
Z1 = np.random.randint(0,10,10)
Z2 = np.random.randint(0,10,10)
print(np.intersect1d(Z1,Z2))
![]()
- 19.输出昨天、今天、明天的日期
yesterday = np.datetime64('today', 'D') - np.timedelta64(1, 'D')
today = np.datetime64('today', 'D')
tomorrow = np.datetime64('today', 'D') + np.timedelta64(1, 'D')
print('yesterday:',yesterday,'today:',today,'tomorrow:',tomorrow)
![]()
- 20.判断今天是不是工作日
print(np.is_busday(np.datetime64('today', 'D')))#True
# numpy.busday_count(begindates, enddates, weekmask='1111100', holidays=[], busdaycal=None, out=None)
# 计算两个日期之间的工作日天数
print(np.busday_count('2018-01-01','2018-12-31'))# 260 days
- 21.获取2019年2月所有的天
Z = np.arange('2019-02', '2019-03', dtype='datetime64[D]')
print(Z)
- 22.计算((A+B)*(-A/2)) in place (without copy)
A = np.ones(3)*1
B = np.ones(3)*2
C = np.ones(3)*3
np.add(A,B,out=B)
np.divide(A,2,out=A)
np.negative(A,out=A)
np.multiply(A,B,out=A)
print(A)
![]()
- 23.用5种不同的方法提取随机数组中的整数
Z = np.random.uniform(0,10,10)
print (Z - Z%1)
print (np.floor(Z))
print (np.ceil(Z)-1)
print (Z.astype(int))
print (np.trunc(Z))
- 24.创建一个5x5 矩阵 with row values ranging from 0 to 4
Z = np.zeros((5,5))
Z += np.arange(5)# Z矩阵的每一行都加上[0 1 2 3 4 ]
print(Z)
- 25.利用生成器产生10个整数,组成数组
def generate():
for x in range(10):
yield x
Z = np.fromiter(generate(),dtype=float,count=-1)
print(Z)
![]()
- 26.创建一个从0~1之间的10个数,不包括两端端点
Z = np.linspace(0,1,11,endpoint=False)[1:]
print(Z)
- 27.样对一个小的数组进行累加求和,要求比np.sum更快
Z = np.arange(10)
np.add.reduce(Z)
![]()
- 28.比较两个矩阵的相似性
A = np.random.randint(0,2,5)
B = np.random.randint(0,2,5)
# 假定两个矩阵相同形状,可以容忍相似度存在一定的差异
# numpy.allclose(a, b, rtol=1e-05, atol=1e-08, equal_nan=False)[source]
# Returns True if two arrays are element-wise equal within a tolerance.
equal = np.allclose(A,B)
print(equal)
# 确定的比较两个矩阵的形状和对值进行逐一比较,零容忍:要么完全相同,要么不同
equal = np.array_equal(A,B)
print(equal)
- 29.创建一个不可修改的数组,只读
Z = np.zeros(10)
Z.flags.writeable = False#设置不可修改
Z[0] = 1#对数组进行修改,会报错
- 30.创建一个10x2的矩阵(默认直角坐标系-笛卡尔坐标系),转换成极坐标系–牛顿创立
Z = np.random.random((10,2))
X,Y = Z[:,0], Z[:,1]
R = np.sqrt(X**2+Y**2)# 极坐标系半径
T = np.arctan2(Y,X)#旋转角度
print(R)
print(T)
- 31.创建一个10个数的数组,将最大值替换成0
Z = np.random.random(10)
print(Z)
Z[Z.argmax()] = 0#argmax:返回最大值所在下标index,argmin返回最小值的index
print(Z)
- 32.创建(x,y)坐标,覆盖[0,1]x[0,1]的正方形区域
Z = np.zeros((5,5), [('x',float),('y',float)])#自定义dtype
print(Z)
print(Z['x'])
Z['x'], Z['y'] = np.meshgrid(np.linspace(0,1,5),
np.linspace(0,1,5))
print(Z['y'])#y横向排列,每一行中数值相同,x纵向排列,每一列中数值相同
print(Z)
- 32.构建柯西矩阵Cauchy matrix C (Cij =1/(xi - yj))
X = np.arange(8)
Y = X + 0.5
C = 1.0 / np.subtract.outer(X, Y)
print(np.linalg.det(C))#计算矩阵行列式
![]()
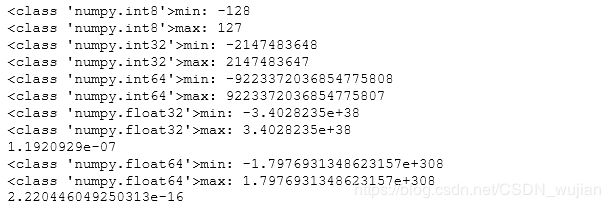
- 33.打印numpy中标量类型所能表示的最大值和最小值
for dtype in [np.int8, np.int32, np.int64]:
print(str(dtype)+'min:',np.iinfo(dtype).min)
print(str(dtype)+'max:',np.iinfo(dtype).max)
# int8[-128,127]
# int32[-2147483648,2147483647]
# int32[-9223372036854775808,9223372036854775807]
for dtype in [np.float32, np.float64]:
print(str(dtype)+'min:',np.finfo(dtype).min)
print(str(dtype)+'max:',np.finfo(dtype).max)
print(np.finfo(dtype).eps)#float所能表示的精度
- 34.打印数组中的所有的值
np.set_printoptions(threshold=np.nan)
Z = np.zeros((16,16))
print(Z)
- 35.从一个数组中找出与给定标量值最相近的值
Z = np.arange(100)
v = np.random.uniform(0,100)
print('v:',v)
index = (np.abs(Z-v)).argmin()
print(Z[index])
- 36.Create a structured array representing a position (x,y) and a color (r,g,b)
Z = np.zeros(10, [ ('position', [('x', float, 1),('y', float, 1)]),
('color', [('r', float, 1),('g', float, 1),('b', float, 1)])
]
)
print(Z)
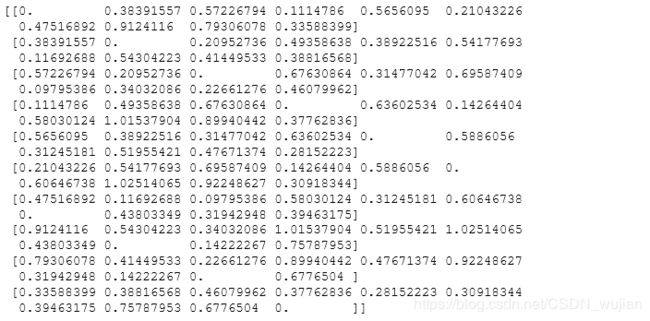
- 37.100x2维的矩阵,计算点与点之间的距离,类似于求两两之间的相似度
Z = np.random.random((10,2))
X,Y = np.atleast_2d(Z[:,0], Z[:,1])
D = np.sqrt( (X-X.T)**2 + (Y-Y.T)**2)
print(D)
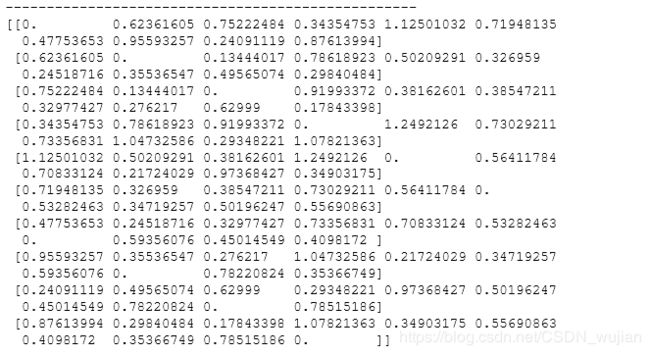
print('-'*50)
# Much faster with scipy
import scipy
import scipy.spatial
Z = np.random.random((10,2))
D = scipy.spatial.distance.cdist(Z,Z)
print(D)
- 38.把float32的数组转成int32的数组,without copy
Z = np.arange(10, dtype=np.float32)
Z = Z.astype(np.int32, copy=False)
print(Z)
![]()
- 39.np读取文件数据
from io import StringIO
# Fake file
s = StringIO("""1, 2, 3, 4, 5\n
6, , , 7, 8\n
, , 9,10,11\n""")
Z = np.genfromtxt(s, delimiter=",", dtype=np.int)
print(Z
- 40.np.ndenumerate与Python中的enumerate相类似
Z = np.arange(9).reshape(3,3)
for index, value in np.ndenumerate(Z):
print(index, value)
print('-'*50)
for index in np.ndindex(Z.shape):
print(index, Z[index])
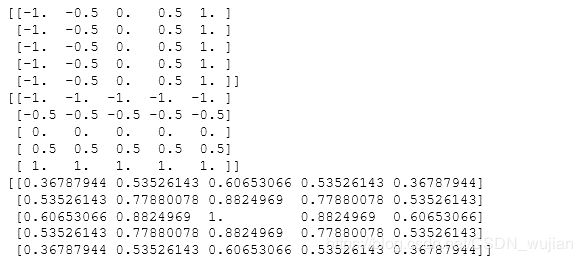
- 41.生成2D的高斯分布数组
X, Y = np.meshgrid(np.linspace(-1,1,5), np.linspace(-1,1,5))
print(X)
print(Y)
D = np.sqrt(X*X+Y*Y)
sigma, mu = 1.0, 0.0
G = np.exp(-( (D-mu)**2 / ( 2.0 * sigma**2 ) ) )#正态分布概率密度函数
print(G)
- 42.np.put随机把p个元素放置在2D array中
n = 10
p = 3
Z = np.zeros((n,n))
# numpy.put(a, ind, v, mode='raise')
# Replaces specified elements of an array with given values.
np.put(Z, np.random.choice(range(n*n), p, replace=False),2)
print(Z)
- 43.矩阵的每一行减去该行的均值
X = np.random.rand(3, 5)#3x5的矩阵
# Recent versions of numpy
Y = X - X.mean(axis=1, keepdims=True)
# 或者
# Older versions of numpy
Y = X - X.mean(axis=1).reshape(-1, 1)
print(Y)
- 44.对数组按照指定列进行排序
Z = np.random.randint(0,10,(3,3))
print(Z)
print(Z[Z[:,1].argsort()])#对数组按照第2列进行排序
- 45.判断矩阵是否存在空列
Z = np.random.randint(0,3,(3,10))
print(Z)
# np.array.any()是或操作,将np.array中所有元素进行或操作,然后返回True或False
# np.array.all()是与操作,将np.array中所有元素进行与操作,然后返回True或False
print((~Z.any(axis=0)).any())
- 46.找出数组中与给定值最相近的数
Z = np.random.uniform(0,1,10)
print(Z)
z = 0.5
# ndarray.flat 将数组转换为1-D的迭代器 /
# flat返回的是一个迭代器,可以用for访问数组每一个元素
m = Z.flat[np.abs(Z - z).argmin()]
print(m)
# ndarray.flatten(order=’C’)
# Return a copy of the array collapsed into one dimension.
# 将数组的副本转换为一个维度,并返回
# order:{‘C’,‘F’,‘A’,‘K’}
# 可选参数,order:{‘C’,‘F’,‘A’,‘K’}
# ‘C’:C-style,行序优先
# ‘F’:Fortran-style,列序优先
# ‘A’:if a is Fortran contiguous in memory ,flatten in column_major order
# ‘K’:按照元素在内存出现的顺序进行排序
# 默认为’C’
- 46.运用迭代器计算13数组和31数组的和
A = np.arange(3).reshape(3,1)
B = np.arange(3).reshape(1,3)
it = np.nditer([A,B,None])
for x,y,z in it: z[...] = x + y
print(it.operands[2])
- 47.np.nditer: numpy array自带的迭代器
# it = np.nditer(x, flags=['multi_index'], op_flags=['readwrite'])
# numpy array自带的迭代器,multi_index:多重索引[输出:就是数组索引号(0,0)(0,1)等];
# readwrite:对x有可读可写的权限;iternext():控制下一次迭代,如果没有这个控制下一次,就一直在一个索引值上操作;挺好用。
a=np.arange(0,60,5).reshape(3,4)
it=np.nditer(a,flags=['multi_index'],op_flags=['readwrite'])
while not it.finished:
print(it.multi_index)#输出迭代器索引
it.iternext()
- 48.Create an array class that has a name attribute (★★☆)
class NamedArray(np.ndarray):
def __new__(cls, array, name="no name"):
obj = np.asarray(array).view(cls)
obj.name = name
return obj
def __array_finalize__(self, obj):
if obj is None: return
self.info = getattr(obj, 'name', "no name")
Z = NamedArray(np.arange(10), "range_10")
print(Z.name)
![]()
- 49.Consider a given vector, how to add 1 to each element indexed by a second vector (be careful with repeated indices)? (★★★)
Z = np.ones(10)
# numpy.random.randint
# low、high、size三个参数。默认high是None,如果只有low,那范围就是[0,low)。如果有high,范围就是[low,high)。
I = np.random.randint(0,len(Z),20)
Z += np.bincount(I, minlength=len(Z))
print(Z)
# 关于numpy.bincount详解:https://blog.csdn.net/xlinsist/article/details/51346523
# bin的数量比x中的最大值大1,每个bin给出了它的索引值在x中出现的次数
# Another solution
np.add.at(Z, I, 1)
print(Z)
- 50.How to accumulate elements of a vector (X) to an array (F) based on an index list (I)? (★★★)
X = [1,2,3,4,5,6]
I = [1,3,9,3,4,1]
F = np.bincount(I,X)#X为权重weight数组,out[n] += weight[i]
print(F)
![]()
- 51.Considering a (w,h,3) image of (dtype=ubyte), compute the number of unique colors (★★★)
w,h = 16,16
I = np.random.randint(0,2,(h,w,3)).astype(np.ubyte)
#Note that we should compute 256*256 first.
#Otherwise numpy will only promote F.dtype to 'uint16' and overfolw will occur
F = I[...,0]*(256*256) + I[...,1]*256 +I[...,2]
n = len(np.unique(F))
print(n)
![]()
- 52.四维矩阵,通过最后两个轴快速求和
A = np.random.randint(0,10,(3,4,3,4))
# solution by passing a tuple of axes (introduced in numpy 1.7.0)
sum = A.sum(axis=(-2,-1))
print(sum)
# solution by flattening the last two dimensions into one
# (useful for functions that don't accept tuples for axis argument)
sum = A.reshape(A.shape[:-2] + (-1,)).sum(axis=-1)
print(sum)
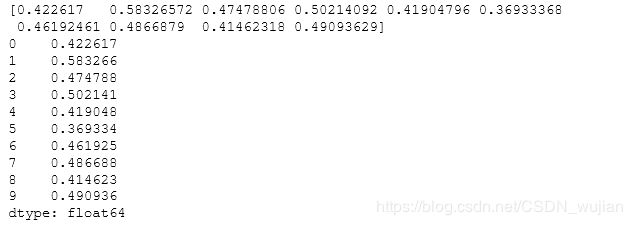
- 53.Considering a one-dimensional vector D, how to compute means of subsets of D using a vector S of same size describing subset indices? (★★★)
D = np.random.uniform(0,1,100)# 均匀分布[0,1),左闭右开,size=100
S = np.random.randint(0,10,100)
D_sums = np.bincount(S, weights=D)
D_counts = np.bincount(S)
D_means = D_sums / D_counts
print(D_means)
# Pandas solution as a reference due to more intuitive code
import pandas as pd
print(pd.Series(D).groupby(S).mean())
- 54.获取矩阵点乘后的对角线元素值
A = np.random.uniform(0,1,(5,5))
B = np.random.uniform(0,1,(5,5))
# np.diag(array)
# array是一个1维数组时,结果形成一个以一维数组为对角线元素的矩阵
# array是一个二维矩阵时,结果输出矩阵的对角线元素
# Slow version
np.diag(np.dot(A, B))
# Fast version
np.sum(A * B.T, axis=1)
# Faster version
np.einsum("ij,ji->i", A, B)
# numpy.einsum(subscripts, *operands, out=None, dtype=None, order='K', casting='safe', optimize=False)
# subscripts用于指定计算模式,operands用于指定操作数
![]()
- 55.在向量[1, 2, 3, 4, 5]的每个值之间放3个0
Z = np.array([1,2,3,4,5])
nz = 3
Z0 = np.zeros(len(Z) + (len(Z)-1)*(nz))
Z0[::nz+1] = Z#把Z中原来的值放入Z0中,每间隔4
print(Z0)
![]()
- 56.一个553的数组如何与5*5的数组相乘
A = np.ones((5,5,3))
B = 2*np.ones((5,5))
print(A * B[:,:,None])#由于维度不够,在第三维上使用None填充
- 57.交换数组的两行
A = np.arange(25).reshape(5,5)
A[[0,1]] = A[[1,0]]
print(A)
- 58.交换数组的两列
A = np.arange(25).reshape(5,5)
A[:,[0,1]]=A[:,[1,0]]
print(A)
- 59.Consider a set of 10 triplets describing 10 triangles (with shared vertices), find the set of unique line segments composing all the triangles (★★★)
faces = np.random.randint(0,100,(10,3))
# np.roll(a, shift, axis=None)将a,沿着axis的方向,滚动shift长度
# numpy.repeat(a, repeats, axis=None)[source]
# Repeat elements of an array.
F = np.roll(faces.repeat(2,axis=1),-1,axis=1)
F = F.reshape(len(F)*3,2)
F = np.sort(F,axis=1)
G = F.view( dtype=[('p0',F.dtype),('p1',F.dtype)] )
G = np.unique(G)
print(G)
- 60.Given an array C that is a bincount, how to produce an array A such that np.bincount(A) == C? (★★★)
C = np.bincount([1,1,2,3,4,4,6])
print(np.arange(len(C)))
print(C)
A = np.repeat(np.arange(len(C)), C)
print(A)
- 61.在数组中利用滑动窗口计算移动平均值 (★★★)
def moving_average(a, n=3) :
ret = np.cumsum(a, dtype=float)
ret[n:] = ret[n:] - ret[:-n]
return ret[n - 1:] / n
Z = np.arange(20)
print(moving_average(Z, n=3))
![]()
- 62.Consider a one-dimensional array Z, build a two-dimensional array whose first row is (Z[0],Z[1],Z[2]) and each subsequent row is shifted by 1 (last row should be (Z[-3],Z[-2],Z[-1]) (★★★)
from numpy.lib import stride_tricks
# as_strided creates a view into the array given the exact strides and shape.
# This means it manipulates the internal data structure of ndarray and,
# if done incorrectly, the array elements can point to invalid memory and can corrupt results or crash your program.
# itemsize输出array元素的字节数:int:4,float:8
def rolling(a, window):
shape = (a.size - window + 1, window)
strides = (a.itemsize, a.itemsize)#(4,4)
return stride_tricks.as_strided(a, shape=shape, strides=strides)
Z = rolling(np.arange(10), 3)
print(Z)
- 63.Consider an array Z = [1,2,3,4,5,6,7,8,9,10,11,12,13,14],how to generate an array R = [[1,2,3,4], [2,3,4,5], [3,4,5,6], …, [11,12,13,14]]? (★★★)
from numpy.lib import stride_tricks
Z = np.arange(1,15,dtype=np.uint32)
R = stride_tricks.as_strided(Z,(11,4),(4,4))
print(R)
- 64.Extract all the contiguous 3x3 blocks from a random 10x10 matrix (★★★)
Z = np.random.randint(0,5,(10,10))
n = 3
i = 1 + (Z.shape[0]-3)
j = 1 + (Z.shape[1]-3)
C = stride_tricks.as_strided(Z, shape=(i, j, n, n), strides=Z.strides + Z.strides)
print(C)
- 64.boolean型数组取反,或者数组对元素取相反数
import numpy as np
Z = np.random.randint(0,2,100)
np.logical_not(Z, out=Z)
Z = np.random.uniform(-1.0,1.0,20)
np.negative(Z, out=Z)#对数组元素取反
- 65.计算点p到各条直线(p0,p1)的距离
def distance(P0, P1, p):
T = P1 - P0
L = (T**2).sum(axis=1)
U = -((P0[:,0]-p[...,0])*T[:,0] + (P0[:,1]-p[...,1])*T[:,1]) / L
U = U.reshape(len(U),1)
D = P0 + U*T - p
return np.sqrt((D**2).sum(axis=1))
P0 = np.random.uniform(-10,10,(10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10,10,( 1,2))
print(distance(P0, P1, p))
- 66.计算多个点到多条直线的距离
# based on distance function from previous question
P0 = np.random.uniform(-10, 10, (10,2))
P1 = np.random.uniform(-10,10,(10,2))
p = np.random.uniform(-10, 10, (5,2))#5个点
print(np.array([distance(P0,P1,p_i) for p_i in p]))
- 67.Consider an arbitrary array, write a function that extract a subpart with a fixed shape and centered on a given element (pad with a fill value when necessary) (★★★)
Z = np.random.randint(0,10,(10,10))
shape = (5,5)
fill = 0
position = (1,1)#以index(1,1)为中心,从Z矩阵中抽取一个5*5的矩阵,不足部分填充0
R = np.ones(shape, dtype=Z.dtype)*fill
P = np.array(list(position)).astype(int)
Rs = np.array(list(R.shape)).astype(int)
Zs = np.array(list(Z.shape)).astype(int)
R_start = np.zeros((len(shape),)).astype(int)
R_stop = np.array(list(shape)).astype(int)
Z_start = (P-Rs//2)
Z_stop = (P+Rs//2)+Rs%2
R_start = (R_start - np.minimum(Z_start,0)).tolist()
Z_start = (np.maximum(Z_start,0)).tolist()
R_stop = np.maximum(R_start, (R_stop - np.maximum(Z_stop-Zs,0))).tolist()
Z_stop = (np.minimum(Z_stop,Zs)).tolist()
r = [slice(start,stop) for start,stop in zip(R_start,R_stop)]
z = [slice(start,stop) for start,stop in zip(Z_start,Z_stop)]
R[r] = Z[z]
print(Z)
print(R)
- 68.矩阵分解、计算矩阵的秩
Z = np.random.uniform(0,1,(10,10))
U, S, V = np.linalg.svd(Z) # Singular Value Decomposition
rank = np.sum(S > 1e-10)
print(rank)
![]()
- 69.在数组中找出出现次数最多的值
Z = np.random.randint(0,10,50)
print(np.bincount(Z).argmax())
![]()
- 70.创建一个对称的矩阵
class Symetric(np.ndarray):
def __setitem__(self, index, value):
i,j = index
super(Symetric, self).__setitem__((i,j), value)
super(Symetric, self).__setitem__((j,i), value)
def symetric(Z):
return np.asarray(Z + Z.T - np.diag(Z.diagonal())).view(Symetric)
S = symetric(np.random.randint(0,10,(5,5)))
S[2,3] = 42
print(S)
- 71.Consider a set of p matrices wich shape (n,n) and a set of p vectors with shape (n,1).How to compute the sum of of the p matrix products at once? (result has shape (n,1)) (★★★)
p, n = 10, 20
M = np.ones((p,n,n))
V = np.ones((p,n,1))
# 张量乘积tensordot()将两个多维数组a和b指定轴上的对应元素相乘并求和,它是最一般化的乘积运算函数。
S = np.tensordot(M, V, axes=[[0, 2], [0, 1]])
print(S)
# It works, because:
# M is (p,n,n)
# V is (p,n,1)
# Thus, summing over the paired axes 0 and 0 (of M and V independently),
# and 2 and 1, to remain with a (n,1) vector.
- 72.Consider a 16x16 array, how to get the block-sum (block size is 4x4)? (★★★)
Z = np.ones((16,16))
k = 4
# 先横着把行的四个相加,在把竖着列相加
S = np.add.reduceat(np.add.reduceat(Z, np.arange(0, Z.shape[0], k), axis=0),
np.arange(0, Z.shape[1], k), axis=1)
print(S)
- 73.How to implement the Game of Life using numpy arrays? (★★★)
def iterate(Z):
# Count neighbours
N = (Z[0:-2,0:-2] + Z[0:-2,1:-1] + Z[0:-2,2:] +
Z[1:-1,0:-2] + Z[1:-1,2:] +
Z[2: ,0:-2] + Z[2: ,1:-1] + Z[2: ,2:])
# Apply rules
birth = (N==3) & (Z[1:-1,1:-1]==0)
survive = ((N==2) | (N==3)) & (Z[1:-1,1:-1]==1)
Z[...] = 0
Z[1:-1,1:-1][birth | survive] = 1
return Z
Z = np.random.randint(0,2,(50,50))
for i in range(100): Z = iterate(Z)
print(Z)
- 74.How to get the n largest values of an array (★★★)
Z = np.arange(10000)
np.random.shuffle(Z)
n = 5
# Slow
print (Z[np.argsort(Z)[-n:]])
# Fast
print (Z[np.argpartition(-Z,n)[:n]])
- 75.给定多个数组,构建一个笛卡尔积矩阵(元素之间两两组合) (★★★)
def cartesian(arrays):
arrays = [np.asarray(a) for a in arrays]
shape = (len(x) for x in arrays)
ix = np.indices(shape, dtype=int)
ix = ix.reshape(len(arrays), -1).T
for n, arr in enumerate(arrays):
ix[:, n] = arrays[n][ix[:, n]]
return ix
print (cartesian(([1, 2, 3], [4, 5], [6, 7])))
- 76.How to create a record array from a regular array? (★★★)
Z = np.array([("Hello", 2.5, 3),
("World", 3.6, 2)])
R = np.core.records.fromarrays(Z.T,
names='col1, col2, col3',
formats = 'S8, f8, i8')
print(R)
[(b’Hello’, 2.5, 3) (b’World’, 3.6, 2)]
- 76.计算一个超大向量的三次方
# np.random.rand返回一个或一组服从“0~1”均匀分布的随机样本值。随机样本取值范围是[0,1),不包括1。
x = np.random.rand(5000)#生成5*10^7个[0,1)之间的数
# timeit准确测量小段代码的执行时间
# ipython中以%开头的叫做line magic, 这种类型的指令只能作用于一行代码,默认是可以不带百分号使用的。
# 以%%开头的叫做cell magic, 这种类型的指令只能作用于代码块。
%timeit np.power(x,3)
%timeit x*x*x
%timeit np.einsum('i,i,i->i',x,x,x)
748 µs ± 53.8 µs per loop (mean ± std. dev. of 7 runs, 1000 loops each)
22 µs ± 3.77 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
30.2 µs ± 2.17 µs per loop (mean ± std. dev. of 7 runs, 10000 loops each)
- 77.A矩阵83,B矩阵22,找出A矩阵中包含所有B矩阵值的行,不考虑顺序 (★★★)
A = np.random.randint(0,5,(8,3))
B = np.random.randint(0,5,(2,2))
print(A)
print(B)
C = (A[..., np.newaxis, np.newaxis] == B)
rows = np.where(C.any((3,1)).all(1))[0]
print('rows:',rows)
- 78.Considering a 10x3 matrix, extract rows with unequal values (e.g. [2,2,3]) (★★★)
Z = np.random.randint(0,4,(10,3))
print(Z)
# solution for arrays of all dtypes (including string arrays and record arrays)
E = np.all(Z[:,1:] == Z[:,:-1], axis=1)
U = Z[~E]
print(U)
# soluiton for numerical arrays only, will work for any number of columns in Z
U = Z[Z.max(axis=1) != Z.min(axis=1),:]
print(U)
- 79.Convert a vector of ints into a matrix binary representation (★★★)
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128])
B = ((I.reshape(-1,1) & (2**np.arange(8))) != 0).astype(int)
print(B[:,::-1])
# another 方法
I = np.array([0, 1, 2, 3, 15, 16, 32, 64, 128], dtype=np.uint8)
print(np.unpackbits(I[:, np.newaxis], axis=1))
- 80.Given a two dimensional array, how to extract unique rows? (★★★)
Z = np.random.randint(0,2,(6,3))
T = np.ascontiguousarray(Z).view(np.dtype((np.void, Z.dtype.itemsize * Z.shape[1])))
_, idx = np.unique(T, return_index=True)
uZ = Z[idx]
print(uZ)
# Author: Andreas Kouzelis
# NumPy >= 1.13
uZ = np.unique(Z, axis=0)
print(uZ)
- 81.Considering 2 vectors A & B, write the einsum equivalent of inner, outer, sum, and mul function (★★★)
A = np.random.uniform(0,1,10)
B = np.random.uniform(0,1,10)
np.einsum('i->', A) # np.sum(A)
np.einsum('i,i->i', A, B) # A * B
np.einsum('i,i', A, B) # np.inner(A, B)
np.einsum('i,j->ij', A, B) # np.outer(A, B)
- 82.Considering a path described by two vectors (X,Y), how to sample it using equidistant samples (★★★)?
phi = np.arange(0, 10*np.pi, 0.1)
a = 1
x = a*phi*np.cos(phi)
y = a*phi*np.sin(phi)
dr = (np.diff(x)**2 + np.diff(y)**2)**.5 # segment lengths
r = np.zeros_like(x)
r[1:] = np.cumsum(dr) # integrate path
r_int = np.linspace(0, r.max(), 200) # regular spaced path
x_int = np.interp(r_int, r, x) # integrate path
y_int = np.interp(r_int, r, y)
- 83.Given an integer n and a 2D array X, select from X the rows which can be interpreted as draws from a multinomial distribution with n degrees, i.e., the rows which only contain integers and which sum to n. (★★★)
X = np.asarray([[1.0, 0.0, 3.0, 8.0],
[2.0, 0.0, 1.0, 1.0],
[1.5, 2.5, 1.0, 0.0]])
n = 4
M = np.logical_and.reduce(np.mod(X, 1) == 0, axis=-1)
M &= (X.sum(axis=-1) == n)
print(X[M])
[[2. 0. 1. 1.]]
- 84.# Compute bootstrapped 95% confidence intervals for the mean of a 1D array X (i.e., resample the elements of an array with replacement N times, compute the mean of each sample, and then compute percentiles over the means). (★★★)
X = np.random.randn(100) # random 1D array
N = 1000 # number of bootstrap samples
idx = np.random.randint(0, X.size, (N, X.size))
means = X[idx].mean(axis=1)
confint = np.percentile(means, [2.5, 97.5])
print(confint)
[-0.20332504 0.15369648]