sas统计分析学习笔记(九)——方差分析
1.简介
当数据多于两组时,T检验或者相应的非参数分析不再适应,这时需要使用方差分析。
2.单因素方差分析
零假设为所有组的均值相等,备择假设是不是所有平均数都相等。F=组间方差/组内方差=[组间平方和/(k-1)]/[误差平方和/(n-k)],如果组间差异比组内大,比值将大于1,如果零假设为真,F将等于1。
DATA READING;
INPUT GROUP $ WORDS @@;
DATALINES;
X 700 X 850 X 820 X 640 X 920
Y 480 Y 460 Y 500 Y 570 Y 580
Z 500 Z 550 Z 480 Z 600 Z 610
;
PROC ANOVA DATA=READING;
TITLE "Analysis of Reading Date";
CLASS GROUP;*指定自变量;
MODEL WORDS=GROUP; *指定分析模型;
MEANS GROUP;*计算GROUP的每个水平上的WORDS平均值;
RUN;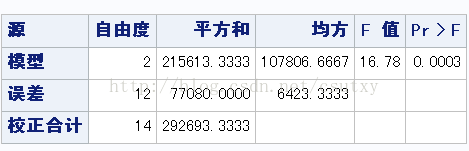
这里,F值为16.78,查表(自由度为2和12),p为0.0003,因此拒绝零假设,得到结论阅读方法存在差异。
当已经知道阅读方法存在差异时,可以找出具体的组间差异,此方法为事后检验或者多重检验。
若要进行事后检验,将检验的选项名放在MEANS的斜杠后,前面列出检验的SAS关键词DUNCAN(duncan多重范围检验)、SNK(student-newman-keuls多重范围检验)、LSD(最小显著差异检验)、TUKEY(tukey学生化范围检验)、SCHEFFE(scheffe多重比较过程)。实际中,如果方差分析不显著,就不进行事后检验,上例中方差分析结果显著存在差异,运用SNK进行事后检验,语句如下:
MEANS GROUP/SNK;
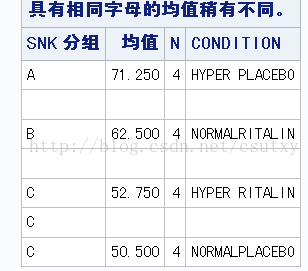
输出结果次序由各组平均数由高到低排列,平均数没有显著差异的一组会被分配到相同字母。本例中,z和y没有显著差异,但都与x有显著差异。
除非特别指定,组间差异检验显著水平默认为0.05,也可以在事后检验的选项后面加上ALPHA=.1或者ALPHA=.01,指定显著水平分别为.1或者.01。当指定scheffe检验的显著水平为.1时,应写成:
MEANS GROUP / SCHEFFE ALPHA=.1;
3.对比检验
进行特定的比较检验,你需要PROC GLM来代替PROC ANOVA。
PROC GLM DATA=READING;
CLASS GROUP;
MODEL WORDS=GROUP;
CONTRAST 'X VS. Y AND Z' GROUP -2 1 1;
CONTRAST 'METHOD Y VS Z' GROUP 0 1 -1;
RUN;
规则为:1.系数之和为0;2.如果没有给CLASS变量设定输出格局,那么系数的顺序必须与CLASS变量的各个水平的字母顺序相匹配。如果为CLASS变量指定了输出格式,那么系数顺序就与格式化的值的顺序一致(通过在PROC GLM中添加选项ORDER = DATA,可以使CLASS变量的各个水平按照数据值排序,而不再是格式化顺序,这样就可以避开设定系数顺序问题了);3.系数0表示在比较检验中不纳入相关的水平;4.负系数对应的水平和正系数对应的水平进行比较。
上面程序,第一个CONTRAST比较了方法x与方法y和z的平均数,第二个只比较了y和z。
从结果可以看到,方法x与方法y、z有显著差异,而方法y和z之间没有显著差异。
4.两个自变量的方差分析
假设同样是对阅读方法进行比较,但一共有15个男性被试和15个女性被试。除了比较阅读方法,还想比较男性和女性的阅读速度是否有区别。
| 组别 | |||
| X | Y | Z | |
| 男性 | 700 | 480 | 500 |
| 850 | 460 | 550 | |
| 820 | 500 | 480 | |
| 640 | 570 | 600 | |
| 920 | 580 | 610 | |
| 女性 | 900 | 590 | 610 |
| 880 | 540 | 660 | |
| 899 | 560 | 525 | |
| 780 | 570 | 610 | |
| 899 | 555 | 645 | |
这个设计中每个单元的被试数目相同,因此成为“平衡设计”,如果模型中有一个以上的自变量,且设计是不平衡的,则不能使用PROC ANOVA,应该使用广义线性模型PROC GLM.
DATA TWOWAY;
LENGTH GROUP GENDER $ 1;
INPUT GROUP $ GENDER $ WORDS @@;
DATALINES;
X M 700 X M 850 X M 820 X M 640 X M 920
Y M 480 Y M 460 Y M 500 Y M 570 Y M 580
Z M 920 Z M 550 Z M 480 Z M 600 Z M 610
X F 900 X F 880 X F 899 X F 780 X F 899
Y F 590 Y F 540 Y F 560 Y F 570 Y F 555
Z F 520 Z F 660 Z F 525 Z F 610 Z F 645
;
PROC ANOVA DATA=TWOWAY;
TITLE "Analysis of reading data";
CLASS GROUP GENDER;
MODEL WORDS=GROUP|GENDER;
MEANS GROUP|GENDER /SNK;
RUN;
GROUP|GENDER|DOSE
GROUP GENDER DOSE GROUP*GENDER GROUP*DOSE GENDER*DOSE GENDER*GROUP *DOSE
下面看看上述程序的部分输出结果:
GROUP*GENDER叫做交互项。如果各个阅读组对男性和女性的差异不同,那么交互效应是显著的,例如,如果男性在A方法比B方法表现好,而女性在B方法比A方法表现好,那么交互作用是显著的。
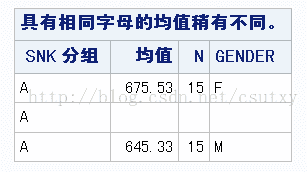
MEANS GROUP|GENDER / SNK;的输出结果部分如下:
第一个表格说明,X与Y、Z有显著差异,第二个说明性别不显著,男女无显著差异。最后还会输出一个各个性别在各个组的平均值表。
5.解释显著地交互作用
下面看一个交互作用显著的例子,有两组小孩,一组正常,一组多动,每组小孩随机分为两组,一组接受安慰剂,一组接受利他林,之后测量每个小孩的活跃度。
| 安慰剂(PLACEBO) | 利他林(RITALIN) | |
| 正常 | 50 | 67 |
| 45 | 60 | |
| 55 | 58 | |
| 52 | 65 | |
| 多动症 | 70 | 51 |
| 72 | 57 | |
| 68 | 48 | |
| 75 | 55 |
DATA RITALIN;
DO GROUP = 'NORMAL','HYPER';
DO DRUG = 'PLACEBO','RITALIN';
DO SUBJ = 1 TO 4;
INPUT ACTIVITY @;
OUTPUT;
END;
END;
END;
DATALINES;
50 45 55 52 67 60 58 65 70 72 68 75 51 57 48 55
;
PROC ANOVA DATA=RITALIN;
TITLE "Activity Study";
CLASS GROUP DRUG;
MODEL ACTIVITY = GROUP|DRUG;
MEANS GROUP|DRUG;
RUN;
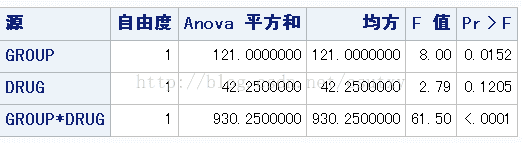
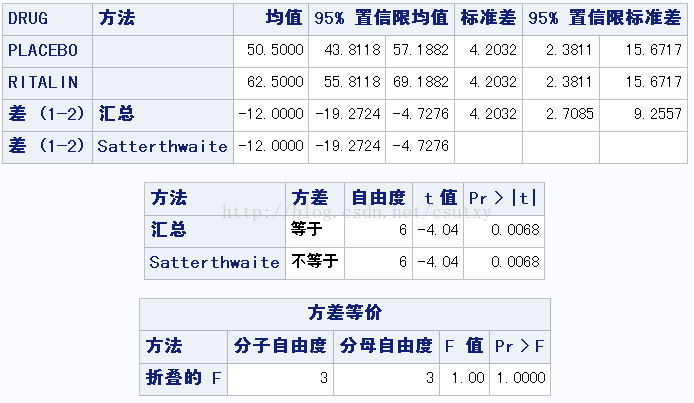
可以看到group*drug的交互作用显著。当交互作用显著时,我们必须非常小心地解释主效应,也就是说必须先理解交互作用的性质,才能进一步考察主效应。
可以利用平均数画一个交互作用图,首先选一个自变量作横轴,然后在另一个自变量每个水平上画出表示因变量平均数的线条。在绘图之前首先通过PROC MEANS 过程创建一个包含着单元格平均数的数据集。
这个图形说明,普通小孩服用利他林活跃度增加,多动症小孩服用利他林活跃度降低。因此在刚刚的方差分析中,关于利他林的检验,两组小孩的数据会相互抵消。如果要考察利他林的真实效果,需要分别考察两组小孩的反应:
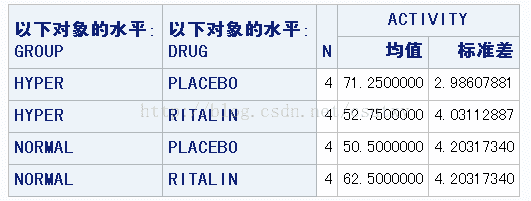
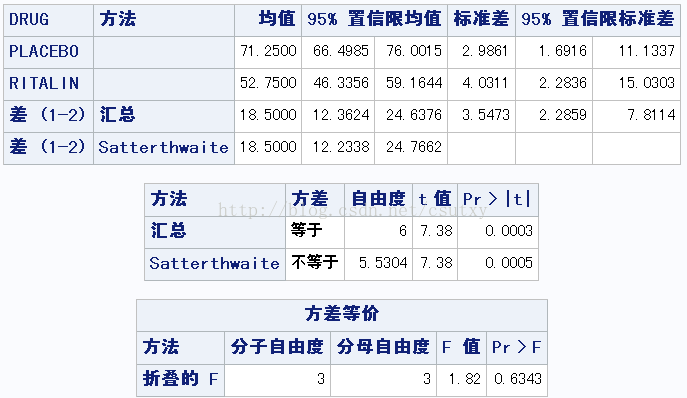
GROUP=HYPER时
从上面可以看到,两组小孩对两组药物的平均数显著不同,但正常组的利他林平均数高于安慰剂,多动组则相反。
还有另一种方法进行上述T检验:将院士变量的每个处理水平相结合,生成一个新的自变量,这样就把两因素ANOVA分解成了单因素ANOVA,可以用串联符号||创建CONDITION变量,在data步骤中加入语句:
CONDITION = GROUP || DRUG;
创建了新变量,共有4个水平,当然也可以使用CATX函数串联两个甚至更多字符串,还可以自由选择连接符:
CONDITION = CATX('-',GROUP,DRUG);
DATA RITALIN;
DO GROUP = 'NORMAL','HYPER';
DO DRUG = 'PLACEBO','RITALIN';
DO SUBJ = 1 TO 4;
INPUT ACTIVITY @;
CONDITION=GROUP||DRUG;
OUTPUT;
END;
END;
END;
DATALINES;
50 45 55 52 67 60 58 65 70 72 68 75 51 57 48 55
;
PROC ANOVA DATA=RITALIN;
TITLE "ONE-WAY ANOVA Ritalin study";
CLASS CONDITION;
MODEL ACTIVITY=CONDITION;
MEANS CONDITION /SNK;
RUN;PROC GLM DATA=RITALIN;
TITLE "ONE-WAY ANOVA Ritalin study";
CLASS CONDITION;
MODEL ACTIVITY=CONDITION;
CONTRAST 'Hyperactive only' CONDITION -1 1 0 0 ;
CONTRAST 'NORMAL only' CONDITION 
6.多因素设计
双因素方差分析的方法可以扩展到任意多自变量的情况,主要在MODEL 和 MEANS步骤用‘|’将各自变量连接起来即可。
7.非平衡设计:PROC GLM
| 甜度水平 | |||
| 1 | 2 | 3 | |
| 香草 | 9 | 8 | 6 |
| 7 | 7 | 5 | |
| 8 | 8 | 7 | |
| 7 | |||
| 巧克力 | 9 | 8 | 4 |
| 9 | 7 | 5 | |
| 7 | 6 | 6 | |
| 7 | 8 | 4 | |
| 8 | 4 | ||
DATA PUDDING;
LENGTH FLAVOR $ 9;
INPUT FLAVOR $ SWEET RATING @@;
DATALINES;
VANILLA 1 9 VANILLA 2 8 VANILLA 3 6
VANILLA 1 7 VANILLA 2 7 VANILLA 3 5
VANILLA 1 8 VANILLA 2 8 VANILLA 3 7
VANILLA 1 7
CHOCOLATE 1 9 CHOCOLATE 2 8 CHOCOLATE 3 4
CHOCOLATE 1 9 CHOCOLATE 2 7 CHOCOLATE 3 5
CHOCOLATE 1 7 CHOCOLATE 2 6 CHOCOLATE 3 6
CHOCOLATE 1 7 CHOCOLATE 2 8 CHOCOLATE 3 4
CHOCOLATE 1 8 CHOCOLATE 3 4
;
PROC GLM DATA=PUDDING;
TITLE "Pudding Taste Evaluation";
TITLE3 "Two-way ANOVA - Unbalanced Design";
TITLE4 "---------------------------------";
CLASS FLAVOR SWEET;
MODEL RATING = FLAVOR|SWEET/SS3;*采用第三类平方和;
LSMEANS FLAVOR|SWEET/PDIFF ADJUST=TUKEY;
*LSMEANS为使用最小二乘法校正主效应平均数,
PDIFF用于计算所有配对差异的概率,
ADJUST=TUKEY是对多检验的校正;
RUN;
可以看到,只有甜度存在显著差异。
程序中加入的TITLE语句,TITLEn表示SAS输出中的第n行,TITLE和TITLE1等价。
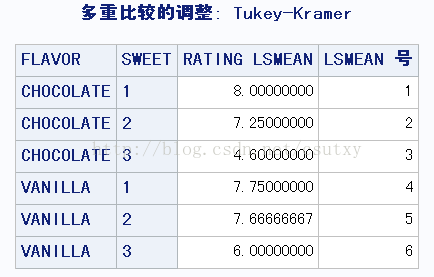
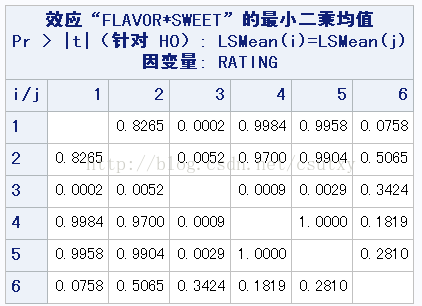
带PDIFF选项的LSMEANS语句中给出了SWEET校正后的平均数(ADJUST=TUKEY)
可以看出1对3,2对3,4对3,5对3,均显著,说明他们真的不喜欢甜巧克力。
8.协方差分析
如果有一个变量,例如IQ,影响因变量的测量,在分析因变量之前,应校正混淆 变量导致的差异。
| 组别 | |||
| A | B | ||
| 数学成绩 | IQ | 数学成绩 | IQ |
| 260 | 105 | 325 | 126 |
| 325 | 115 | 440 | 135 |
| 300 | 122 | 425 | 142 |
| 400 | 125 | 500 | 140 |
| 390 | 138 | 600 | 160 |
DATA COVAR;
LENGTH GROUP $ 1;
INPUT GROUP $ MATH IQ @@;
DATALINES;
A 260 105 A 325 115 A 300 122 A 400 125 A 390 138
B 325 126 B 440 135 B 425 142 B 500 140 B 600 160
;
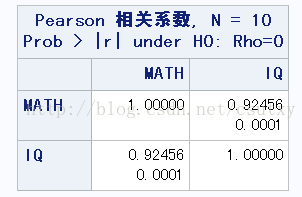
PROC CORR DATA=COVAR NOSIMPLE;
TITLE "Covariate Example";
VAR MATH IQ;
RUN;
PROC TTEST DATA=COVAR;
CLASS GROUP;
VAR MATH IQ;
RUN;
可以看到IQ和数学成绩高度相关,且各组IQ和数学成绩存在显著差异(具体输出已略)。
协方差分析之前,必须首先检验协变量和因变量的关系在不同组间的一致性,可以通过简单回归检验,在GROUP的两个水平下吧MATH作为IQ的函数纳入模型,再检验IQ和GROUP的交互作用。PROC GLM 和其中的MODEL语句可以完成建模和回归系数比较。
从结果可知IQ*GROUP无显著差异,可继续进行协方差分析:
可看到校正IQ之后,两组的数学成绩不再有显著差异。