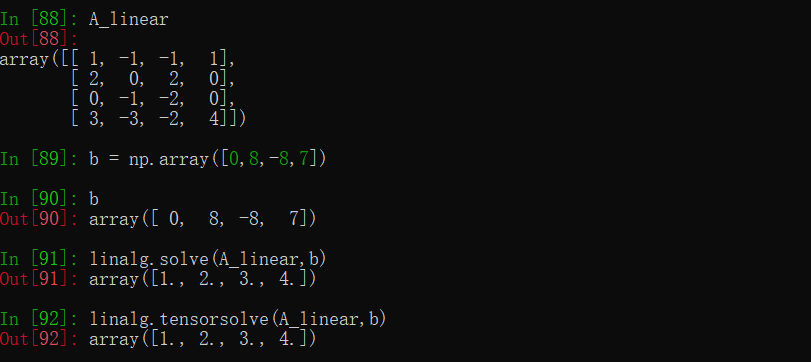利用 Numpy 进行矩阵相关运算

正文共：3266 字 31 图 预计阅读时间： 9 分钟

本文目录：

• 1. 前言
  • 1.1 基本介绍
  • 1.2 运行环境
• 2. 函数清单
• 3. 案例讲解
  • 3.1 Numpy.linalg
  • 3.2 Numpy.matlib

1.前言

1.1 基本介绍

NumPy 是Python数据分析必不可少的第三方库，NumPy 的出现一定程度上解决了Python运算性能不佳的问题，同时提供了更加精确的数据类型。如今，NumPy 被Python其它科学计算包作为基础包，已成为 Python 数据分析的基础，可以说 NumPy 就是SciPy、Pandas等数据处理或科学计算库最基本的函数功能库。

数据挖掘的理论背后，几乎离不开线性代数的计算，如矩阵乘法、矩阵分解、行列式求解等。本文将介绍 NumPy（目前最新版本为 1.16） 中与线性代数相关的模块的使用方法，包括 numpy.linalg , numpy.matlib 。

Numpy : https://docs.scipy.org/doc/numpy/reference/routines.html

numpy.linalg : https://docs.scipy.org/doc/numpy/reference/routines.linalg.html

numpy.matlib : https://docs.scipy.org/doc/numpy/reference/routines.matlib.html

numpy.dual : https://docs.scipy.org/doc/numpy/reference/routines.dual.html

numpy.fft : https://docs.scipy.org/doc/numpy/reference/routines.fft.html

（numpy.dual主要是利用scipy加速运算，用法与linalg和matlib中方法类似，这里不再多做介绍，numpy.fft涉及应用层面，限于篇幅，暂时不做扩展）

1.2 运行环境

• 操作系统： win10
• python版本：3.7.0
• IPython版本：6.5.0
• numpy版本 ：1.15.1

2.函数清单

国际惯例，引入 NumPy 使用别名 np ，所有函数清单，方便速查。另外在 Numpy 中一维数组表示向量，多维数组表示矩阵。

Linear algebra (numpy.linalg)	线性代数模块
Matrix and vector products	矩阵相乘
dot(a, b[, out])	向量或者矩阵乘积
linalg.multi_dot(arrays)	多个矩阵的乘积
vdot(a, b)	仅适用于向量内积
inner(a, b)	内积（ 对于两个二维数组的inner，相当于按X和Y的最后顺序的轴方向上取向量 ，然后依次计算内积后组成的多维数组）
outer(a, b[, out])	向量外积
matmul(x1, x2, /[, out, casting, order, …])	矩阵乘积
linalg.matrix_power(a, n)	矩阵乘幂
Decompositions	矩阵分解
linalg.qr(a[, mode])	矩阵的QR分解
linalg.svd(a[, full_matrices, compute_uv])	SVD分解
Matrix eigenvalues	特征值和特征向量
linalg.eig(a)	特征值和特征向量（方阵）
linalg.eigvals(a)	特征值（方阵）
Norms and other numbers	范数等
linalg.norm(x[, ord, axis, keepdims])	向量或者矩阵的范数
linalg.det(a)	行列式的值
linalg.matrix_rank(M[, tol, hermitian])	使用SVD分解得到矩阵的秩
trace(a[, offset, axis1, axis2, dtype, out])	迹
Solving equations and inverting matrices	解线性方程组和逆
linalg.solve(a, b)	解线性方程组的准确解（要求满秩）
linalg.tensorsolve(a, b[, axes])	解Ax=b
linalg.lstsq(a, b[, rcond])	最小二乘
linalg.inv(a)	矩阵的逆
linalg.pinv(a[, rcond])	伪逆
Matrix library (numpy.matlib)	矩阵模块
mat(data[, dtype])	矩阵类型
matrix(data[, dtype, copy])	矩阵类型
asmatrix(data[, dtype])	将输入转化为矩阵类型
bmat(obj[, ldict, gdict])	块矩阵构造
empty(shape[, dtype, order])	只记录形状的空矩阵
zeros(shape[, dtype, order])	全0矩阵
ones(shape[, dtype, order])	全1矩阵
matlib.eye(n[, M, k, dtype, order])	产生对角线元素为1，其余元素为0的矩阵。 n 行数 M列数 k 对角元相对主对角线的位置 （可以产生长矩阵）
identity(n[, dtype])	单位阵
matlib.repmat(a, m, n)	向量或矩阵（最高只支持到2维）列方向重复m次，行方向重复n次
matlib.rand(*args)	填充随机数的矩阵
matlib.randn(*args)	填充数符合标准正态分布的矩阵

3.案例讲解

3.1 numpy.linalg 模块

• 模块引入以及取别名

1import numpy as np
2import numpy.linalg as linalg

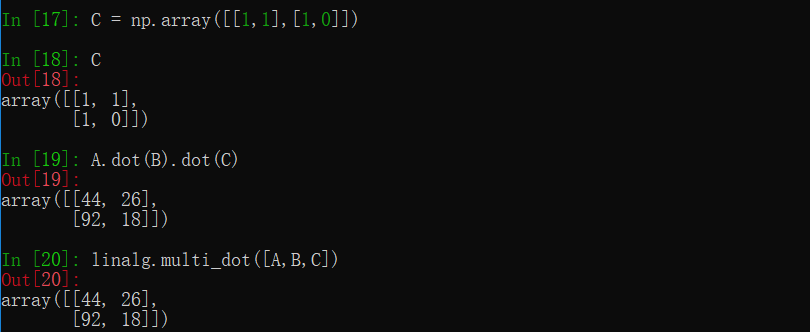
• 向量或矩阵乘积

• 多矩阵的乘积

相对于矩阵之间两两乘积，多矩阵的时候使用 multi_dot() 更加便捷

• 向量内积

只适用于向量，如果为矩阵则结果不为矩阵的内积

• 内积

# 对于两个二维数组的inner，相当于按X和Y的最后顺序的轴方向上取向量

# 然后依次计算内积后组成的多维数组

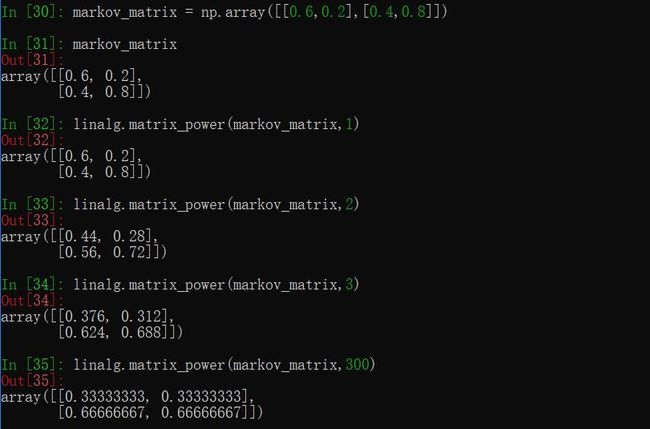
• 矩阵乘幂

这里使用第二十四讲的马尔科夫矩阵

（这里基本上已经可以确定稳态了）

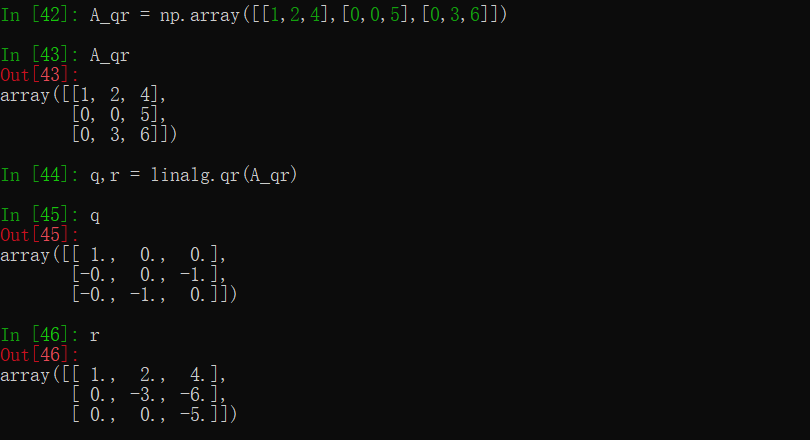
• QR分解

这里使用第十七讲习题课的矩阵，可以发现和我们之前计算的 QR 结果是一致的，只不过有符号的差别。

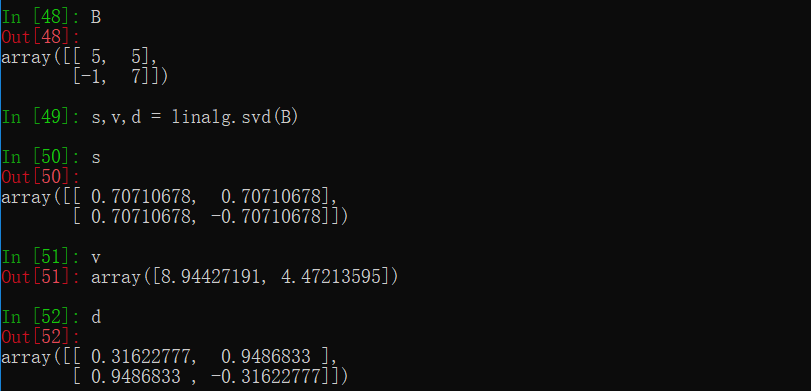
• SVD分解

这里使用第三十讲奇异值分解习题课的例子

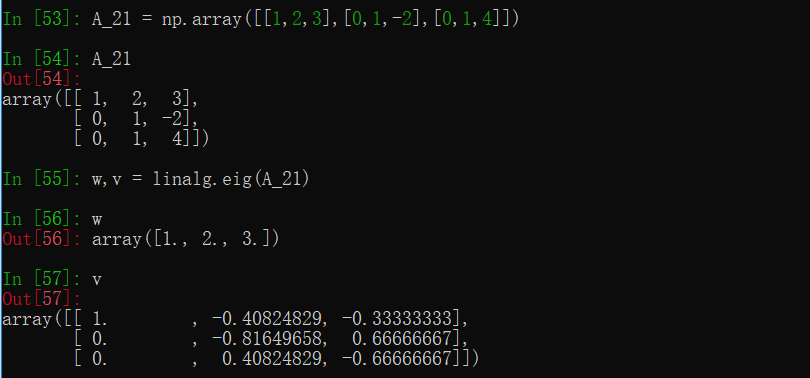
• 方阵的特征值和特征向量

这里使用第二十一讲习题课的例子

（可以发现结果都对特征向量进行了标准化）

• 特征值

该方法只返回特征值

• 范数

默认是二阶范数

• 行列式的值

可以单独求解单个矩阵的行列式的值，也可以多个矩阵同时求解行列式的值

• 矩阵的秩

同样支持多个矩阵同时求解矩阵的秩

• 矩阵的迹

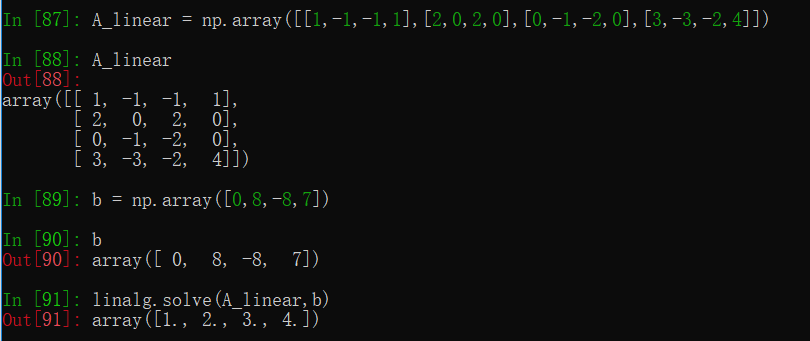
• 解线性方程组

使用第二讲矩阵消元习题的例子，该方法要求满秩，即系数矩阵为方阵且各列线性无关。

• 矩阵形式求解线性方程组 （Ax=b）

使用第二讲矩阵消元习题的例子，该方法同样要求满秩，即系数矩阵为方阵且各列线性无关。

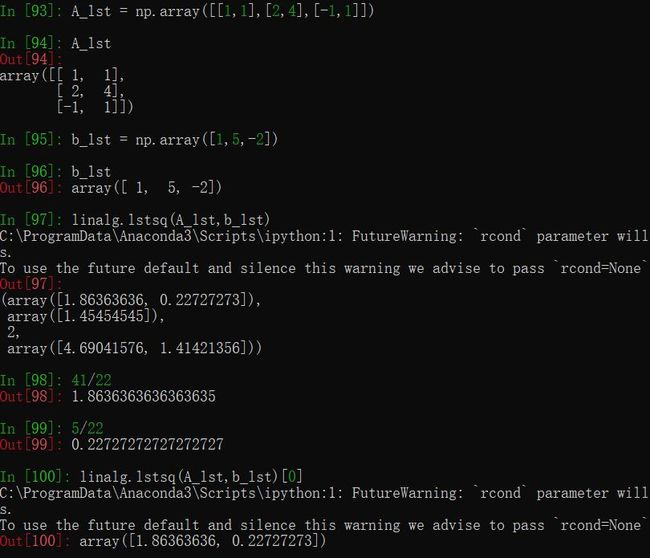
• 最小二乘

使用第十六讲习题课的例子，返回值中含有多个值，系数矩阵在返回值的第一个数组中

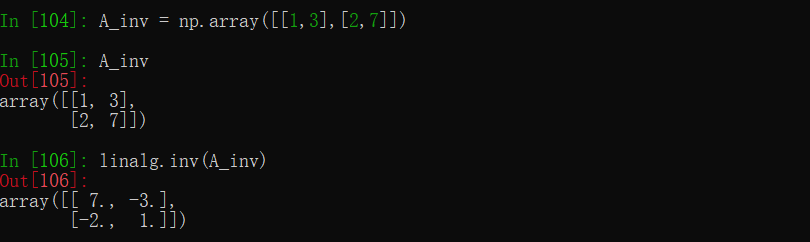
• 逆

使用第三讲课程内容中的例子

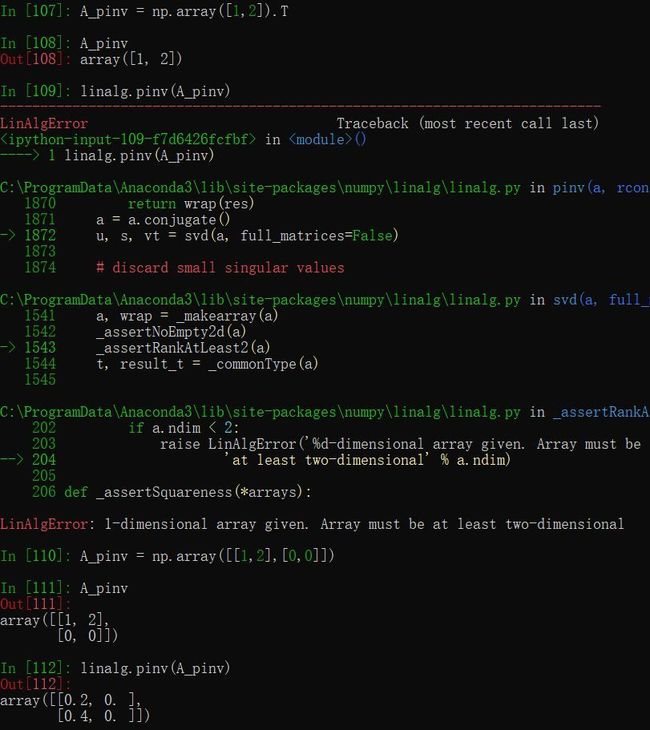
• 伪逆

使用第三十四讲习题课的例子，这里要求输入为方阵，因此使用该例子，我们将原矩阵补全为方阵

3.2 numpy.matlib 模块

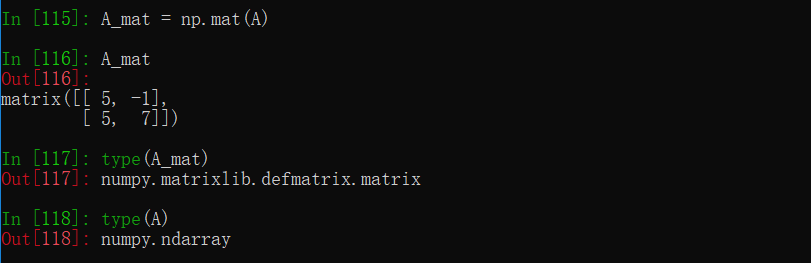
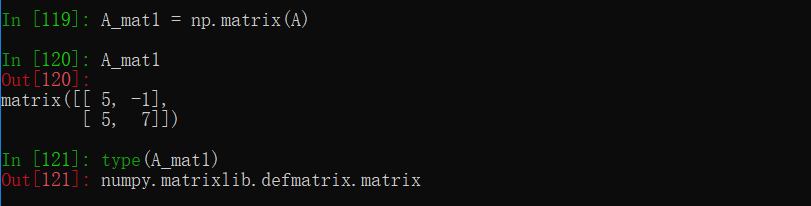
• 矩阵类型

• 将其他类型转化为矩阵类型

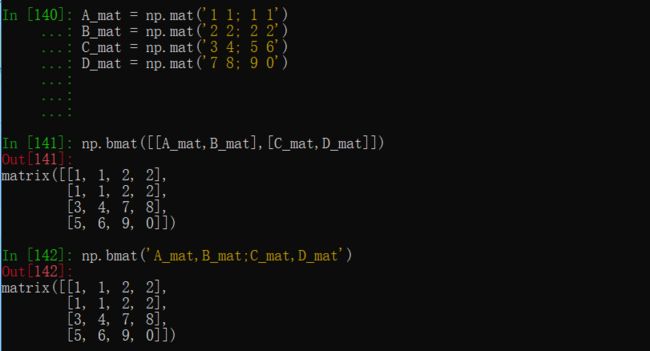
• 块矩阵构造

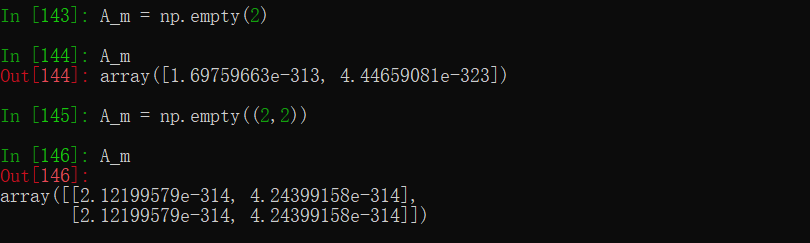
• 空矩阵

默认会填充随机值（应该是占位用的）

• 全 0 矩阵

• 全 1 矩阵

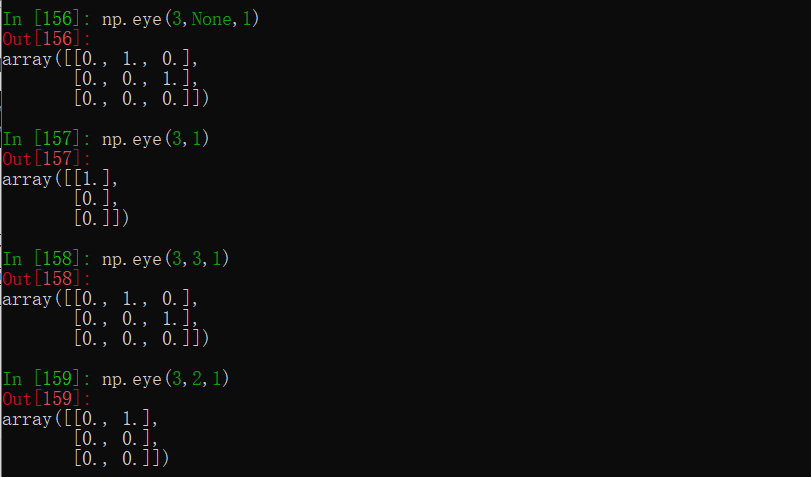
• 对角线为 1 矩阵

这里可以不止是在主对角线上，可由参数k控制，该参数定义全为 1 的对角线离主对角线的相对距离，为正则往上三角移动，为负则往下三角移动。 并且可以是非方阵。三个参数分别对应行数，列数和相对位置

• 单位阵

• 随机数矩阵

• 随机数符合标准正态分布的矩阵

原文发布于微信公众号 - 零维领域（lingweilingyu）